Беттердің дифференциалды геометриясы - Differential geometry of surfaces

Жылы математика, беттердің дифференциалды геометриясы -мен айналысады дифференциалды геометрия туралы тегіс беттер әр түрлі қосымша құрылымдармен, көбінесе, а Риман метрикасы. Беткейлер әртүрлі тұрғыдан жан-жақты зерттелген: сыртқы, оларға қатысты ендіру жылы Евклид кеңістігі және ішкі, олардың қасиеттерін бетіндегі қисықтар бойымен өлшенген беткі қашықтық арқылы ғана анықтайтын. Зерттелген негізгі ұғымдардың бірі - бұл Гаусстық қисықтық, алдымен терең зерттелген Карл Фридрих Гаусс,[1] ол қисықтықтың бетінің өзіндік қасиеті екенін көрсетті, оның эвклид кеңістігіне изометриялық енуіне тәуелсіз.
Беттер табиғи түрде пайда болады графиктер туралы функциялары жұп айнымалылар, ал кейде параметрлік түрінде немесе түрінде көрінеді локустар байланысты кеңістік қисықтары. Оларды зерттеуде маңызды рөл ойнады Өтірік топтар (рухында Эрланген бағдарламасы ), атап айтқанда симметрия топтары туралы Евклидтік жазықтық, сфера және гиперболалық жазықтық. Бұл Lie топтарын тұрақты Гаусс қисаюының беттерін сипаттауға қолдануға болады; олар сонымен қатар ішкі дифференциалды геометрияға заманауи көзқарастың маңызды ингредиентін ұсынады байланыстар. Екінші жағынан, беттің евклид кеңістігіне енуіне негізделген сыртқы қасиеттері де көп зерттелген. Бұл сызықтық емес жақсы суреттелген Эйлер-Лагранж теңдеулері ішінде вариацияларды есептеу: бірақ Эйлер түсіну үшін бір айнымалы теңдеулер жасады геодезия, ендіруге тәуелсіз анықталған, Лагранждың екі айнымалы теңдеудің негізгі қолдануларының бірі болды минималды беттер, тек ендіру тұрғысынан анықталатын тұжырымдама.
Тарих

Белгілі бір көлем квадраттық беттер туралы революция бойынша есептелген Архимед.[2] Дамуы есептеу XVII ғасырда оларды есептеудің неғұрлым жүйелі тәсілін ұсынды.[3] Жалпы беттердің қисаюын алғаш зерттеген Эйлер. 1760 жылы[4] ол беттің жазықтық кесіндісінің қисаю формуласын дәлелдеді және 1771 ж[5] ол параметрлік формада ұсынылған беттерді қарастырды. Монге өзінің теориясының негізін өзінің классикалық естелігінде қалаған L'application de l'analyse à la géometrie 1795 жылы пайда болды. Беттер теориясына анықтаушы үлес қосты Гаусс 1825 және 1827 жылдары жазылған екі керемет құжатта.[1] Бұл дәстүрден жаңаша кетуді белгіледі, өйткені Гаусс алғаш рет оны қарастырды ішкі беттің геометриясы, қасиеттері тек беткі қабаттағы евклид кеңістігінде орналасу тәсілінен тәуелсіз бетіндегі нүктелер арасындағы геодезиялық арақашықтықпен анықталады. Тәждің нәтижесі Егрегия теоремасы Гаусстың Гаусстық қисықтық ішкі инвариант, яғни локаль бойынша инвариант изометрия. Бұл көзқарас жоғары өлшемді кеңістіктерге кеңейтілді Риман және қазіргі уақытта белгілі болған нәрсеге алып келді Риман геометриясы. ХІХ ғасыр беттер теориясы үшін топологиялық тұрғыдан да, дифференциалды-геометриялық тұрғыдан да алтын ғасыр болды, көптеген жетекші геометрлер өздерін зерттеуге арнады.[дәйексөз қажет ] Дарбу өзінің төрт томдық трактатында көптеген нәтижелер жинады Théorie des беттері (1887–1896).
Шолу
Өсімдіктің жапырағы, әйнектің беті немесе бет пішіні белгілі бір жолмен қисық болады және бұл фигуралардың барлығы, тіпті қандай да бір белгілерді ескермегеннен кейін де, белгілі бір геометриялық болады деп айту интуитивті түрде таныс. бір-бірінен ерекшеленетін ерекшеліктер. Беттердің дифференциалды геометриясы осындай құбылыстарды математикалық түсінумен байланысты. 1700 жылдары заманауи түрде басталған бұл саланы зерттеу жоғары өлшемді және абстрактілі геометрияның дамуына әкелді, мысалы. Риман геометриясы және жалпы салыстырмалылық.[өзіндік зерттеу? ]
Математикалық маңызды объект - а тұрақты беті. Конвенциялар нақты анықтамасында әр түрлі болғанымен, олар үшөлшемді жиынтықтардың жалпы класын құрайды Евклид кеңістігі (ℝ3) олар «беттік» деген ұғымның бір бөлігін алады. Осындай беткейде жатқан қисықтар класын және беттердің оларды иілуге мәжбүрлейтін дәрежесін талдау арқылы ℝ3, беттің әр нүктесіне деп аталатын екі санды қосуға болады негізгі қисықтық. Олардың орташа мәні деп аталады қисықтықты білдіреді бетінің, ал олардың көбейтіндісі деп аталады Гаусстық қисықтық.
Тұрақты беттердің көптеген классикалық мысалдары бар, олардың ішінде:
- ұшақтар, цилиндрлер және сфералар сияқты таныс мысалдар
- минималды беттер, олардың қасиеттері бойынша анықталады, олардың орташа қисаюы әр нүктеде нөлге тең. Ең танымал мысалдар катеноидтар және геликоидтар, дегенмен көптеген басқалары табылды. Минималды беттерді қасиеттерімен де анықтауға болады бетінің ауданы, нәтижесінде олар формасының математикалық моделін ұсынады сабын пленкалары сым жақтауы бойынша созылған кезде
- басқарылатын беттер, бұл әр нүктеден кем дегенде бір түзу өтетін беттер; мысалдар цилиндрді және гиперболоидты бір парақтың.
Таңқаларлық нәтиже Карл Фридрих Гаусс, ретінде белгілі egregium теоремасы, анықтауы бойынша, бетіндегі қисықтардың үш өлшемді кеңістіктегі бағыттардың қалай өзгеретіндігімен байланысты болатын беттің Гаусс қисықтығы, екіге тең болғанда, беттерде жатқан қисықтардың ұзындықтарымен өлшенетіндігін көрсетті. бетіндегі қисықтар қиылысады. Терминологиялық тұрғыдан бұл Гаусс қисығын есептеуге болады деп айтады бірінші іргелі форма (деп те аталады метрикалық тензор ) бетінің. The екінші іргелі форма, керісінше, қисықтар бетінен итерілген кезде бетіндегі қисықтардың ұзындықтары мен бұрыштарының бұрмалануын кодтайтын объект.
Ұзындық пен бұрыштың әртүрлі аспектілерін өлшеуге қарамастан, бірінші және екінші негізгі формалар бір-біріне тәуелді емес және олар белгілі шектеулерді қанағаттандырады Гаусс-Кодацци теңдеулері. Жиі беттердің дифференциалды геометриясының негізгі теоремасы деп аталатын үлкен теорема Гаусс-Кодацци шектеулерін екі объект қанағаттандырған кезде олар тұрақты беттің бірінші және екінші фундаментальды формалары ретінде пайда болады деп бекітеді.
Бірінші фундаментальды форманы қолдана отырып, тұрақты бетте жаңа объектілерді анықтауға болады. Геодезия бұл белгілі бір екінші ретті қанағаттандыратын бетіндегі қисықтар қарапайым дифференциалдық теңдеу бірінші іргелі формада көрсетілген. Олар қисықтардың ұзындықтарын зерттеуге тікелей байланысты; ұзындығы жеткілікті қысқа геодезиялық әрқашан қисық болады ең қысқа оның екі соңғы нүктесін байланыстыратын бетіндегі ұзындық. Осылайша, геодезия тұрақты бетте берілген екі нүкте арасындағы ең қысқа жолды анықтайтын оңтайландыру мәселесінің негізі болып табылады.
Сондай-ақ анықтауға болады параллель тасымалдау қисықтың бір нүктесіндегі жанама векторды қисықтың басқа нүктелеріндегі жанасу векторларына бетіне жанама векторды деформациялауға арналған рецепт беретін кез келген берілген қисық бойымен. Рецепт бірінші кезекпен анықталады қарапайым дифференциалдық теңдеу бірінші іргелі формада көрсетілген.
Жоғарыда аталған тұжырымдамалардың барлығы көп айнымалы есептеулермен байланысты. The Гаусс-Бонн теоремасы бұл глобустың бетінің қисаюын топологиялық түрімен байланыстыратын неғұрлым ғаламдық нәтиже. Ол Гаусс қисығының орташа мәні толығымен анықталады деп бекітеді Эйлерге тән оның беткі қабатымен бірге беттің.
Ұғымы Риманн коллекторы және Риман беті жоғарыда қарастырылған тұрақты беттердің екі жалпылауы. Атап айтқанда, мұнда қарастырылған барлық тұрақты беттер теориясының барлығы Риман коллекторларының теориясында жалпыланған. Бұл Риман беттеріне қатысты емес, бірақ кез-келген тұрақты бет Риманның бетіне мысал келтіреді.
Евклид кеңістігіндегі тұрақты беттер
Анықтама
Шардың тегіс екендігі интуитивті түрде түсінікті, ал конус немесе пирамида олардың шыңына немесе шеттеріне байланысты болмайды. «Тұрақты бет» ұғымы тегіс бет ұғымын формализациялау болып табылады. Анықтама арасындағы карталар арқылы беттің жергілікті көрінісін пайдаланады Евклид кеңістігі. Мұндай карталар үшін тегістік туралы стандартты түсінік бар; Евклид кеңістігінің екі ашық жиыны арасындағы карта тегіс, егер оның әр ретті ішінара туындылары доменнің әр нүктесінде болса.[6][7][8]
Төменде анықтаманы ұсынудың үш баламалы әдісі келтірілген; ортаңғы анықтама, мүмкін, визуалды түрде интуитивті болып табылады, өйткені ол тұрақты беттің жиынтығы екенін айтады ℝ3 бұл тегіс функцияның графигі (бұл аймақ бойынша болсын yz ұшақ, xz ұшақ немесе xy жазықтық).

| Анықтамада қолданылатын нысандар | Евклид кеңістігіндегі тұрақты бет ℝ3 ішкі жиын болып табылады S туралы ℝ3 әрбір нүктесі S бар... |
|---|---|
| Жергілікті параметрлер | ... ашық аудан U ⊂ S ол үшін ашық ішкі жиын бар V туралы ℝ2 және а гомеоморфизм f : V → U осындай
|
| Монге патчтары | ... ашық аудан U ⊂ ℝ3 ол үшін ашық ішкі жиын бар V туралы ℝ2 және тегіс функция сағ : V → ℝ төмендегілердің бірі орындалатындай:
|
| Жасырын функциялар | ... ашық аудан U ⊂ ℝ3 ол үшін тегіс функция бар F : U → ℝ бірге:
|
Бірінші анықтамада пайда болған гомеоморфизмдер белгілі жергілікті параметрлер немесе жергілікті координаттар жүйелері немесе жергілікті диаграммалар қосулы S.[13] Алғашқы екі анықтаманың эквиваленттілігі тұрақты беттің кез-келген нүктесінің айналасында әрдайым форманың жергілікті параметрлері болатындығын дәлелдейді. (сен, v) ↦ (сағ(сен, v), сен, v), (сен, v) ↦ (сен, сағ(сен, v), v), немесе (сен, v) ↦ (сен, v, сағ(сен, v))ретінде белгілі Монге патчтары. Функциялар F үшінші анықтамада айтылғандай жергілікті анықтайтын функциялар. Барлық үш анықтаманың эквиваленттілігі келесіден шығады жасырын функция теоремасы.[14][15][16]

Кез келген екі жергілікті параметрді ескере отырып f : V → U және f ′ : V ′→ U ′ тұрақты беттің, құрамының f −1 ∘ f ′ ашық ішкі жиындары арасындағы карта ретінде міндетті түрде тегіс болады ℝ2.[17] Бұл кез-келген тұрақты беттің табиғи түрде a құрылымына ие екендігін көрсетеді тегіс коллектор, тегіс атласпен жергілікті параметрлердің кері бағыттары берілген.
Дифференциалды геометрияның классикалық теориясында беттер әдетте тек қалыпты жағдайда зерттеледі.[18][19] Сонымен қатар, екі ішінара туынды болатын тұрақты емес беттерді зерттеу жиі кездеседі ∂сен f және ∂v f жергілікті параметризация болмауы мүмкін сызықтық тәуелсіз. Бұл жағдайда, S сияқты ерекшеліктері болуы мүмкін цустальді шеттер. Мұндай беттер әдетте зерттеледі сингулярлық теориясы. Қалыпты беттердің басқа әлсіреген формалары пайда болады компьютерлік дизайн, бұл жерде беті бөлшектенген бөліктерге бөлініп, жергілікті параметрлердің туындылары шекара бойынша үзіліссіз бола бермейді.[дәйексөз қажет ]
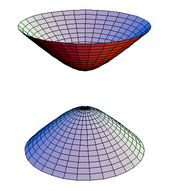
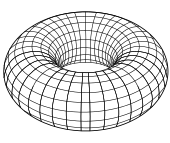

Қарапайым мысалдар. Тұрақты беттің қарапайым мысалы 2-сферада келтірілген {(х, ж, з) | х2 + ж2 + з2 = 1}; бұл бетті алты монж патчпен жабуға болады (жоғарыда келтірілген үш түрдің әрқайсысы) сағ(сен, v) = ± (1 − сен2 − v2)1/2. Сонымен бірге оны екі жергілікті параметрмен қамтуға болады стереографиялық проекция. Жинақ {(х, ж, з) : ((х2 + ж2)1/2 − р)2 + з2 = R2} Бұл революция торы радиусымен р және R. Бұл тұрақты бет; формуланың жергілікті параметрлері берілуі мүмкін
The гиперболоидты екі параққа {(х, ж, з) : з2 = 1 + х2 + ж2} - тұрақты бет; оны екі монж патчымен жабуға болады сағ(сен, v) = ±(1 + сен2 + v2)1/2. The геликоид теориясында кездеседі минималды беттер. Ол бір ғана жергілікті параметризациямен қамтылған, f(сен, v) = (сен күнә v, сен cos v, v).
Тангенс векторлары және қалыпты векторлар
Келіңіздер S тұрақты беті болыңыз ℝ3және рұқсат етіңіз б элементі болу S. Жоғарыда аталған анықтамалардың кез-келгенін пайдаланып, векторларды бөліп көрсетуге болады ℝ3 тангенс ретінде S кезінде б, және белгілі бір векторлар ℝ3 ретінде ортогоналды ретінде S кезінде б.
| Анықтамада қолданылатын нысандар | Вектор X жылы ℝ3 жанасады S кезінде б егер ... | Вектор n жылы ℝ3 бұл қалыпты жағдай S кезінде б егер ... |
|---|---|---|
| Жергілікті параметрлер | ... кез-келген жергілікті параметрлеу берілген f : V → S бірге б ∈ f(V), X -ның сызықтық комбинациясы болып табылады және | ... ол әрбір жанама векторға ортогоналды S кезінде б |
| Монге патчтары | ... кез-келген монж патчына арналған (сен, v) ↦ (сен, v, сағ(сен, v)) оның ауқымы кіреді б, біреуінде бар нүктеде бағаланатын ішінара туындылармен (б1, б2). Ұқсас анықтама басқа екі формадағы монж патчтары жағдайында қолданылады. | ... кез-келген монж патчына арналған (сен, v) ↦ (сен, v, сағ(сен, v)) оның ауқымы кіреді б, n -ның еселігі (∂сағ/∂сен, ∂сағ/∂v, −1) нүктесінде бағаланғандай (б1, б2). Ұқсас анықтама басқа екі формадағы монж патчтары жағдайында қолданылады. |
| Жасырын функциялар | ... кез-келген жергілікті анықтайтын функция үшін F оның домені бар б, X ортогоналды болып табылады ∇F(б) | ... кез-келген жергілікті анықтайтын функция үшін F оның домені бар б, n -ның еселігі ∇F(б) |
Біреуі көреді жанасу кеңістігі дейін S кезінде б, ол барлық жанама векторлардан тұратын анықталған S кезінде б, - бұл екі өлшемді сызықтық ішкі кеңістік ℝ3; оны жиі белгілейді ТбS. The қалыпты кеңістік дейін S кезінде б, ол барлық векторлардан тұратын анықталған S кезінде б, - бұл бір өлшемді сызықтық ішкі кеңістік ℝ3 жанасатын кеңістікке ортогоналды болып табылады ТбS. Осылайша, әр сәтте б туралы S, деп аталады бірлік ұзындығының екі қалыпты векторы бірлік қалыпты векторлар. Бірліктің қалыпты векторларын атап өткен жөн б формулалар арқылы жергілікті параметрлер, монге патчтары немесе жергілікті анықтайтын функциялар тұрғысынан берілуі мүмкін
алдыңғы анықтамалардағыдай белгілерді орындау.
Тангенс векторларының «меншікті» анықтамасын атап өткен жөн, бұл тұрақты беттік теорияны жалпылауға тән болып табылады. тегіс коллекторлар. Ол жанас кеңістігін сызықтық ішкі кеңістік ретінде емес, дерексіз екі өлшемді нақты векторлық кеңістік ретінде анықтайды. ℝ3. Бұл анықтамада жанама вектор дейді S кезінде б әрбір жергілікті параметрге арналған тапсырма f : V → S бірге б ∈ f(V), екі саннан X1 және X2, кез келген басқа жергілікті параметрлеу үшін f ′ : V → S бірге б ∈ f(V) (және сәйкес сандармен (X ′)1 және (X ′)2), біреуінде бар
қайда Af ′(б) болып табылады Якоб матрицасы картаға түсіру f −1 ∘ f ′, нүктесінде бағаланады f ′(б). Жанасу векторларының жиынтығы S кезінде б табиғи түрде екі өлшемді векторлық кеңістіктің құрылымына ие. Тангенс векторы осы мағынадағы векторды қарастыру арқылы алдыңғы мағынасындағы тангенс векторына сәйкес келеді
жылы ℝ3. Якобиандық шарт X1 және X2 қамтамасыз етеді тізбек ережесі, бұл вектор тәуелді емес f.
Беттегі тегіс функциялар үшін векторлық өрістер (яғни жанамалы векторлық өрістер) бірінші реттік операторлар немесе туындылар ретінде маңызды интерпретацияға ие. Келіңіздер тұрақты беткей болыңыз, жазықтықтың ашық ішкі бөлігі және координаттар кестесі. Егер , кеңістік көмегімен анықтауға болады . Сол сияқты векторлық өрістерді анықтайды векторлық өрістер қосылған . Стандартты айнымалыларды қабылдау сен және v, векторлық өрістің формасы болады , бірге а және б тегіс функциялар. Егер бұл векторлық өріс және тегіс функция болып табылады сонымен қатар тегіс функция. Бірінші ретті дифференциалдық оператор Бұл туынды, яғни ол Лейбниц ережесін қанағаттандырады [20]
Векторлық өрістер үшін X және Y оператор екенін тексеру оңай - векторлық өріске сәйкес келетін туынды. Ол деп аталады Жалған жақша . Бұл қисық-симметриялы және Якоби сәйкестігін қанағаттандырады:
Қорытындыда векторлық өрістер қосулы немесе а Алгебра Өтірік кронштейнінің астында.[21]
Бірінші және екінші негізгі формалар, пішін операторы және қисықтық
Келіңіздер S тұрақты беті болыңыз ℝ3. Жергілікті параметрлеу берілген f : V → S және векторлық қалыпты векторлық өріс n дейін f(V), келесі объектілерді нақты немесе матрицалық функциялар ретінде анықтайды V. Бірінші іргелі форма тек тәуелді f, және емес n. Төртінші бағанда осы функциялардың тәуелділігі жазылады f, функцияларын байланыстыру арқылы E ′, F ′, G ′, L ′, т.б. жергілікті параметрлеуді таңдау үшін туындайтын және т.б. f ′ : V ′ → S, туындайтындарға f. Мұнда A дегенді білдіреді Якоб матрицасы туралы f –1 ∘ f ′. Төртінші бағанның формулаларын құрудағы негізгі қатынас сол кезде болады
келесідей тізбек ережесі.
| Терминология | Ескерту | Анықтама | Жергілікті параметрлеуге тәуелділік |
|---|---|---|---|
| Бірінші іргелі форма | E | ||
| F | |||
| G | |||
| Екінші іргелі форма | L | ||
| М | |||
| N | |||
| Пішін операторы[22] | P | ||
| Гаусстық қисықтық | Қ | ||
| Орташа қисықтық | H | ||
| Негізгі қисықтықтар |
Фигура операторын анықтайтын матрицамен тікелей есептеулер арқылы Гаусс қисықтығының анықтауыш фигура операторының орташа қисаюы болып табылады із фигура операторының, ал негізгі қисықтықтар болып табылады меншікті мәндер форма операторының; сонымен қатар, Гаусс қисығы негізгі қисықтықтардың көбейтіндісі, ал орташа қисықтық олардың қосындысы болып табылады. Бұл бақылауларды осы объектілердің анықтамалары ретінде де тұжырымдауға болады. Бұл бақылаулар сонымен қатар төртінші бағанның соңғы үш жолы алдыңғы қатардан дереу ілесетінін анық көрсетеді ұқсас матрицалар бірдей детерминант, із және өзіндік мәндерге ие. Айта кету керек E, G, және EG − F2 барлығы міндетті түрде оң. Бұл форма операторын анықтауда кері матрицаның нақты анықталуын және негізгі қисықтықтардың нақты сандар болуын қамтамасыз етеді.
Қалыпты векторлық өрісті таңдауды жоққа шығару екінші фундаментальды форманы, форма операторын, орташа қисықтықты және негізгі қисықтықтарды жоққа шығарады, бірақ Гаусс қисығын өзгеріссіз қалдырады. Қысқаша айтқанда, бұл қалыпты бетті ескере отырып, мұны көрсетті S, Гаусс қисығы S бойынша нақты бағаланатын функция ретінде қарастыруға болады S; барлығына қалыпты векторлық өрісті таңдауға қатысты S, екі негізгі қисықтық және орташа қисықтық сонымен қатар нақты мәнге ие функциялар болып табылады S.
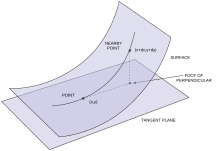

Геометриялық тұрғыдан бірінші және екінші фундаментальды формалар қалай ақпарат беретіні ретінде қарастырылуы мүмкін f(сен, v) ішіне қозғалады ℝ3 сияқты (сен, v) ішіне қозғалады V. Атап айтқанда, бірінші іргелі форма қаншалықты тез кодталады f қозғалады, ал екінші фундаменталь формасы оның қозғалысы қалыпты вектор бағытында қаншалықты болатындығын кодтайды n. Басқа сөзбен айтқанда, екінші іргелі форма б бастап ортогональ проекциясының ұзындығын кодтайды S жанама жазықтыққа S кезінде б; атап айтқанда, бұл осы ұзындыққа жақындататын квадраттық функцияны береді. Бұл ойлауды формулалар арқылы дәл жасауға болады
тікелей анықтамаларынан туындайтын негізгі формалардың және Тейлор теоремасы екі өлшемде. Негізгі қисықтықтарды келесі түрде қарастыруға болады. Берілген сәтте б туралы S, ортогональ сызығы бар барлық жазықтықтардың жиынтығын қарастырайық S. Әрбір осындай жазықтықтың қиылысу қисығы бар Sдеп қарастыруға болады жазықтық қисығы ұшақтың ішінде. Екі негізгі қисықтық б - осы жазықтық қисығының қисаюының максималды және минималды мәндері б, қарастырылып отырған жазықтық қалыпты сызықтың айналасында болғандықтан.
Монге патчына қатысты жоғарыда көрсетілген шамалардың есебі төменде келтірілген f(сен, v) = (сен, v, сағ(сен, v)). Мұнда сағсен және сағv екі ішінара туындысын белгілеңіз сағ, екінші ішінара туындыларға арналған ұқсас белгілермен. Екінші фундаментальды форма және одан кейінгі барлық шамалар берілген бірліктің қалыпты векторлық өрісіне қатысты есептеледі.
| Саны | Формула |
|---|---|
| Қалыпты векторлық өріс | |
| Бірінші іргелі форма | |
| Екінші іргелі форма | |
| Пішін операторы | |
| Гаусстық қисықтық | |
| Орташа қисықтық |
Кристоффель символдары, Гаусс-Кодацци теңдеулері және Теорема Эгрегия
Келіңіздер S тұрақты беті болыңыз ℝ3. The Christoffel рәміздері тағайындау, әрбір жергілікті параметрлерге f : V → S, сегіз функция қосулы V, арқылы анықталады[23]
Оларды келесі формулалармен анықтауға болады, онда n - бойымен бірлік қалыпты векторлық өріс f(V) және L, М, N екінші іргелі форманың сәйкес компоненттері:
Бұл анықтаманың кілті мынада ∂f/∂сен, ∂f/∂v, және n негізін құрайды ℝ3 үш нүктенің әрқайсысы Кристоффель символдарын екінші дербес туындыларының координаталары ретінде ерекше көрсететін әр нүктеде f. Қалыпты бірлікті таңдау Christoffel рәміздеріне әсер етпейді, өйткені, егер n оны теріске шығаруға ауыстырылады, содан кейін екінші фундаментальды форманың компоненттері де жоққа шығарылады, сондықтан Ln, Мн, Nn өзгеріссіз қалады.
Екінші анықтама жергілікті параметрлеу аясында Кристоффель символдарының геометриялық табиғи екендігін көрсетеді. Бірінші анықтамадағы формулалар аз табиғи болып көрінгенімен, олар Кристоффель символдарын екінші анықтамадан бірден байқалмайтын бірінші іргелі формадан есептеуге болатындығын көрсету маңызды. Анықтамалардың эквиваленттілігін бірінші анықтаманы екіншісіне тікелей ауыстыру арқылы анықтауға болады. E, F, G.
The Кодацци теңдеулері дәлелде[24]
Бұл теңдеулерді жоғарыда келтірілген Христофель символдарының екінші анықтамасынан тікелей алуға болады; мысалы, бірінші Кодацци теңдеуі бірінші теңдеуді қатысты дифференциалдау арқылы алынады v, қатысты екінші теңдеу сен, екеуін алып тастап, нүктелік өнімді бірге алыңыз n. The Гаусс теңдеуі деп бекітеді[25]
Оларды Codazzi теңдеулері сияқты шығаруға болады, олардың біреуін Вайнартен теңдеулері нүктелік өнімді алудың орнына n. Бұл үш бөлек теңдеу түрінде жазылғанымен, олар бірінші фундаментальды формада Кристоффель символдарының анықтамаларын ауыстырған кезде бірдей болады. Алынған өрнекті жазудың көптеген тәсілдері бар, олардың бірі 1852 ж. Бриоски анықтауыштарды шебер қолдана отырып:[26][27]
Кристоффель рәміздері бірінші фундаментальды формамен анықталған деп саналғанда, Гаусс және Кодацци теңдеулері бірінші және екінші фундаментальды формалар арасындағы белгілі бір шектеулерді білдіреді. Гаусс теңдеуі ерекше назар аударады, өйткені ол Гаусс қисықтығын бірінші кезектегі формадан басқа ақпарат қажет етпей-ақ есептеуге болатындығын көрсетеді; баламалы, бұл айтады LN − М2 функциясы ретінде жазылуы мүмкін E, F, G, жеке компоненттер болса да L, М, N мүмкін емес. Бұл белгілі egregium теоремасы, және бұл үлкен жаңалық болды Карл Фридрих Гаусс. Гаусс қисығының геометриялық анықтамасын еске түсіргенде ерекше әсер қалдырады S осцуляциялық шеңберлердің максималды және минималды радиустарымен анықталғандай; олар қалай геометриямен түбегейлі анықталған сияқты S ішінде иілу ℝ3. Осыған қарамастан, теорема олардың көбейтіндісін «меншікті» геометриядан анықтауға болатындығын көрсетеді S, тек қисықтардың ұзындықтарымен байланысты S және олардың қиылысында пайда болған бұрыштар. Айтқандай Марсель Бергер:[28]
Бұл теорема таң қалдырады. [...] Бұл басқа математик ашқанға дейін ондаған жылдар күте алатын теореманың түрі, өйткені интеллектуалды тарихтың көп бөлігінен айырмашылығы ол ауада болған жоқ. [...] Біздің білуімізше, бүгінде эгрегия теоремасының қарапайым геометриялық дәлелі жоқ.
Гаусс-Кодацци теңдеулері де болуы мүмкін қысқаша айтылған және алынған тілінде байланыс формалары байланысты Эли Картан.[29] Тілінде тензор есебі, табиғи көрсеткіштер мен қосылыстарды пайдалану тензор байламы, Гаусс теңдеуін келесі түрде жазуға болады H2 − |сағ|2 = R және екі Кодацци теңдеуін келесі түрде жазуға болады ∇1 сағ12 = ∇2 сағ11 және ∇1 сағ22 = ∇2 сағ12; Christoffel рәміздеріне қатысты күрделі өрнектер және бірінші негізгі формасы ковариантты тензор туындысының анықтамаларына толығымен енеді ∇сағ және скалярлық қисықтық R. Пьер Боннет Гаусс-Кодацци теңдеулерін қанағаттандыратын екі квадраттық форма әрқашан енгізілген бетті жергілікті деңгейде анықтайтындығын дәлелдеді.[30] Осы себепті Гаусс-Кодацци теңдеулерін ішкі және сыртқы қисықтықтардың қайдан шығатынын дәл анықтап, ендірілген беттерге арналған негізгі теңдеулер деп атайды. Олар жалпыланған беттерге жалпылауды қабылдайды Риман коллекторлары.
Изометриялар
Диффеоморфизм ашық жиынтықтар арасында және тұрақты бетте деп аталады изометрия егер ол метриканы сақтаса, яғни бірінші іргелі форма.[31][32][33] Осылайша әрбір нүкте үшін жылы жанасу векторлары кезінде , теңдіктер бар
Бірінші іргелі формадан шыққан ішкі өнім тұрғысынан мұны келесі түрде жазуға болады
- .

Екінші жағынан, параметрленген қисықтың ұзындығы деп есептеуге болады
және егер қисық жатса , айнымалылардың өзгеру ережелері мұны көрсетеді
Керісінше болса барлық қисықтардағы ұзындықты сақтайды изометрия болып табылады. Шындығында да , жанама векторлар және жанама векторларды беріңіз және . Тангенс векторларын таңдау үшін теңдіктер орындалуы керек және Сонымен қатар және , сондай-ақ .[34]
Изометрияның қарапайым мысалы екі параметрлеу арқылы келтірілген және ашық жиынтық қалыпты беттерге және . Егер , және , содан кейін изометриясы болып табылады үстінде .[35]
Цилиндр мен жазықтық локальды изометриялық, бірақ топологиялық себептерге байланысты изометрияға дейін кеңейтілмейтін беттерге мысалдар келтіреді.[36] Тағы бір мысал ретінде катеноид және геликоид жергілікті изометриялық болып табылады.[37]
Ковариант туындылары
Бұл бөлім жоқ сілтеме кез келген ақпарат көздері. (Тамыз 2020) (Бұл шаблон хабарламасын қалай және қашан жою керектігін біліп алыңыз) |
A тангенциалды векторлық өріс X қосулы S тағайындайды, әрқайсысына б жылы Sтангенс векторы Xб дейін S кезінде б. Тангенс векторларының «ішкі» анықтамасына сәйкес, тангенциалды векторлық өріс X содан кейін әрбір жергілікті параметрлерге тағайындайды f : V → S, екі нақты функция X1 және X2 қосулы V, сондай-ақ
әрқайсысы үшін б жылы S. Біреуі айтады X егер функциялар тегіс болса X1 және X2 кез-келген таңдау үшін тегіс f.[38] Тангенс векторларының жоғарыда келтірілген басқа анықтамаларына сәйкес, тангенциалды векторлық өрісті де қарастыруға болады X қосулы S карта ретінде X : S → ℝ3 осындай X(б) жанасу кеңістігінде орналасқан ТбS ⊂ ℝ3 әрқайсысы үшін б жылы S. Жалпы жағдайда жиі кездеседі тегіс коллекторлар, тангенциалды векторлық өрістер анықтауға болады тегіс функциялар кеңістігіндегі белгілі дифференциалдық операторлар ретінде S.
The ковариант туындылары («тангенциалдық туындылар» деп те аталады) of Туллио Леви-Сивита және Грегорио Риччи-Кербастро тегіс тангенциалды векторлық өрістерді саралау құралымен қамтамасыз ету. Тангенциалды векторлық өріс берілген X жанама вектор Y дейін S кезінде б, ковариант туынды ∇YX - белгілі бір жанама вектор S кезінде б. Демек, егер X және Y екеуі де тангенциалды векторлық өрістер болып табылады ∇YX тангенциалды векторлық өріс ретінде қарастыруға болады; итеративті, егер X, Y, және З тангенциалды векторлық өрістер, оларды есептеуге болады ∇З∇YX, бұл тағы бір тангенциалды векторлық өріс болады. Ковариант туындысын анықтаудың бірнеше әдісі бар; Төменде Christoffel таңбалары және тангенс векторларының «ішкі» анықтамасы қолданылады, ал екіншісі геометриялық түрде айқынырақ болады.
Тангенциалды векторлық өріс берілген X жанама вектор Y дейін S кезінде б, біреуін анықтайды ∇YX жанама вектор болу керек б which assigns to a local parametrization f : V → S the two numbers
қайда Д.(Y1, Y2) болып табылады бағытталған туынды.[39] This is often abbreviated in the less cumbersome form (∇YX)к = ∂Y(X к) + Y менΓк
ижX j, пайдалану Эйнштейн жазбасы and with the locations of function evaluation being implicitly understood. This follows a standard prescription жылы Риман геометриясы for obtaining a байланыс а Риман метрикасы. It is a fundamental fact that the vector
жылы ℝ3 is independent of the choice of local parametization f, although this is rather tedious to check.
One can also define the covariant derivative by the following geometric approach, which does not make use of Christoffel symbols or local parametrizations.[40][41][42] Келіңіздер X векторлық өріс болыңыз S, viewed as a function S → ℝ3. Given any curve c : (а, б) → S, one may consider the composition X ∘ c : (а, б) → ℝ3. As a map between Euclidean spaces, it can be differentiated at any input value to get an element (X ∘ c)′(т) туралы ℝ3. The ортогональды проекция of this vector onto Тc(т)S defines the covariant derivative ∇c ′(т)X. Although this is a very geometrically clean definition, it is necessary to show that the result only depends on c′(т) және X, and not on c және X; local parametrizations can be used for this small technical argument.
It is not immediately apparent from the second definition that covariant differentiation depends only on the first fundamental form of S; however, this is immediate from the first definition, since the Christoffel symbols can be defined directly from the first fundamental form. It is straightforward to check that the two definitions are equivalent. The key is that when one regards X1∂f/∂сен + X2∂f/∂v сияқты ℝ3-valued function, its differentiation along a curve results in second partial derivatives ∂2f; the Christoffel symbols enter with orthogonal projection to the tangent space, due to the formulation of the Christoffel symbols as the tangential components of the second derivatives of f негізге қатысты ∂f/∂сен, ∂f/∂v, n.[43] This is discussed in the above section.
The right-hand side of the three Gauss equations can be expressed using covariant differentiation. For instance, the right-hand side
can be recognized as the second coordinate of
негізге қатысты ∂f/∂сен, ∂f/∂v, as can be directly verified using the definition of covariant differentiation by Christoffel symbols. Тілінде Риман геометриясы, this observation can also be phrased as saying that the right-hand sides of the Gauss equations are various components of the Ricci қисықтығы туралы Levi-Civita байланысы of the first fundamental form, when interpreted as a Риман метрикасы.
Мысалдар

Surfaces of revolution
A surface of revolution is obtained by rotating a curve in the xz-plane about the з-аксис. Such surfaces include spheres, cylinders, cones, tori, and the катеноид. Генерал ellipsoids, hyperboloids, және параболоидтар емес. Suppose that the curve is parametrized by
бірге с drawn from an interval (а, б). Егер c1 is never zero, if c1′ және c2′ are never both equal to zero, and if c1 және c2 are both smooth, then the corresponding surface of revolution
will be a regular surface in ℝ3. A local parametrization f : (а, б) × (0, 2π) → S арқылы беріледі
Relative to this parametrization, the geometric data is:[44]
| Саны | Формула |
|---|---|
| A unit normal vector field | |
| Бірінші іргелі форма | |
| Екінші іргелі форма | |
| Негізгі қисықтықтар | |
| Гаусстық қисықтық | |
| Орташа қисықтық |
In the special case that the original curve is parametrized by arclength, i.e. (c1′(с))2 + (c1′(с))2 = 1, one can differentiate to find c1′(с)c1′′(с) + c2′(с)c2′′(с) = 0. On substitution into the Gaussian curvature, one has the simplified
The simplicity of this formula makes it particularly easy to study the class of rotationally symmetric surfaces with constant Gaussian curvature.[45] By reduction to the alternative case that c2(s) = s, one can study the rotationally symmetric minimal surfaces, with the result that any such surface is part of a plane or a scaled catenoid.[46]
Each constant-т curve on S can be parametrized as a geodesic; a constant-с curve on S can be parametrized as a geodesic if and only if c1′(s) нөлге тең. Generally, geodesics on S арқылы басқарылады Clairaut's relation.

Квадраттық беттер
Consider the quadric surface defined by[47]
This surface admits a parametrization
The Gaussian curvature and mean curvature are given by

Ruled surfaces
A ruled surface is one which can be generated by the motion of a straight line in E3.[48] A таңдау директрица on the surface, i.e. a smooth unit speed curve c(т) orthogonal to the straight lines, and then choosing сен(т) to be unit vectors along the curve in the direction of the lines, the velocity vector v = cт және сен қанағаттандыру
The surface consists of points
сияқты с және т әр түрлі.
Содан кейін, егер
the Gaussian and mean curvature are given by
The Gaussian curvature of the ruled surface vanishes if and only if сент және v are proportional,[49] This condition is equivalent to the surface being the конверт of the planes along the curve containing the tangent vector v and the orthogonal vector сен, i.e. to the surface being дамытылатын along the curve.[50] More generally a surface in E3 has vanishing Gaussian curvature near a point if and only if it is developable near that point.[51] (An equivalent condition is given below in terms of the metric.)
Минималды беттер
1760 жылы Лагранж extended Euler's results on the вариацияларды есептеу involving integrals in one variable to two variables.[52] He had in mind the following problem:
Given a closed curve in E3, find a surface having the curve as boundary with minimal area.
Such a surface is called a минималды беті.
1776 жылы Жан Батист Меуснье showed that the differential equation derived by Lagrange was equivalent to the vanishing of the mean curvature of the surface:
A surface is minimal if and only if its mean curvature vanishes.
Minimal surfaces have a simple interpretation in real life: they are the shape a soap film will assume if a wire frame shaped like the curve is dipped into a soap solution and then carefully lifted out. The question as to whether a minimal surface with given boundary exists is called Plateau's problem after the Belgian physicist Джозеф платосы who carried out experiments on soap films in the mid-nineteenth century. 1930 жылы Джесси Дуглас және Тибор Радо gave an affirmative answer to Plateau's problem (Douglas was awarded one of the first Fields medals for this work in 1936).[53]
Many explicit examples of minimal surface are known explicitly, such as the катеноид, геликоид, Шерк беті және Эннепер беті. There has been extensive research in this area, summarised in Osserman (2002). In particular a result of Osserman shows that if a minimal surface is non-planar, then its image under the Gauss map is dense in S2.

Surfaces of constant Gaussian curvature

If a surface has constant Gaussian curvature, it is called a surface of constant curvature.[54]
- Қондырғы сфера жылы E3 has constant Gaussian curvature +1.
- Евклид ұшақ және цилиндр both have constant Gaussian curvature 0.
- The surfaces of revolution with φтт = φ have constant Gaussian curvature –1. Particular cases are obtained by taking φ(т) =C қош т, C синх т және C eт.[55] The latter case is the classical жалған атмосфера generated by rotating a трактрикс орталық осьтің айналасында. 1868 жылы Евгенио Белтрами showed that the geometry of the pseudosphere was directly related to that of the гиперболалық жазықтық арқылы дербес ашылды Лобачевский (1830) және Боляй (1832). Already in 1840, F. Minding, a student of Gauss, had obtained trigonometric formulas for the pseudosphere identical to those for the hyperbolic plane.[56] The intrinsic geometry of this surface is now better understood in terms of the Poincaré metric үстінде жоғарғы жарты жазықтық немесе диск дискі, and has been described by other models such as the Klein model немесе гиперболоидтық модель, obtained by considering the two-sheeted hyperboloid q(х, ж, з) = −1 үш өлшемді Минковский кеңістігі, қайда q(х, ж, з) = х2 + ж2 – з2.[57]
Each of these surfaces of constant curvature has a өтпелі Өтірік тобы of symmetries. This group theoretic fact has far-reaching consequences, all the more remarkable because of the central role these special surfaces play in the geometry of surfaces, due to Пуанкаре Келіңіздер теңдестіру теоремасы (төменде қараңыз).
Other examples of surfaces with Gaussian curvature 0 include конустар, tangent developables, and more generally any developable surface.
Local metric structure
For any surface embedded in Euclidean space of dimension 3 or higher, it is possible to measure the length of a curve on the surface, the angle between two curves and the area of a region on the surface. This structure is encoded infinitesimally in a Риман метрикасы on the surface through line elements және area elements. Classically in the nineteenth and early twentieth centuries only surfaces embedded in R3 were considered and the metric was given as a 2×2 оң анықталған матрица varying smoothly from point to point in a local parametrization of the surface. The idea of local parametrization and change of coordinate was later formalized through the current abstract notion of a көпжақты, a topological space where the тегіс құрылым is given by local charts on the manifold, exactly as the planet Earth is mapped by атластар бүгін. Changes of coordinates between different charts of the same region are required to be smooth. Just as contour lines on real-life maps encode changes in elevation, taking into account local distortions of the Earth's surface to calculate true distances, so the Riemannian metric describes distances and areas "in the small" in each local chart. In each local chart a Riemannian metric is given by smoothly assigning a 2×2 positive definite matrix to each point; when a different chart is taken, the matrix is transformed according to the Якоб матрицасы координатаның өзгеруі. The manifold then has the structure of a 2-dimensional Риманн коллекторы.
Пішін операторы

The дифференциалды дн туралы Гаусс картасы n can be used to define a type of extrinsic curvature, known as the форма операторы[58] немесе Вайнартен карта. This operator first appeared implicitly in the work of Wilhelm Blaschke and later explicitly in a treatise by Burali-Forti and Burgati.[59] Since at each point х of the surface, the tangent space is an ішкі өнім кеңістігі, the shape operator Sх can be defined as a linear operator on this space by the formula
for tangent vectors v, w (the inner product makes sense because дн(v) және w both lie in E3).[a] The right hand side is symmetric in v және w, so the shape operator is өзін-өзі біріктіру жанасу кеңістігінде. Меншікті мәндері Sх are just the principal curvatures к1 және к2 кезінде х. Атап айтқанда анықтауыш of the shape operator at a point is the Gaussian curvature, but it also contains other information, since the mean curvature жартысы із of the shape operator. The mean curvature is an extrinsic invariant. In intrinsic geometry, a cylinder is developable, meaning that every piece of it is intrinsically indistinguishable from a piece of a plane since its Gauss curvature vanishes identically. Its mean curvature is not zero, though; hence extrinsically it is different from a plane.
Equivalently, the shape operator can be defined as a linear operator on tangent spaces, Sб: ТбМ→ТбМ. Егер n is a unit normal field to М және v is a tangent vector then
(there is no standard agreement whether to use + or − in the definition).
Жалпы, меншікті векторлар және меншікті мәндер of the shape operator at each point determine the directions in which the surface bends at each point. The eigenvalues correspond to the principal curvatures of the surface and the eigenvectors are the corresponding principal directions. The principal directions specify the directions that a curve embedded in the surface must travel to have maximum and minimum curvature, these being given by the principal curvatures.
Geodesic curves on a surface
Curves on a surface which minimize length between the endpoints are called геодезия; they are the shape that an elastic band stretched between the two points would take. Mathematically they are described using қарапайым дифференциалдық теңдеулер және вариацияларды есептеу. The differential geometry of surfaces revolves around the study of geodesics. It is still an open question whether every Riemannian metric on a 2-dimensional local chart arises from an embedding in 3-dimensional Euclidean space: the theory of geodesics has been used to show this is true in the important case when the components of the metric are аналитикалық.
Геодезия
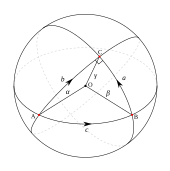
Given a piecewise smooth path c(т) = (х(т), ж(т)) in the chart for т жылы [а, б], оның ұзындығы арқылы анықталады
және энергия арқылы
Ұзындық жолдың параметрленуіне тәуелді емес. Бойынша Эйлер-Лагранж теңдеулері, егер c(т) бұл ұзындықты азайту жолы, ұзындығы бойынша параметрленген, ол қанағаттандыруы керек Эйлер теңдеулері
қайда Christoffel рәміздері Γк
иж арқылы беріледі
қайда ж11 = E, ж12 = F, ж22 = G және жиж -ге кері матрица болып табылады жиж. Эйлер теңдеулерін қанағаттандыратын жол а деп аталады геодезиялық. Бойынша Коши-Шварц теңсіздігі энергияны минимизациялайтын жол - бұл тек доға ұзындығымен анықталған геодезиялық параметр; және кез-келген геодезиялық үшін параметр т ұзындыққа пропорционалды.[60]
Геодезиялық қисықтық
The геодезиялық қисықтық кж қисық нүктесінде c(т), доға ұзындығымен параметрленген, бағытталған бағдарланған бетінде[61]
қайда n(т) бірліктің жанама векторын айналдыру арқылы салынған, бетіндегі қисыққа қалыпты «негізгі» бірлік ċ(т) + 90 ° бұрыш арқылы.
- Нүктедегі геодезиялық қисықтық тек нүктеге жақын метрикаға байланысты ішкі инвариант болып табылады.
- Беттің жылдамдық қисығы - бұл геодезиялық, егер оның геодезиялық қисықтығы қисықтың барлық нүктелерінде жоғалып кетсе ғана.
- Бірлік жылдамдығы қисығы c(т) ендірілген бетте геодезиялық болып табылады, егер оның үдеу векторы болса c̈(т) бетіне қалыпты.
Геодезиялық қисықтық жер бетіндегі қисық сызықтың геодезиядан қаншалықты алыс екенін дәл өлшейді.
Ортогональ координаттар
Қашан F = 0 координаттар диаграммасында, мысалы, төменде қарастырылған геодезиялық полярлық координаталарда, параллель түзулердің кескіндері х- және ж- салықтар ортогоналды және қамтамасыз ету ортогоналды координаталар. Егер H = (EG)1⁄2, содан кейін Гаусс қисығы беріледі[62]
Егер қосымша болса E = 1, сондай-ақ H = G1⁄2, содан кейін бұрыш φ геодезиялық қиылыста (х(т),ж(т)) және сызық ж = тұрақты теңдеу арқылы беріледі
Туындысы φ Гаусстың классикалық туынды формуласымен берілген:[63]
Геодезиялық полярлық координаттар

Метрика бетке беріліп, базалық нүкте бекітілгеннен кейін базалық нүктені әрбір жақын орналасқан нүктелермен байланыстыратын ерекше геодезиялық болады. Негізгі нүктедегі геодезиялық бағыт және қашықтық басқа соңғы нүктені ерекше анықтайды. Деректер мен бағыттың екі биті осылайша базалық нүктеде жанама векторды анықтайды. Тангенс векторларынан соңғы нүктелерге дейінгі карта базалық нүктенің маңайын тегіс сыпырады және сол нүктеде жергілікті координаталар диаграммасын анықтай отырып, «экспоненциалды карта» деп аталады. Төңкеріліп алынған көршілестік Евклид кеңістігіндегі шарларға ұқсас қасиеттерге ие, яғни ондағы кез-келген екі нүкте бірегей геодезиямен біріктіріледі. Бұл қасиет «геодезиялық дөңес», ал координаттар «қалыпты координаттар» деп аталады. Қалыпты координаталардың нақты есебін геодезия қанағаттандыратын дифференциалдық теңдеуді қарастыру арқылы жүзеге асыруға болады. Дөңес қасиеттер салдары болып табылады Гаусс леммасы және оны жалпылау. Бұл леммада, геодезия базалық нүктеден басталатын, радиустың радиус сфераларын базалық нүктеге тік бұрыштармен қиып тастауы керек дейді. Геодезиялық полярлық координаталар экспоненциалды картаны полярлық координаталармен жанама векторлардағы базалық нүктеде біріктіру арқылы алынады. Содан кейін беттің Гаусс қисығы метрияның эвклид метрикасынан нүктесінде екінші ретті ауытқуымен беріледі. Атап айтқанда, Гаусс қисықтығы метриканың инварианты болып табылады, Гаусс атап өтті Егрегия теоремасы. Қисықтықты түсінудің ыңғайлы тәсілі, алдымен Гаусс қарастырған, кейінірек Джакоби жалпылаған кәдімгі дифференциалдық теңдеуден туындайды, бұл екі түрлі нүкте туралы қалыпты координаталардың өзгеруінен туындайды. Гаусс-Якоби теңдеуі Гаусс қисықтығын есептеудің тағы бір әдісін ұсынады. Геометриялық тұрғыдан геодезияға не болатынын тіркелген базалық нүктеден түсіндіреді, өйткені соңғы нүкте қисық сызығының кішігірім сегменті бойымен өзгеріп отырады. Якоби өрісі, а векторлық өріс геодезиялық бойымен.[64] Гаусс пен Якобиден бір ширек ғасыр өткен соң, Марстон Морз Якоби өрісін шексіз өлшемдегі энергетикалық функцияның екінші туындылары тұрғысынан концептуалды интерпретациялады Гилберт жолдар.[65]
Экспоненциалды карта
Теориясы қарапайым дифференциалдық теңдеулер егер екенін көрсетсе f(т, v) тегіс, содан кейін дифференциалдық теңдеу дв/дт = f(т,v) бастапқы шартпен v(0) = v0 үшін ерекше шешімі бар |т| жеткілікті кішкентай және шешім тегіс байланысты т және v0. Бұл жеткілікті аз екенін білдіреді жанасу векторлары v берілген сәтте б = (х0,ж0), геодезия бар cv(т) (-2,2) -мен анықталған cv(0) = (х0,ж0) және ċv(0) = v. Сонымен қатар, егер |с| ≤ 1, содан кейін csv = cv(ст). The экспоненциалды карта арқылы анықталады
- экспб(v) = cv (1)
және дискінің арасында диффеоморфизм береді ‖v‖ < δ және б; жалпы карта жіберу (б,v) дейін экспб(v) локальді диффеоморфизмді жақын маңға береді (б,б). Экспоненциалды карта береді геодезиялық қалыпты координаттар жақын б.[66]
Қалыпты координаттарды есептеу
Стандартты техника бар (мысалы, қараңыз) Бергер (2004) ) айнымалылардың қалыпты координаттарға өзгеруін есептеу үшін сен, v Тейлор сериясының ресми кеңеюі ретінде. Егер координаталар болса х, ж at (0,0) жергілікті ортогоналды, жазыңыз
- х(сен,v) = αu + L(сен,v) + λ(сен,v) + …
- ж(сен,v) = βv + М(сен,v) + μ(сен,v) + …
қайда L, М квадраттық және λ, μ текше біртекті көпмүшелер жылы сен және v. Егер сен және v бекітілген, х(т) = х(ту,теледидар) және ж(т) = ж(ту, теледидар) формальды деп санауға болады қуат сериясы Эйлер теңдеулерінің шешімдері: бұл ерекше түрде анықталады α, β, L, М, λ және μ.
Гаусс леммасы

Бұл координаттарда матрица ж(х) қанағаттандырады ж(0) = Мен және сызықтар т ↦ теледидар Эйлер теңдеулері матрицалық теңдеуді білдіреді
- ж(v)v = v,
негізгі нәтиже, әдетте деп аталады Гаусс леммасы. Геометриялық тұрғыдан бұл туралы айтады
0 арқылы геодезия 0-ге бағытталған шеңберлерді қиып алады ортогоналды.
Қабылдау полярлық координаттар (р,θ), метриканың формасы болады
- ds2 = доктор2 + G(р,θ) dθ2.
Геодезиялық координаттарда нөлге дейінгі геодезияның ұзындығын минимизациялайтындығын тексеру оңай. Риман коллекторындағы топологияны а қашықтық функциясы г.(б,q), атап айтқанда шексіз арасындағы кесек-кесек тегіс жолдардың ұзындықтары б және q. Бұл қашықтықты жергілікті координаттарда геодезия жүзеге асырады г.(0,v) = ‖v‖. Егер радиус δ аз мөлшерде алынады, Гаусс лемманың сәл қайралуы кескін екенін көрсетеді U дискінің ‖v‖ < δ экспоненциалды картаның астында орналасқан геодезиялық дөңес, яғни кез-келген екі нүкте U толығымен ішінде орналасқан бірегей геодезиялық қосылады U.[67][68]
Егрегия теоремасы
Гаусстың Егрегия теоремасы, «ғажайып теорема», беттің Гаусс қисықтығын тек метрика бойынша есептеуге болатындығын және осылайша беттің ішкі инвариантты екенін, кез-келгенге тәуелді емес екенін көрсетеді изометриялық енгізу жылы E3 және координаталық түрлендірулер кезінде өзгеріссіз. Атап айтқанда, беттердің изометриялары Гаусстың қисаюын сақтайды.[69]
Бұл теореманы метриканың күштік қатарының кеңеюі арқылы көрсетуге болады, ds, қалыпты координаттарда берілген (сен, v) сияқты
- ds2 = ду2 + дв2 − Қ(сен дв – v du)2/12 + ….
Гаусс-Якоби теңдеуі
Кезінде қалыпты координаттардан координатаның өзгеруін алу б жақын орналасқан нүктеде қалыпты координаталарға дейін q, өнімді береді Штурм-Лиувилл теңдеуі қанағаттандырады H(р,θ) = G(р,θ)1⁄2, Гаусс және кейінірек жалпыланған арқылы Якоби,
Hrr = –KH
The Якобиан осы координатаның өзгеруі q тең Hр. Бұл Гаусс қисаюының ішкі табиғатын орнатудың тағы бір әдісін береді. Себебі H(р,θ) ішіндегі сызық элементінің ұзындығы ретінде түсіндіруге болады θ бағыты бойынша Гаусс-Якоби теңдеуі Гаусс қисықтығы геодезияның геометриялық бетке олардың нүктеден алшақтау кезінде таралуын өлшейтіндігін көрсетеді.[70]
Laplace - Beltrami операторы
Жергілікті метрика бар бетінде
және Laplace - Beltrami операторы
қайда H2 = EG − F2, нүктедегі Гаусстың қисаюы формула бойынша берілген[71]
қайда р нүктеден геодезиялық қашықтықты білдіреді.
Жылы изотермиялық координаттар, алдымен Гаусс қарастырған, метрика арнайы формада болуы керек
Бұл жағдайда Laplace-Beltrami операторы арқылы беріледі
және φ қанағаттандырады Лиувилл теңдеуі[72]
Изотермиялық координаттар жердің кез-келген нүктесінің маңында бар екендігі белгілі, дегенмен бүгінгі күнге дейін барлық дәлелдер маңызды емес нәтижелерге негізделген дербес дифференциалдық теңдеулер.[73] Минималды беттерге қарапайым дәлелдемелер бар.[74]
Гаусс-Бонет теоремасы

Үстінде сфера немесе а гиперболоидты, геодезиялық үшбұрыштың ауданы, яғни барлық қабырғалары геодезия болатын үшбұрыш ішкі бұрыштардың қосындысының айырымына пропорционалды және π. Пропорционалдылықтың тұрақтысы - бұл тек беттер үшін тұрақты Гаусс қисығы. Торус үшін айырмашылық нөлге тең, оның Гаусстың қисаюы нөлге тең екендігін көрсетеді. Бұл сфералық, гиперболалық және орта тригонометрияның стандартты нәтижелері (төменде қараңыз). Гаусс бұл нәтижелерді геодезиялық үшбұрыштың ішкі жағындағы Гаусс қисаюының интегралының осы бұрыш айырымына немесе артықтығына тең болатындығын көрсетіп, ерікті бетке жалпылаған. Оның формуласы Гаусс қисықтығын геодезиялық үшбұрыштар үшін бұрыштың артықтығынан асатын ауданның шекарасы нүктеге дейін есептелетіндігін көрсетті. Кез-келген тұйық бетті геодезиялық үшбұрышқа дейін ыдыратуға болатындықтан, формуланы бүкіл бетке қисықтық интегралын есептеу үшін де қолдануға болады. Қазіргі уақытта деп аталатын ерекше жағдай ретінде Гаусс-Бонет теоремасы, Гаусс бұл интегралдың әрдайым бүтін саннан 2π есе үлкен болатындығын дәлелдеді, бұл беттің топологиялық инварианты деп аталады Эйлерге тән. Бұл инвариантты ыдыратудағы үшбұрыштардың төбелері, шеттері мен беттерінің саны бойынша комбинативті түрде есептеу оңай, оны а деп те атайды. триангуляция. Талдау мен топологияның өзара әрекеттесуі геометриядағы көптеген кейінгі нәтижелердің ізашары болды Atiyah-Singer индекс теоремасы. Қисықтықтың ерекше қасиеттері беткі топологияға шектеулер қояды.
Геодезиялық үшбұрыштар
Гаусс дәлелдеді, егер Δ - бұрыштары бар бетіндегі геодезиялық үшбұрыш α, β және γ шыңдарда A, B және C, содан кейін
Іс жүзінде геодезиялық полярлық координаттарды шығу тегі бойынша қабылдау A және AB, Айнымалы 0 және полярлық бұрыштардағы радиустар α:
Мұндағы екінші теңдік Гаусс-Джакоби теңдеуінен, ал төртіншісі ортогоналды координаталардағы Гаусстың туынды формуласынан шығады. (р,θ).
Гаусстың формуласы нүктедегі қисықтықты шегі ретінде есептеуге болатындығын көрсетеді артық бұрыш α + β + γ - π аяқталды аудан нүктеге жақын орналасқан геодезиялық үшбұрыштар үшін. Сапалы түрде бет ерікті түрде кішігірім геодезиялық үшбұрыштар үшін бұрыштың артық болу белгісіне сәйкес оң немесе теріс қисық болады.[75]
Гаусс-Бонет теоремасы

Әрбір ықшам бағытталған 2-коллекторлы болғандықтан М бола алады үшбұрышты кішігірім геодезиялық үшбұрыштар арқылы шығады
қайда χ(М) дегенді білдіреді Эйлерге тән бетінің
Егер бар болса F жүздер, E шеттері және V шыңдар, содан кейін 3F = 2E ал сол жағы тең 2πV - πF = 2π (V – E + F) = 2πχ(М).
Бұл мерекеленген Гаусс-Бонет теоремасы: бұл Гаусс қисығының интегралының коллектордың топологиялық инварианты, яғни Эйлер сипаттамасы екендігін көрсетеді. Бұл теореманы әр түрлі түсіндіруге болады; мүмкін, ең ауқымдыларының бірі ан үшін индекс теоремасы болды эллиптикалық дифференциалдық оператор қосулы М, қарапайым жағдайлардың бірі Atiyah-Singer индекс теоремасы. Гаусс-Бонн теоремасын пайдаланып дәлелдеуге болатын тағы бір ұқсас нәтиже - бұл Пуанкаре-Хопф индексі теоремасы векторлық өрістер үшін М тек нүктелердің шектеулі санында жоғалады: осы нүктелердегі индекстердің қосындысы Эйлер сипаттамасына тең, мұндағы индекс нүктенің анықтамасы келесідей: әр оқшауланған нөлдің айналасындағы кіші шеңберде векторлық өріс бірлік шеңбер шеңберінде картаны анықтайды; индекс тек орам нөмірі осы картаның.)[75][76][77]
Қисықтық және ендіру
Егер бетінің қисықтығы Гаусс болса М барлық жерде позитивті, сондықтан Эйлердің сипаттамасы оң болады М геомоморфты болып табылады (демек, диффеоморфты) S2. Егер қосымша беті изометриялық ендірілген болса E3, Гаусс картасы айқын диффеоморфизмді ұсынады. Қалай Хадамард байқалады, бұл жағдайда беті болып табылады дөңес; бұл дөңестіктің критерийін жазықтық қисықтарының дөңестігінің белгілі екінші туынды критерийін 2-өлшемді жалпылау ретінде қарастыруға болады. Гильберт әрбір изометриялық ендірілген тұйық бетінің оң қисықтық нүктесі болуы керек екенін дәлелдеді. Осылайша, оң емес қисықтықтың жабық римандық 2-коллекторы ешқашан изометриялық түрде ене алмайды E3; дегенмен Адриано Гарсия қолданғанын көрсетті Бельтрами теңдеуі үшін квазиконформальды кескіндер, бұл әрқашан кейбіреулер үшін мүмкін сәйкес эквивалент метрикалық.[78]
Тұрақты қисықтықтың беттері
The жай қосылған 0, +1 және –1 тұрақты қисықтық беттері - эвклид жазықтығы, бірлік сферасы E3, және гиперболалық жазықтық. Бұлардың әрқайсысы үш өлшемді өтпелі сипатқа ие Өтірік тобы бағдарларды сақтау изометрия G, олардың көмегімен геометрияны зерттеуге болады. Екі ықшам емес беттің әрқайсысын квотамен сәйкестендіруге болады G / Қ қайда Қ Бұл максималды ықшам топша туралы G. Мұнда Қ изоморфты болып табылады СО (2). Кез-келген басқа жабық Riemannian 2-коллекторы М егер қажет болса, метроны тұрақты коэффициент бойынша масштабтағаннан кейін, тұрақты Гаусс қисықтығы осы үш беттің біріне тең болады әмбебап қамту кеңістігі. Бағдарланған жағдайда іргелі топ Γ туралы М арқылы анықтауға болады бұралмалы емес бірыңғай кіші топ туралы G және М содан кейін космостық кеңістік Γ G / Қ. Сфера мен Евклид жазықтығы жағдайында тек мысал ретінде сфераның өзі мен tori квотенті ретінде алынған болуы мүмкін. R2 дискретті дәреже бойынша 2 кіші топтар бойынша. Жабық беттері үшін түр ж ≥ 2, кеңістік ретінде алынған Риман беттерінің Γ барлық осындай кіші топтарда өзгереді, нақты өлшемдері бар 6ж − 6.[79] Пуанкаредікі теңдестіру теоремасы, кез-келген бағдарланған тұйықталған 2-коллектор сәйкес эквивалент тұрақты қисықтық бетіне 0, +1 немесе –1. Басқаша айтқанда, метриканы масштабтаудың оң коэффициентіне көбейту арқылы Гаусс қисықтығын дәл осы мәндердің біреуін алуға болады (белгісі Эйлерге тән туралы М).[80]
Евклидтік геометрия

Евклид жазықтығы жағдайында симметрия тобы болып табылады Евклидтік қозғалыс тобы, жартылай бағыт өнім айналу тобы бойынша аудармалардың екі өлшемді тобының.[81] Геодезия - бұл түзу сызықтар, ал геометрия -ның қарапайым формулаларында кодталған тригонометрия сияқты косинус ережесі қабырғалары бар үшбұрыш үшін а, б, c және бұрыштар α, β, γ:
Тори тегісін квотаны алу арқылы алуға болады R2 а тор, яғни 2-дәрежелі абельдік кіші топ. Бұл жабық беттерде изометриялық ендірулер жоқ E3. Олар изометриялық енгізулерді мойындайды E4; ең қарапайым жағдайда, бұл торус екі шеңбердің көбейтіндісі болып табылады және әрбір шеңберді изометриялық түрде енгізуге болады E2.[82]
Сфералық геометрия

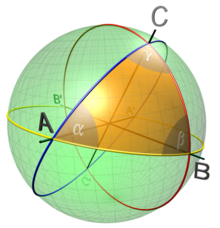
Бірлік сферасының изометрия тобы S2 жылы E3 ортогональды топ болып табылады O (3), бірге айналу тобы Ж (3) бағдарды сақтайтын изометриялардың кіші тобы ретінде. Бұл тікелей өнімі Ж (3) бірге антиподальды карта, жіберіліп жатыр х дейін –х.[83] Топ Ж (3) өтпелі түрде әрекет етеді S2. The тұрақтандырғыш топшасы бірлік векторының (0,0,1) көмегімен анықтауға болады СО (2), сондай-ақ S2 = SO (3) / SO (2).
Шардағы екі нүктенің арасындағы геодезия - болып табылады үлкен шеңбер осы соңғы нүктелері бар доғалар. Егер нүктелер антиподальды болмаса, нүктелер арасында бірегей ең қысқа геодезия бар. Геодезияны теориялық тұрғыдан да сипаттауға болады: әр геодезия - Солтүстік полюс (0,0,1) арқылы экватордағы антиподальды нүктелер арқылы ось бойынша айналудың кіші тобы орбитасы болып табылады.
A сфералық үшбұрыш - сферадағы геодезиялық үшбұрыш. Ол нүктелермен анықталады A, B, C жағы бар сферада Б.з.д., Калифорния, AB ұзындықтан үлкен шеңбер доғаларынан түзілген π. Егер жақтардың ұзындықтары а, б, c және жақтар арасындағы бұрыштар α, β, γ, содан кейін сфералық косинус заңы дейді
Үшбұрыштың ауданы келесі арқылы беріледі
- Ауданы = α + β + γ - π.
Қолдану стереографиялық проекция солтүстік полюстен сфераны кеңейтілген жазықтық C ∪ {∞}. Нақты карта келтірілген
Осы сәйкестік бойынша S2 сәйкес келеді Мобиустың өзгеруі жылы СУ (2), қол қою үшін бірегей.[84] Координаттарға қатысты (сен, v) күрделі жазықтықта сфералық метрика айналады[85]
Бірлік сферасы +1 тұрақты қисықтықпен бірегей тұйық бағдарланған бет болып табылады. Көрсеткіш SO (3) / O (2) көмегімен анықтауға болады нақты проективті жазықтық. Ол бағдарланбайды және оның мәні ретінде сипатталуы мүмкін S2 антиподальды карта бойынша (көбейту by1). Нақты проекциялық жазықтықта іргелі топ бар, ал сфера жай ғана байланысты З2. The соңғы топтары Ж (3), -дің ақырғы топшаларына сәйкес келеді O (2) және симметрия топтары платондық қатты заттар, еркін әрекет етпеңіз S2, сондықтан сәйкес квотенттер тек 2-коллекторлы емес орбифолдтар.
Гиперболалық геометрия

Евклидтік емес геометрия[86] ХІХ ғасырдың басында кең есептеулер жасаған Гаусстың хаттарында алғаш рет талқыланды, ол жеке таралыммен болса да, баспаға шығармауға шешім қабылдады. 1830 жылы Лобачевский және өз бетінше 1832 ж Боляй, бір Гаусстың корреспонденттерінің ұлы осы жаңа геометрияның синтетикалық нұсқаларын жариялады, ол үшін олар қатты сынға алынды. Алайда 1868 жылға дейін ғана Бельтрами, кейіннен Клейн 1871 жылы және Пуанкаре 1882 жылы Клейн атаған нақты аналитикалық модельдерді берді гиперболалық геометрия. Екі өлшемді гиперболалық геометрияның төрт моделі пайда болды:
- The Beltrami-Klein моделі;
- The Пуанкаре дискісі;
- The Пуанкаре жоғарғы жарты жазықтық;
- The гиперболоидтық модель туралы Вильгельмді өлтіру 3-өлшемді Минковский кеңістігі.
Дискіге негізделген бірінші модельдің артықшылығы геодезия іс жүзінде сызықтық сегменттер болып табылады (яғни эвклидтік сызықтардың ашық блок дискісімен қиылысуы). Соңғы модельдің артықшылығы бар, ол үш өлшемді эвклид кеңістігіндегі бірлік сфераға толығымен параллель болатын құрылысты береді. Күрделі анализде және геометрияда қолданғандықтан, Пуанкаренің модельдері кеңінен қолданылады: олар диск пен жоғарғы жарты жазықтық арасындағы Мобиус түрлендірулерінің арқасында ауыстырылады.
Келіңіздер
болуы Пуанкаре дискісі күрделі жазықтықта Пуанкаре метрикасы
Полярлық координаттарда (р, θ) метрика арқылы беріледі
Қисықтың ұзындығы γ:[а,б] → Д. формула бойынша берілген
Топ G = СУ (1,1) берілген
арқылы өтпелі түрде әрекет етеді Мобиус түрлендірулері қосулы Д. және тұрақтандырғыш топшасы 0 - айналу тобы
Келесі топ SU (1,1) / ±Мен бағдар сақтайтын изометриялардың тобы болып табылады Д.. Кез-келген екі ұпай з, w жылы Д. шеңбер немесе түзу сызық арқылы өтетін ерекше геодезиямен қосылады з және w және шекаралық шеңберге ортогоналды. Арасындағы қашықтық з және w арқылы беріледі
Соның ішінде г.(0,р) = 2 тан−1 р және c(т) = 1/2танх т - нақты ось бойымен 0 арқылы геодезиялық, ұзындығы бойынша параметрленген.
Бұл метрикамен анықталған топология метрикалық кеңістік ретінде болса да, әдеттегі евклидтік топологияға баламалы (Д.,г.) аяқталды.
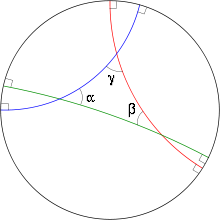
A гиперболалық үшбұрыш бұл көрсеткіш үшін геодезиялық үшбұрыш: кез келген үш нүкте Д. гиперболалық үшбұрыштың төбелері. Егер жақтардың ұзындығы болса а, б, c сәйкес бұрыштармен α, β, γ, содан кейін косинустың гиперболалық ережесі бұл туралы айтады
Гиперболалық үшбұрыштың ауданы -мен берілген[87]
- Ауданы = π - α – β – γ.
Бірлік дискісі және жоғарғы жарты жазықтық
Мобиус түрлендірулерімен сәйкесінше эквивалентті
Осы сәйкестік бойынша SL (2, R) Мобиус түрлендіруі бойынша H сәйкес келеді СУ (1,1) қосулы Д.. Көрсеткіш қосулы H болады
Мобиус түрлендірулерінде сызықтар немесе шеңберлер сақталғандықтан, геодезия қайтадан нақты оське ортогональ сызықтармен немесе шеңберлермен сипатталады.
Пуанкаре метрикасы бар бірлік диск - simply1 тұрақты қисықтыққа ие, бір-біріне қарапайым бағытталған 2 өлшемді Риман коллекторы. Кез-келген бағдарланған тұйық бет М осы қасиеті бар Д. оның әмбебап жабу кеңістігі ретінде. Оның іргелі топ бұралусыз ықшам топшамен анықтауға болады Γ туралы СУ (1,1), осылай
Бұл жағдайда Γ Бұл түпкілікті ұсынылған топ. Генераторлар мен қатынастар геодезиялық дөңеспен кодталған іргелі геодезиялық көпбұрыш жылы Д. (немесе Hжабық геодезияға геометриялық сәйкес келеді М.
Мысалдар.
- The Болза беті 2 тұқымдас;
- The Клейн квартикасы 3 тұқым;
- The Macbeath беті 7 тұқымдас;
- The Бірінші Хурвиц үштік 14-түр.
Бірыңғайлау
Бағдарланған тұйық бет берілген М қисаюымен Қ, метрика қосулы М оны коэффициент бойынша масштабтау арқылы конформды түрде өзгертуге болады e2сен. Жаңа Гаусс қисығы K ′ содан кейін беріледі
қайда Δ бастапқы метрика үшін лаплациан болып табылады. Осылайша, берілген беттің тұрақты қисықтықпен метрикаға конформды түрде эквивалентті екендігін көрсету K ′ келесі нұсқасын шешу жеткілікті Лиувилл теңдеуі:
Қашан М Эйлерге 0 тән, сондықтан а-ға диффеоморфты торус, K ′ = 0, сондықтан бұл шешуге тең келеді
Стандартты эллиптикалық теория бойынша бұл мүмкін, өйткені Қ аяқталды М Гаусс-Бонн теоремасы бойынша нөлге тең.[88]
Қашан М Эйлердің жағымсыз сипаттамалары бар, K ′ = −1, сондықтан шешілетін теңдеу:
Бойынша экспоненциалды картаның үздіксіздігін пайдалану Соболев кеңістігі байланысты Нил Трудингер, бұл сызықтық емес теңдеуді әрқашан шешуге болады.[89]
Соңында, 2-сфера жағдайында, K ′ = 1 және теңдеу:
Осы сияқты сызықтық емес теңдеу тікелей талданған жоқ, дегенмен классикалық нәтижелер сияқты Риман-Рох теоремасы оның әрдайым шешімі бар екенін білдіреді.[90] Әдісі Ricci ағыны, әзірлеген Ричард С. Хэмилтон, сызықтық емеске негізделген тағы бір дәлелдеме береді дербес дифференциалдық теңдеулер тіршілік етуді дәлелдеу.[91] Шын мәнінде Ricci ағыны конформды көрсеткіштер бойынша жүреді S2 функциялар бойынша анықталады сен(х, т) арқылы
Соңғы уақыттан кейін Чоу мұны көрсетті K ′ позитивті болады; Гамильтонның алдыңғы нәтижелері мұны көрсету үшін қолданыла алады K ′ +1 мәніне жақындайды.[92] Осы нәтижелерге дейін Ricci ағыны, Osgood, Phillips & Sarnak (1988) Риман метрикасы бойынша ағынға негізделген біркелкі етуге альтернативті және техникалық тұрғыдан қарапайым тәсіл ұсынды ж арқылы анықталады log det Δж.
1988 жылы ашылған тек эллиптикалық операторларды қолдана отырып қарапайым дәлелдеуді табуға болады Дин (2001). Келіңіздер G болуы Жасыл функция қосулы S2 қанағаттанарлық ΔG = 1 + 4πδP, қайда δP - бұл белгіленген нүктедегі нүктелік өлшем P туралы S2. Теңдеу Δv = 2Қ – 2, тегіс шешімі бар v, өйткені оң жақта Гаусс-Бонн теоремасы бойынша 0 интегралды болады. Осылайша φ = 2G + v қанағаттандырады Δφ = 2Қ алыс P. Бұдан шығатыны ж1 = eφж - толықтауышындағы 0 тұрақты қисықтықтың толық метрикасы P, ол жазықтыққа изометриялық болып табылады. Композиторлық стереографиялық проекция, тегіс функция бар екендігі шығады сен осындай e2сенж қосымшасында Гаусс қисығы +1 бар P. Функция сен автоматты түрде толығымен тегіс функцияға дейін созылады S2.[b]
Риман байланысы және параллель тасымалдау

Беттердің дифференциалды геометриясына Гаусстың классикалық тәсілі стандартты қарапайым тәсіл болды[93] ұғымдары пайда болғанға дейінгі Риманн коллекторы бастамашы Бернхард Риман ХІХ ғасырдың ортасында және байланыс әзірлеген Туллио Леви-Сивита, Эли Картан және Герман Вейл ХХ ғасырдың басында. Байланыс ұғымы, ковариант туынды және параллель тасымалдау қисықтықты түсінудің неғұрлым тұжырымдамалық және біркелкі әдісін берді, бұл тек жоғары өлшемді коллекторларға жалпылауға мүмкіндік беріп қана қоймай, сонымен қатар жаңа геометриялық инварианттарды анықтайтын маңызды құрал болды сипаттағы сыныптар.[94] Ковариантты туындылар мен байланыстарды қолдану тәсілі қазіргі кезде анағұрлым жетілдірілген оқулықтарда қолданылады.[95]
Ковариант туындысы
Беттегі байланыстарды әр түрлі эквивалентті, бірақ бірдей маңызды көзқарастардан анықтауға болады. The Риман байланысы немесе Levi-Civita байланысы.[96] көтеру тұрғысынан оңай түсініледі векторлық өрістер, бірінші рет қарастырылған дифференциалдық операторлар коллектордағы функцияларға, дифференциалды операторларға әсер ету тангенс байламы немесе жақтау байламы. Кірістірілген бет жағдайында векторлық өрістердегі операторға лифт деп аталады ковариант туынды, ортогоналды проекция тұрғысынан өте қарапайым сипатталған. Шынында да, ендірілген бетіндегі векторлық өріс R3 функциясын жер бетінен қарастыруға болады R3. Басқа векторлық өріс компоненттің дифференциалдық операторы ретінде жұмыс істейді. Алынған векторлық өріс бетке жанама болмайды, бірақ оны түзетуге болады, егер оның бетінің әр нүктесінде жанама кеңістікке ортогональ проекциясы жасалса. Қалай Риччи және Леви-Сивита ХХ ғасырдың басында жүзеге асырылған бұл процесс тек метрикаға тәуелді және жергілікті жерде Кристоффель рәміздері арқылы көрсетілуі мүмкін.

Параллельді тасымалдау
Параллельді тасымалдау жанасу векторларының бетіндегі қисық бойымен болуы тақырыптың келесі алға жылжуы болды Леви-Сивита.[75] Бұл ковариант туындысының бұрынғы түсінігімен байланысты, өйткені ол монодромия туралы қарапайым дифференциалдық теңдеу қисықтың жылдамдық векторына қатысты ковариантты туындымен анықталған қисықта. Геодезия бойынша параллельді тасымалдауды, беттің «түзу сызықтарын» да тікелей сипаттауға болады. Тангенс жазықтығындағы вектор геодезия бойымен тұрақты ұзындықтағы және геодезияның жылдамдық векторымен тұрақты бұрыш жасайтын бірегей векторлық өріс ретінде тасымалданады. Жалпы қисық үшін бұл процесті геодезиялық қисықтықтан өзгерту керек, ол қисықтың геодезиялық болудан қаншалықты алшақтайтындығын өлшейді.[67]
Векторлық өріс v(т) жылдамдық бірлігінің қисығы бойымен c(т), геодезиялық қисықтықпен кж(т), егер қисық бойымен параллель болады дейді
- оның тұрақты ұзындығы бар
- бұрыш θ(т) ол жылдамдық векторымен жасайды ċ(т) қанағаттандырады
Бұл геодезиялық немесе кесек геодезиялық қисық бойымен параллель тасымалдау ережесін қалпына келтіреді, өйткені бұл жағдайда кж = 0, сондықтан бұрыш θ(т) кез келген геодезиялық сегментте тұрақты болып қалуы керек. Параллель тасымалдаудың болуы келесіден туындайды θ(т) ретінде есептелуі мүмкін ажырамас геодезиялық қисықтық. Бұл үнемі байланысты болғандықтан L2 нормасы кж, ерікті қисық үшін параллель тасымалдауды жақындастырылған кесек геодезиялық қисықтардағы параллель тасымалдаудың шегі ретінде алуға болады деген қорытынды шығады.[97]
Осылай байланыстыруды манжеттердегі тангенс немесе ортонормальды рамалық шоғырдағы жолдарға көтеру жолдары арқылы сипаттауға болады, осылайша классикалық теорияны «жылжымалы жақтау », француз авторлары ұнатады.[98] Ілмектерді бір нүктеге қатысты көтеру нәтижесінде пайда болады голономия тобы сол кезде. Нүктедегі Гаусстың қисаюын нүктеде кішігірім ілмектер айналасында параллель тасымалдаудан қалпына келтіруге болады. Эквивалентті қисықтықты тікелей шексіз деңгейде есептеуге болады Қыстырмалар көтерілген векторлық өрістер.

Байланыс 1-форма
Картан мен Вейлдің 1-формадағы байланысын қолдана отырып жақындауы жақтау байламы туралы М, Риман байланысын түсінудің үшінші әдісін береді. Олар параллель тасымалдау бетіндегі жолды рамка байламындағы жолға көтеруге болатынын, оның жанасу векторлары раманың байламының үш өлшемді тангенс кеңістігіндегі бір кодмерліктің арнайы кіші кеңістігінде жататындығын байқаған. Осы кіші кеңістікке проекция ортонормальді рамалық дестедегі дифференциалдық 1-формамен анықталады, байланыс формасы. Бұл беттің қисықтық қасиеттерін кодтауға мүмкіндік берді дифференциалды формалар рамалық бумада және олардың қатысуымен формулалар сыртқы туындылар.
Бұл тәсіл ендірілген беті үшін өте қарапайым. Нәтижесі арқасында Кобаяши (1956), Евклид кеңістігіне енген беттегі байланыс 1-форма E3 бұл байланыс формасының Гаусс картасы астындағы кері байланыс S2.[99] Идентификациясын қолдану S2 бірге біртекті кеңістік SO (3) / SO (2), 1-форма байланысы -ның құрамдас бөлігі ғана Маурер-Картан 1-формасы қосулы Ж (3).[100]
Беттердің ғаламдық дифференциалды геометриясы
Қисықтық сипаттамасы тек беттің жергілікті геометриясын қамтығанымен, сияқты жаһандық аспектілер бар Гаусс-Бонет теоремасы, теңдестіру теоремасы, фон Мангольдт-Хадамар теоремасы және енімділік теоремасы. Беттердің ғаламдық геометриясының басқа маңызды аспектілері бар.[101] Оларға мыналар жатады:
- Инъекция радиусы, ең үлкені ретінде анықталды р арақашықтықта екі нүкте кем болатындай етіп р бірегей геодезиялық қосылады. Вильгельм Клингенберг 1959 жылы тұйық беттің инъекциялық радиусының төменде минимуммен шектелетіндігін дәлелдеді δ = π/√суп Қ және оның ең кіші жабық геодезиялық ұзындығы. Бұл 1855 жылы оң Гаусс қисаюының тұйық бетінің диаметрі әрдайым жоғарыда шектелгенін көрсеткен Бонет теоремасын жақсартты. δ; басқаша айтқанда, екі нүкте арасындағы метрикалық арақашықтықты жүзеге асыратын геодезиялық ұзындықтан үлкен бола алмайды δ.
- Қаттылық. 1927 жылы Кон-Воссен екеуін дәлелдеді овалоидтар - оң гаусс қисықтығы бар жабық беттер - изометриялық болып табылады, міндетті түрде изометриямен сәйкес келеді E3. Сонымен қатар, оң Гаусс қисықтығы мен орташа орташа қисықтығы бар тұйық ендірілген бет міндетті түрде сфера болып табылады; сол сияқты тұрақты Гаусс қисығының жабық ендірілген беті сфера болуы керек (Либманн 1899). Хайнц Хопф 1950 жылы орташа қисықтық пен тектес 0, яғни сфераға гомеоморфты болатын тұйық ендірілген бет міндетті түрде сфера екенін көрсетті; бес жылдан кейін Александров топологиялық болжамды алып тастады. 1980 жылдары Венте салынды батырылған Евклидтік 3 кеңістігіндегі орташа орташа қисықтықтың торы.
- Каратеодорлық болжам: Бұл болжам бойынша тұйық дөңес үш есе дифференциалданатын бет кем дегенде екеуін қабылдайды кіндік нүктелері. Бұл болжам бойынша алғашқы жұмыс 1924 жылы болды Ганс Гамбургер, ол келесі күшті талаптан туындайтынын атап өтті: оқшауланған кіндіктің негізгі қисықтық жапырағының жарты бүтін индексі ең көбі.
- Гаусстың нөлдік қисықтығы: толық беті E3 нөлдік гаусс қисықтығы цилиндр немесе жазықтық болуы керек.
- Гильберт теоремасы (1901): тұрақты теріс қисықтықпен толық бет болуы мүмкін емес батырылған изометриялық E3.

- The Уиллмор болжам. Бұл болжамға сәйкес, торустың орташа қисықтық квадратының интегралы E3 төменде шектелуі керек 2π2. Интеграл Moebius инвариантты екені белгілі. Ол 2012 жылы шешілді Фернандо Кода Маркес және Андре Невес.[102]
- Изопериметриялық теңсіздіктер. 1939 жылы Шмидт Евклид жазықтығындағы қисықтар үшін классикалық изопериметриялық теңсіздік сферада немесе гиперболалық жазықтықта да жарамды екенін дәлелдеді: дәлірек айтқанда, ол тіркелген ауданның доменін шектейтін барлық тұйық қисықтардың ішінде периметр қисық кезіндегі минимумға дейін азаяды. метриканың шеңбері болып табылады. Бір өлшемнен жоғары, барлық жабық беттердің ішінде E3 көлем бірлігінің шектелген аймағының шекарасы ретінде туындайтын болса, евклидтік шар үшін бетінің ауданы азайтылады.
- Беттердегі қисықтардың систолалық теңсіздіктері. Тұйық бетті ескере отырып, оның систола бетіндегі кез-келген бітелмейтін тұйық қисықтың ең кіші ұзындығы ретінде анықталады. 1949 жылы Левнер дәлелденген а торус теңсіздігі тордағы метрикалар үшін, яғни оның систоласының квадратындағы тордың ауданы төменде шектелген √3/2, жазықтықтағы (тұрақты қисықтық) жағдайдағы теңдікпен. Осыған ұқсас нәтиже Нақты проективті жазықтықтағы Пудың теңсіздігі 1952 жылдан бастап, төменгі шекарасымен 2/π тұрақты қисықтық жағдайында да қол жеткізілді. Үшін Klein бөтелкесі, Блаттер мен Бавард кейінірек төменгі шегін алды √8/π. Жыныстың жабық беті үшін ж, Хебда мен Бураго қатынас төменде шектелгенін көрсетті 1/2. Үш жылдан кейін Михаил Громов тұрақты уақыттармен берілген төменгі шегін тапты ж1⁄2, бірақ бұл оңтайлы емес. Асимптотикалық өткір жоғарғы және төменгі шектер тұрақты уақытпен берілген ж/(журнал ж)2 Громов пен Бусер-Сарнакқа байланысты және оларды табуға болады Катц (2007). Сонымен қатар сферада ең кіші болатын сфераны өлшейтін нұсқа да бар жабық геодезиялық. Громов төменгі шекараны болжады 1/2√3 1980 жылы: ең жақсы нәтиже - төменгі шекара 1/8 Регина Ротман 2006 жылы алған.[103]
Оқу нұсқаулығы
Гаусстан бастап қазіргі заманға дейінгі тарихи дамуды бейнелейтін тақырыпты ең ауқымды кіріспе сауалнамалардың бірі болып табылады. Бергер (2004). Классикалық теорияның есептері келтірілген Эйзенхарт (2004), Крейциг (1991) және Струик (1988); бакалавриаттың заманауи оқулықтары неғұрлым заманауи Грей, Аббена және Саламон (2006), Прессли (2001) және Уилсон (2008) қол жетімді болуы мүмкін. Классикалық теорияның қол жетімді есебін табуға болады Гилберт және Кон-Воссен (1952). Аспирантурасын қолдана отырып, неғұрлым күрделі емдеу Жер бетіндегі римандық байланыс табуға болады Әнші және Торп (1967), до Кармо (2016) және О'Нил (2006).
Сондай-ақ қараңыз
Ескертулер
- ^ Соңғы бірнеше мәтіндерде оң жақтағы симметриялы белгісіз форма екінші іргелі форма деп аталатынын ескеріңіз; дегенмен, ол жалпы классикалық анықталған екінші іргелі формаға сәйкес келмейді.
- ^ Бұдан кейін теоремасы қатысқан аргумент шығады Sacks & Uhlenbeck (1981) -ның алынбалы ерекшеліктері туралы гармоникалық карталар ақырғы энергия.
- ^ а б Гаусс 1902.
- ^ Струк 1987 ж, 50-53 беттер
- ^ Құдықтар 2017, 17-30 бет
- ^ Эйлер 1760
- ^ Эйлер 1771
- ^ Крейсиг 1991 ж
- ^ Струк 1988 ж
- ^ Warner 1983 ж
- ^ Хитчин 2013, б. 45
- ^ Кармо 2016, 54-56 беттер
- ^ Уилсон 2008, б. 115
- ^ Прессли, 68-77 б
- ^ Кармо 2016, 55 бет
- ^ Кармо 2016, 60-65 б
- ^ O'Neill 2006, б. 113
- ^ Ли «Тегіс манифольдтерге кіріспе»
- ^ Кармо 2016, 72-бет
- ^ Струк 1988 ж
- ^ Крейциг 1991 ж
- ^ Singer & Thorpe 1966 ж, б. 100-114
- ^ Singer & Thorpe 1966 ж, б. 133-134
- ^ Кармо 2016 жасаңыз, 155-157 беттер
- ^ Do Carmo, page 235
- ^ Do Carmo, page 238
- ^ Do Carmo, pages 237-238
- ^ Struik 1961, б. 112
- ^ Darboux, Vol. III, page 246
- ^ Бергер. A panoramic view of Riemannian geometry.
- ^ O'Neill 2006, б. 257
- ^ do Carmo 2016, pp. 309–314
- ^ Hitchin 2013, б. 57
- ^ do Carmo 2016, б. 221-222
- ^ O'Neill 2006, pp. 281-289
- ^ Hitchin 2013, 57-58 б
- ^ do Carmo 2016, б. 223
- ^ do Carmo 2016, 222-223 беттер
- ^ do Carmo 2016, pp. 224-225
- ^ Do Carmo, page 183
- ^ Do Carmo, page 242
- ^ Hitchin 2013
- ^ Struik 1961
- ^ O'Neill 2006
- ^ Do Carmo, page 242
- ^ Spivak, "A comprehensive introduction to differential geometry, vol. III." Page 157.
- ^ Spivak, pages 161-166
- ^ Spivak, page 168
- ^ Eisenhart 2004, 228-229 беттер
- ^ Eisenhart 2004, pp. 241–250; do Carmo 2016, 188–197 бб.
- ^ do Carmo 2016, б. 194.
- ^ Eisenhart 2004, 61–65 б.
- ^ Eisenhart 2004
- ^ Eisenhart 2004, pp. 250–269; do Carmo 2016, pp. 197–213.
- ^ Douglas' solution is described in Courant (1950).
- ^ Eisenhart 2004, pp. 270–291; О'Нил, pp. 249–251; Хилберт және Кон-Воссен 1952 ж.
- ^ О'Нил, pp. 249–251; Кармо жаса, pp. 168–170; Gray, Abbena & Salamon 2006.
- ^ Stillwell 1996, 1-5 бет.
- ^ Уилсон 2008.
- ^ O'Neill 2006, pp. 195–216; do Carmo 2016, pp. 134–153; Singer & Thorpe 1967, pp. 216–224.
- ^ Gray, Abbena & Salamon 2006, б. 386.
- ^ Бергер 2004; Уилсон 2008; Milnor 1963.
- ^ Eisenhart 2002, б. 131; Бергер 2004, б. 39; do Carmo 2016, б. 248; O'Neill 2006, б. 237
- ^ Eisenhart 2004; Taylor 1996a, pp. 472-473, Appendix C.
- ^ Eisenhart 2004, section 88; Бергер 2004.
- ^ do Carmo 2016, б. 357
- ^ Milnor 1963
- ^ Уилсон 2008
- ^ а б Бергер 2004
- ^ do Carmo 2016, 303–305 бб
- ^ Бергер 2004, pp. 41, 61, 123-124
- ^ O'Neill 2006, б. 395
- ^ Хелгасон 1978 ж, б. 92
- ^ O'Neill 2006, б. 286
- ^ do Carmo 2016, б. 227
- ^ Osserman 2002, 31-32 бет
- ^ а б c Eisenhart 2004
- ^ do Carmo 2016, pp. 283-286
- ^ Thorpe 1994, pp. 201-207
- ^ Singer & Thorpe 1967; Garsia, Adriano M. (1961), "An imbedding of closed Riemann surfaces in Euclidean space", Түсініктеме. Математика. Хельв., 35: 93–110, дои:10.1007/BF02567009
- ^ Имаоши және Танигучи 1992 ж, 47-49 беттер
- ^ Berger 1977; Тейлор 1996.
- ^ Уилсон 2008, pp. 1–23, Chapter I, Евклидтік геометрия.
- ^ do Carmo 2016.
- ^ Уилсон 2008, pp. 25–49, Chapter II, Сфералық геометрия.
- ^ Уилсон 2008, 2 тарау.
- ^ Eisenhart 2004, б. 110.
- ^ Stillwell 1990; Bonola, Carslaw & Enriques 1955.
- ^ Уилсон 2008, 5 тарау.
- ^ Taylor 1996b, б. 107; Berger 1977, 341-343 бб.
- ^ Berger 1977, pp. 222–225; Taylor 1996b, pp. 101–108.
- ^ Taylor 1996b
- ^ Chow 1991
- ^ Chen, Lu & Tian (2006) pointed out and corrected a missing step in the approach of Hamilton and Chow; қараңыз Andrews & Bryan (2009).
- ^ Eisenhart 2004; Kreyszig 1991; Бергер 2004; Уилсон 2008.
- ^ Кобаяши және Номизу 1969 ж, XII тарау.
- ^ do Carmo 2016; O'Neill 2006; Singer & Thorpe 1967.
- ^ Levi-Civita 1917
- ^ Арнольд 1989 ж, pp. 301–306, Appendix I.; Бергер 2004, 263–264 беттер.
- ^ Дарбу.
- ^ Кобаяши және Номизу 1969 ж
- ^ Ivey & Landsberg 2003.
- ^ Бергер 2004, pp. 145–161; do Carmo 2016; Chern 1967; Hopf 1989.
- ^ Codá Marques, Fernando; Невес, Андре (2014). "Min-Max theory and the Willmore conjecture". Математика жылнамалары. 179 (2): 683–782. arXiv:1202.6036. дои:10.4007 / жылнамалар.2014.179.2.6. JSTOR 24522767.
- ^ Rotman, R. (2006) "The length of a shortest closed geodesic and the area of a 2-dimensional sphere", Proc. Amer. Математика. Soc. 134: 3041-3047. Previous lower bounds had been obtained by Croke, Rotman-Nabutovsky and Sabourau.
Әдебиеттер тізімі
- Эндрюс, Бен; Брайан, Пол (2010), «Екі сферадағы нормаланған Риччи ағыны үшін изопериметриялық салыстыру арқылы қисықтық шекаралары», Кальц. Var. Жартылай дифференциалдық теңдеулер, 39 (3–4): 419–428, arXiv:0908.3606, дои:10.1007 / s00526-010-0315-5
- Арнольд, В.И. (1989), Классикалық механиканың математикалық әдістері, Математика бойынша магистратура мәтіндері, 60 (2-ші басылым), Нью-Йорк: Спрингер-Верлаг, ISBN 978-0-387-90314-9; translated from the Russian by K. Vogtmann and A. Weinstein.
- Бергер, Марсель (2004), A Panoramic View of Riemannian Geometry, Springer-Verlag, ISBN 978-3-540-65317-2
- Бергер, Мелвин С. (1977), Nonlinearity and Functional Analysis, Academic Press, ISBN 978-0-12-090350-4
- Bonola, Roberto; Carslaw, H. S.; Enriques, F. (1955), Non-Euclidean Geometry: A Critical and Historical Study of Its Development, Довер, ISBN 978-0-486-60027-7
- Boothby, William M. (1986), Дифференциалды коллекторлар мен Риман геометриясына кіріспе, Pure and Applied Mathematics, 120 (2-ші басылым), Academic Press, ISBN 0121160521
- Картан, Эли (1983), Риман кеңістігінің геометриясы, Математикалық ғылыми басылым, ISBN 978-0-915692-34-7; translated from 2nd edition of Leçons sur la géométrie des espaces de Riemann (1951) by James Glazebrook.
- Картан, Эли (2001), Riemannian Geometry in an Orthogonal Frame (from lectures delivered by É Cartan at the Sorbonne in 1926-27) (PDF), Әлемдік ғылыми, ISBN 978-981-02-4746-1[өлі сілтеме ]; translated from Russian by V. V. Goldberg with a foreword by С. Черн.
- Cartan, Henri (1971), Калифорния (француз тілінде), Герман, ISBN 9780395120330
- Чен, Сюсюонг; Лу, Пенг; Тянь, Банг (2006), «Риманның беттерін Ricci ағынымен біркелкі ету туралы жазба», Proc. БАЖ, 134 (11): 3391–3393, дои:10.1090 / S0002-9939-06-08360-2
- Черн, С. (1967), Curves and Surfaces in Euclidean Spaces, MAA Studies in Mathematics, Mathematical Association of America
- Chow, B. (1991), "The Ricci flow on a 2-sphere", Дж. Дифф. Геом., 33 (2): 325–334, дои:10.4310 / jdg / 1214446319
- Курант, Ричард (1950), Dirichlet's Principle, Conformal Mapping and Minimal Surfaces, Джон Вили және ұлдары, ISBN 978-0-486-44552-6
- Дарбу, Гастон, Leçons sur la théorie générale des surfaces, Готье-Вилларс Volume I (1887), Volume II (1915) [1889], Volume III (1894), Volume IV (1896).
- Ding, W. (2001), "A proof of the uniformization theorem on S2", J. Partial Differential Equations, 14: 247–250
- Кармо, Манфредо П. (2016), Қисықтар мен беттердің дифференциалды геометриясы (revised & updated 2nd ed.), Mineola, NY: Dover Publications, Inc., ISBN 0-486-80699-5
- Кармо, Манфредо (1992), Риман геометриясы, Mathematics: Theory & Applications, Birkhäuser, ISBN 0-8176-3490-8
- Eisenhart, Luther Pfahler (2004), Қисықтар мен беттердің дифференциалды геометриясы туралы трактат (reprint of the 1909 ed.), Dover Publications, Inc., ISBN 0-486-43820-1
- Эйлер, Леонхард (1760), "Recherches sur la courbure des surfaces", Mémoires de l'Académie des Sciences de Berlin (published 1767), 16: 119–143.
- Эйлер, Леонхард (1771), "De solidis quorum superficiem in planum explicare licet", Novi Commentarii Academiae Scientiarum Petropolitanae (published 1772), 16: 3–34.
- Гаусс, Карл Фридрих (1902), General Investigations of Curved Surfaces of 1825 and 1827, Принстон университетінің кітапханасы аударған А.М. Hiltebeitel and J.C. Morehead; "Disquisitiones generales circa superficies curvas", Commentationes Societatis Regiae Scientiarum Gottingesis Recentiores Том. VI (1827), pp. 99–146.
- Gauss, Carl Friedrich (1965), Қисық беттерді жалпы зерттеу, аударған А.М. Hiltebeitel; J.C. Morehead, Hewlett, NY: Raven Press, OCLC 228665499.
- Gauss, Carl Friedrich (2005), Қисық беттерді жалпы зерттеу, editted with a new introduction and notes by Peter Pesic, Mineola, NY: Dover Publications, ISBN 978-0-486-44645-5.
- Gray, Alfred; Abbena, Elsa; Salamon, Simon (2006), Modern Differential Geometry of Curves And Surfaces With Mathematica®, Studies in Advanced Mathematics (3rd ed.), Boca Raton, FL: Chapman & Hall/CRC, ISBN 978-1-58488-448-4
- Хан, Цин; Hong, Jia-Xing (2006), Isometric Embedding of Riemannian Manifolds in Euclidean Spaces, Американдық математикалық қоғам, ISBN 978-0-8218-4071-9
- Гельгасон, Сигурдур (1978), Differential Geometry,Lie Groups, and Symmetric Spaces, Academic Press, Нью-Йорк, ISBN 978-0-12-338460-7
- Хилберт, Дэвид; Кон-Воссен, Стефан (1952), Геометрия және қиял (2nd ed.), New York: Chelsea, ISBN 978-0-8284-1087-8
- Хитчин, Найджел (2013), Geometry of Surfaces (PDF)
- Hopf, Heinz (1989), Lectures on Differential Geometry in the Large, Математикадан дәрістер, 1000, Springer-Verlag, ISBN 978-3-540-51497-8
- Имайоши, Ю .; Танигучи, М. (1992), An Introduction to Techmüller spaces, Springer-Verlag, ISBN 978-0-387-70088-5
- Ivey, Thomas A.; Landsberg, J.M. (2003), Cartan for Beginners: Differential Geometry via Moving Frames and Exterior Systems, Математика бойынша магистратура, 61, Американдық математикалық қоғам, ISBN 978-0-8218-3375-9
- Катц, Михаил Г. (2007), Systolic geometry and topology, Mathematical Surveys and Monographs, 137, Американдық математикалық қоғам, ISBN 978-0-8218-4177-8
- Kobayashi, Shoshichi (1956), "Induced connections and imbedded Riemannian space", Нагоя математикасы. Дж., 10: 15–25, дои:10.1017/S0027763000000052
- Кобаяши, Шошичи (1957), "Theory of connections", Annali di Matematica Pure ed Applicata, 4 серия, 43: 119–194, дои:10.1007 / BF02411907,
- Кобаяши, Шошичи; Номизу, Катсуми (1963), Дифференциалдық геометрияның негіздері, т. Мен, Вили Интерсианс, ISBN 978-0-470-49648-0
- Кобаяши, Шошичи; Номизу, Катсуми (1969), Дифференциалдық геометрияның негіздері, т. II, Вили Интерсианс, ISBN 978-0-470-49648-0
- Крейциг, Эрвин (1991), Дифференциалдық геометрия, Довер, ISBN 978-0-486-66721-8
- Kühnel, Wolfgang (2006), Дифференциалдық геометрия: қисықтар - беттер - көп қатпарлы, Американдық математикалық қоғам, ISBN 978-0-8218-3988-1
- Levi-Civita, Tullio (1917), «Nozione di parallelismo in una varietà qualunque» (PDF), Көрсету. Circ. Мат Палермо, 42: 173–205, дои:10.1007/BF03014898
- O'Neill, Barrett (2006), Elementary Differential Geometry (revised 2nd ed.), Amsterdam: Elsevier/Academic Press, ISBN 0-12-088735-5
- Осгуд, Б .; Филлипс, Р .; Сарнак, П. (1988), «Лаплациандардың детерминанттарының экстремалдары», Дж. Функт. Анал., 80: 148–211, дои:10.1016/0022-1236(88)90070-5
- Osserman, Robert (2002), Минималды беттерді зерттеу, Довер, ISBN 978-0-486-49514-9
- Ян Р. (2001) Geometric Differentiation: for the intelligence of curves and surfaces, Кембридж университетінің баспасы ISBN 0-521-00264-8.
- Pressley, Andrew (2001), Elementary Differential Geometry, Springer Undergraduate Mathematics Series, Springer-Verlag, ISBN 978-1-85233-152-8
- Қаптар, Дж .; Uhlenbeck, Karen (1981), "The existence of minimal immersions of 2-spheres", Энн. математика, 112 (1): 1–24, дои:10.2307/1971131, JSTOR 1971131
- Әнші, Исадор М.; Thorpe, John A. (1967), Lecture Notes on Elementary Topology and Geometry, Springer-Verlag, ISBN 978-0-387-90202-9
- Спивак, Майкл (1965), Коллекторлы есептеу. Жетілдірілген есептеудің классикалық теоремаларына заманауи көзқарасБенджамин
- Stillwell, John (1996), Гиперболалық геометрияның қайнар көздері, Американдық математикалық қоғам, ISBN 978-0-8218-0558-9
- Struik, Dirk (1987), Математиканың қысқаша тарихы (4th ed.), Dover Publications, ISBN 0486602559
- Струк, Дирк Дж. (1988), Lectures on Classical Differential Geometry (reprint of 2nd ed.), New York: Dover Publications, Inc., ISBN 0-486-65609-8
- Тейлор, Майкл Э. (1996a), Partial Differential Equations II: Qualitative Studies of Linear Equations, Springer-Verlag, ISBN 978-1-4419-7051-0
- Тейлор, Майкл Э. (1996b), Partial Differential Equations III: Nonlinear equations, Springer-Verlag, ISBN 978-1-4419-7048-0
- Thorpe, John A. (1994), Elementary topics in differential geometry, Undergraduate Texts in Mathematics, Springer-Verlag, ISBN 0387903577
- Toponogov, Victor A. (2005), Differential Geometry of Curves and Surfaces: A Concise Guide, Springer-Verlag, ISBN 978-0-8176-4384-3
- Valiron, Georges (1986), The Classical Differential Geometry of Curves and Surfaces, Математикалық ғылыми басылым, ISBN 978-0-915692-39-2 Full text of book
- Уорнер, Фрэнк В. (1983), Дифференциалданатын коллекторлар мен Lie топтарының негіздері, Математика бойынша магистратура мәтіндері, 94, Springer, ISBN 0-387-90894-3
- Wells, R. O. (2017), Differential and complex geometry: origins, abstractions and embeddings, Springer, ISBN 9783319581842
- Wilson, Pelham (2008), Curved Space: From Classical Geometries to Elementary Differential Geometry, Кембридж университетінің баспасы, ISBN 978-0-521-71390-0
Сыртқы сілтемелер
 Қатысты медиа Беттердің дифференциалды геометриясы Wikimedia Commons сайтында
Қатысты медиа Беттердің дифференциалды геометриясы Wikimedia Commons сайтында





















![{ displaystyle [X, Y] = XY-YX}](https://wikimedia.org/api/rest_v1/media/math/render/svg/838f73010b4f791eeaf245317fb4b6e07c45d741)
![[X, Y]](https://wikimedia.org/api/rest_v1/media/math/render/svg/94470b44d283fde62130212956058ca6b727da37)
![{ displaystyle [X, Y] = - [Y, X]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8c433e248c0c7e659ef3f2d9df64d8c7505630bc)
![{ displaystyle [[X, Y], Z] + [[Y, Z], X] + [[Z, X], Y] = 0.]](https://wikimedia.org/api/rest_v1/media/math/render/svg/a4d5d5018bd0a276d74259b92a5403824cd982e7)













































































![{ displaystyle K = - { beta ^ {2} over ((s- alpha) ^ {2} + beta ^ {2}) ^ {2}}, , , K_ {m} = - {r [(s- alpha) ^ {2} + beta ^ {2})] + beta _ {t} (s- alpha) + beta alpha _ {t} over [(s-) альфа) ^ {2} + бета ^ {2}] ^ { frac {3} {2}}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ff1ab2130e1d570ae5585c216637fb7661847192)








![{ displaystyle K = - {1 2H} үстінде сол жақта [ ішінара _ {x} сол жақта ({ frac {G_ {x}} {H}} оң) + іштей _ {у} сол жақта ( { frac {E_ {y}} {H}} right) right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fa6e6e49b1e0f474132e77018b4d8a8fc78a853d)

































