Аффиндік байланыс - Affine connection
Бұл мақалада жалпы тізімі бар сілтемелер, бірақ бұл негізінен тексерілмеген болып қалады, өйткені ол сәйкесінше жетіспейді кірістірілген дәйексөздер. (Ақпан 2017) (Бұл шаблон хабарламасын қалай және қашан жою керектігін біліп алыңыз) |

Жылы Дифференциалды геометрия, an аффиндік байланыс геометриялық объект болып табылады тегіс коллектор қайсысы қосады Жақын жанас кеңістіктер, сондықтан бұл мүмкіндік береді жанама векторлық өрістер болу сараланған олар манифольдтегі функциялары бекітілгендей векторлық кеңістік. Аффиналық байланыс ұғымы 19 ғасырдың геометриясында және тензор есебі, бірақ 1920 жылдың басына дейін толығымен дамымаған болатын Эли Картан (оның жалпы теориясының бөлігі ретінде байланыстар ) және Герман Вейл (кім бұл ұғымды өзінің негіздерінің бөлігі ретінде қолданды жалпы салыстырмалылық ). Терминология Картанға байланысты және оның жанама кеңістіктерді анықтаудан бастау алады Евклид кеңістігі Rn аударма арқылы: аффиндік байланысты таңдау көп қырлы эвклид кеңістігі сияқты тегіс емес, сонымен қатар аффиналық кеңістік.
Кез-келген оң өлшемнің көптеген аффиналық байланыстары бар. Егер коллектор одан әрі а-мен жабдықталған болса Риман метрикасы онда аффиндік байланыстың табиғи таңдауы бар, деп аталады Levi-Civita байланысы. Аффиндік байланысты таңдау бірнеше негізделген қасиеттерді қанағаттандыратын векторлық өрістерді дифференциалдау тәсілін тағайындауға тең (сызықтық және Лейбниц ережесі ). Бұл аффиндік байланыстың а деген анықтамасын береді ковариант туынды немесе (сызықтық) байланыс үстінде тангенс байламы. Аффиндік байланысты таңдау да ұғымына балама параллель тасымалдау, бұл жанама векторларды қисық бойымен тасымалдау әдісі. Бұл сонымен қатар параллельді тасымалдауды анықтайды жақтау байламы. Рамалық байламдағы шексіз параллель тасымалдау аффиндік байланыстың тағы бір сипаттамасын береді, немесе а түрінде Картандық байланыс үшін аффиндік топ немесе а негізгі байланыс жақтау байламында.
Аффиналық байланыстың негізгі инварианттары оның бұралу және оның қисықтық. Бұралу қаншалықты тығыз екенін өлшейді Жалған жақша векторлық өрістерді аффиндік байланыс арқылы қалпына келтіруге болады. Аффиндік қосылыстарды анықтау үшін де қолданылуы мүмкін (аффиндік) геодезия жалпылай отырып, коллекторда түзу сызықтар Евклид кеңістігі, дегенмен бұл түзулердің геометриясы әдеттегіден өзгеше болуы мүмкін Евклидтік геометрия; негізгі айырмашылықтар байланыстың қисаюына инкапсуляцияланған.
Мотивация және тарих
A тегіс коллектор Бұл математикалық жергілікті нысанда евклид кеңістігінің тегіс деформациясы сияқты көрінеді Rn: мысалы, тегіс қисық немесе бет жергілікті сызықтың немесе жазықтықтың тегіс деформациясы сияқты көрінеді. Тегіс функциялар және векторлық өрістер Евклид кеңістігінде сияқты коллекторларда анықталуы мүмкін және скаляр коллекторлардағы функцияларды табиғи түрде ажыратуға болады. Алайда, векторлық өрістерді дифференциациялау оңай емес: бұл Евклид кеңістігіндегі қарапайым мәселе, өйткені базалық векторлардың жанасу кеңістігі нүктеде б жанындағы кеңістіктегі жанама кеңістікпен табиғи түрде (аударма арқылы) анықталуы мүмкін q. Жалпы коллекторда жақын жанама кеңістіктер арасында мұндай табиғи идентификация жоқ, сондықтан жақын нүктелердегі жанамалы векторларды дәл анықталған әдіспен салыстыруға болмайды. Аффиналық байланыс ұғымы осы мәселені шешу үшін енгізілген байланыстырушы жанасатын кеңістіктер. Бұл идеяның бастауы екі негізгі дереккөзден бастау алады: беттік теория және тензор есебі.
Беттік теорияның мотивациясы
Тегіс бетті қарастырыңыз S үш өлшемді эвклид кеңістігінде. Кез-келген нүктеге жақын, S оның көмегімен жуықтауға болады жанама жазықтық сол кезде, яғни аффиндік кеңістік Евклид кеңістігінің. 19 ғасырдағы дифференциалды геометрлерді ұғымы қызықтырды даму онда бір бет болды шиыршықталған басқа бойымен, онсыз сырғанау немесе бұралу. Атап айтқанда, жанама жазықтық S айналдыруға болады S: бұл қашан болатынын елестету оңай болуы керек S а-ның тегіс шекарасы болатын 2-сфера сияқты бет дөңес аймақ. Тангенс жазықтығы домаланған кезде S, байланыс нүктесі қисық сызықты анықтайды S. Керісінше, қисығы берілген S, жанама жазықтықты сол қисық бойымен айналдыруға болады. Бұл қисық бойымен әр түрлі нүктелердегі жанама жазықтықтарды анықтау әдісін ұсынады: атап айтқанда, қисықтың бір нүктесіндегі жанасу кеңістігіндегі жанасу векторы қисықтың кез келген басқа нүктесінде ерекше жанама вектормен анықталады. Бұл сәйкестендіру әрдайым беріледі аффиналық түрленулер жанасу жазықтығынан екіншісіне.
Тангенс векторларын аффиналық түрлендірулер арқылы қисық бойымен параллель тасымалдау туралы түсінік тән сипаттамаға ие: жанасатын жазықтықтың бетімен жанасу нүктесі. әрқашан қозғалады параллель трансляциядағы қисықпен (яғни, жанама жазықтық бет бойымен домалақталған кезде жанасу нүктесі қозғалады). Бұл жалпы жағдай тән Картандық байланыстар. Қазіргі заманғы тәсілдерде байланыс нүктесі ретінде қарастырылады шығу тегі жанамалы жазықтықта (ол векторлық кеңістік болады), ал шығу тегі қозғалысы аудармамен түзетіледі, осылайша параллель тасымалдау аффинді емес, сызықты болады.
Картандық байланыстар тұрғысынан Евклид кеңістігінің аффиндік ішкі кеңістігі болып табылады модель беттер - олар Евклидтік-3 кеңістігіндегі ең қарапайым беттер және жазықтықтың аффиндік тобы бойынша біртектес - және әр тегіс беттің әр нүктесінде оған жанама моделінің ерекше моделі болады. Бұл модель беттері Клейн геометриясы мағынасында Феликс Клейн Келіңіздер Эрланген бағдарламасы. Жалпы, ан n-өлшемді аффиналық кеңістік - бұл а Клейн геометриясы үшін аффиндік топ Афф (n), нүктенің тұрақтандырғышы жалпы сызықтық топ GL (n). Аффин n-манифольд шексіз ұқсас коллектор болып табылады n-өлшемді аффиналық кеңістік.
Тензор есебінен мотивация
Аффиналық байланыстардың екінші мотиві а ұғымынан туындайды ковариант туынды өрістердің векторлары. Координаттардан тәуелсіз әдістер пайда болғанға дейін, арқылы векторлық өрістермен жұмыс істеу керек болды ендіру олардың сәйкесінше Евклидтік векторлар ішіне атлас. Бұл компоненттерді ажыратуға болады, бірақ туындылар координаталардың өзгеруі кезінде басқарылатын тәсілмен өзгермейді.[дәйексөз қажет ] Түзету шарттары енгізілді Элвин Бруно Кристоффель (келесі идеялар Бернхард Риман ) 1870 жылдары бір векторлық өрістің екіншісі бойымен (түзетілген) туындысы өзгергендей болды ковариантты координаталық түрлендірулер кезінде - бұл түзету шарттары кейіннен белгілі болды Christoffel рәміздері.
Бұл идея теориясына айналды абсолютті дифференциалдық есептеу (қазір белгілі тензор есебі ) арқылы Грегорио Риччи-Кербастро және оның оқушысы Туллио Леви-Сивита 1880 жыл мен 20 ғасырдың бас кезінде.
Тензорлық есептеу шынымен өмірге келді, дегенмен, пайда болды Альберт Эйнштейн теориясы жалпы салыстырмалылық 1915 жылы. Осыдан бірнеше жыл өткен соң, Леви-Сивита Риман метрикасымен байланысты бірегей байланысты рәсімдеді, қазір ол Levi-Civita байланысы. 1920 жылы шамамен жалпы аффиндік байланыстар зерттелді Герман Вейл,[1] жалпы салыстырмалылықтың егжей-тегжейлі математикалық негізін жасаған және Эли Картан,[2] беттік теориядан шыққан геометриялық идеялармен байланыстырған кім.
Тәсілдер
Кешенді тарих аффиндік байланыс тұжырымдамасына кеңінен түрліше көзқарастар мен тұжырымдамалардың дамуына әкелді.
Ең танымал тәсіл - бұл ковариантты туындыларға негізделген анықтама. Бір жағынан, Вейлдің идеяларын физиктер формасында қабылдады калибр теориясы және ковариант туындыларын өлшеу. Екінші жағынан, ковариантты саралау ұғымы абстрактілі болды Жан-Луи Косзул, кім анықтады (сызықтық немесе Қосзул) байланыстар қосулы байламдар. Бұл тілде аффиндік байланыс жай а ковариант туынды немесе (сызықтық) байланыс үстінде тангенс байламы.
Алайда, бұл тәсіл аффиндік байланыстардың геометриясын және олардың өз аттарын қалай алғанын түсіндірмейді.[a] Термин шын мәнінде евклид кеңістігіндегі жанама кеңістікті аударма арқылы анықтаудан бастау алады: бұл қасиет евклидтік дегенді білдіреді n-кеңістік - бұл аффиналық кеңістік. (Сонымен қатар, Евклид кеңістігі - а негізгі біртекті кеңістік немесе торсор аффиндік топтың кіші тобы болып табылатын аудармалар тобына жатады.) Кіріспеде айтылғандай, мұны дәлдеудің бірнеше әдісі бар: аффиндік байланыс деген ұғымды анықтайтын фактіні пайдаланады параллель тасымалдау қисық бойындағы векторлық өрістер. Бұл сонымен қатар параллельді тасымалдауды анықтайды жақтау байламы. Рамалық байламдағы шексіз параллель тасымалдау аффиндік байланыстың тағы бір сипаттамасын береді, аффиндік топ үшін картандық байланыс ретінде Афф (n) немесе директор ретінде GL (n) жақтау байламындағы байланыс.
Дифференциалдық оператор ретіндегі формальды анықтама
Келіңіздер М тегіс болыңыз көпжақты және рұқсат етіңіз Γ (ТМ) кеңістігі векторлық өрістер қосулы М, яғни кеңістігі тегіс бөлімдер туралы тангенс байламы ТМ. Содан кейін аффиндік байланыс қосулы М Бұл екі сызықты карта
барлық тегіс функциялар үшін f жылы C∞(М, R) және барлық векторлық өрістер X, Y қосулы М:
- ∇fXY = f ∇XY, Бұл, ∇ болып табылады C∞(М, R)-сызықтық бірінші айнымалыда;
- ∇X( fY ) = df (X)Y + f ∇XY, Бұл, ∇ қанағаттандырады Лейбниц ережесі екінші айнымалыда.
Элементтік қасиеттер
- Жоғарыдағы 1-қасиеттен -ның мәні шығады ∇XY бір сәтте х ∈ М мәніне ғана байланысты X кезінде х және мәні бойынша емес X қосулы М − {х}. Сондай-ақ, жоғарыдағы 2-қасиеттен -нің мәні шығады ∇XY бір сәтте х ∈ М мәніне ғана байланысты Y маңында х.
- Егер ∇1, ∇2 аффиндік қосылыстар болып табылады, содан кейін мәні х туралы ∇1
XY − ∇2
XY жазылуы мүмкін Γх(Xх, Yх) қайда
- айқын және тәуелді х (яғни, ол тегістігін анықтайды шумақ гомоморфизмі ). Керісінше болса ∇ аффиндік байланыс және Γ осындай тегіс білезік шоғыры гомоморфизм (а деп аталады байланыс формасы қосулы М) содан кейін ∇ + Γ аффиндік байланыс.
- Егер М ашық ішкі жиыны болып табылады Rn, содан кейін тангенс байламы М болып табылады тривиальды байлам М × Rn. Бұл жағдайда канондық аффиндік байланыс бар г. қосулы М: кез-келген векторлық өріс Y тегіс функциямен беріледі V бастап М дейін Rn; содан кейін г.XY - тегіс функцияға сәйкес келетін векторлық өріс г.V(X) = ∂XY бастап М дейін Rn. Кез-келген басқа аффиндік байланыс ∇ қосулы М сондықтан жазылуы мүмкін ∇ = d + Γ, қайда Γ байланыс формасы болып табылады М.
- Жалпы, а жергілікті тривиализация тангенс байламы - а байламның изоморфизмі арасындағы шектеу ТМ ашық ішкі жиынға U туралы М, және U × Rn. Аффиндік байланысты шектеу ∇ дейін U түрінде жазылуы мүмкін d + Γ қайда Γ байланыс формасы болып табылады U.
Аффиндік қосылыстар үшін параллель тасымалдау
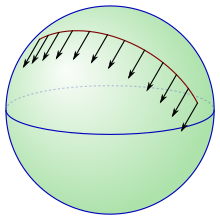
Жанама векторларды коллектордың әр түрлі нүктелерінде салыстыру, әдетте, нақты анықталған процесс емес. Аффиндік байланыс мұны түсініктің көмегімен жоюдың бір әдісін ұсынады параллель тасымалдау, және шынымен де бұл аффиндік байланыстың анықтамасын беру үшін қолданыла алады.
Келіңіздер М аффиндік байланысы бар коллектор болыңыз ∇. Содан кейін векторлық өріс X деп айтылады параллель егер ∇X = 0 кез-келген векторлық өріс үшін деген мағынада Y, ∇YX = 0. Параллель векторлар интуитивті түрде айтылады олардың бәрі туындылар нөлге тең сондықтан кейбір мағынада тұрақты. Параллель векторлық өрісті екі нүктеде бағалау арқылы х және ж, at жанама векторының арасындағы сәйкестендіру х және біреуі ж алынды. Мұндай жанама векторлар деп аталады параллель көліктер бір-бірінің.
Нөлдік емес параллель векторлық өрістер, жалпы, жоқ, өйткені теңдеу ∇X = 0 Бұл дербес дифференциалдық теңдеу қайсысы анықталған: интегралдау шарты өйткені бұл теңдеудің жойылуы қисықтық туралы ∇ (төменде қараңыз). Алайда, егер бұл теңдеу а-мен шектелген болса қисық бастап х дейін ж ол болады қарапайым дифференциалдық теңдеу. Содан кейін кез келген бастапқы мәні үшін ерекше шешім бар X кезінде х.
Дәлірек айтқанда, егер γ : Мен → М а тегіс қисық интервалмен параметрленген [а, б] және ξ . ТхМ, қайда х = γ(а), содан кейін а векторлық өріс X бойымен γ (және, атап айтқанда, осы векторлық өрістің мәні ж = γ(б)) деп аталады параллель тасымалдау ξ бойымен γ егер
- ∇γ ′(т)X = 0, барлығына т ∈ [а, б]
- Xγ(а) = ξ.
Формальды түрде бірінші шарт осыны білдіреді X қатысты параллель кері тарту үстінде байлам γ . ТМ. Алайда, а жергілікті тривиализация бұл бірінші ретті жүйе сызықтық қарапайым дифференциалдық теңдеулер, онда екінші шартпен берілген кез-келген бастапқы шарт үшін ерекше шешім бар (мысалы, Пикард - Линделёф теоремасы ).
Осылайша параллельді тасымалдау интуитивті мағынада оларды «бір бағытқа бағыттайтын» етіп ұстау үшін аффиналық байланыстың көмегімен қисық бойымен жанама векторларды қозғалту тәсілін ұсынады және бұл сызықтық изоморфизм қисықтың екі ұшындағы жанама кеңістіктер арасында. Осылайша алынған изоморфизм жалпы алғанда қисықты таңдауға байланысты болады: егер олай болмаса, онда параллель векторлық өрістерді анықтау үшін әрбір қисық бойымен параллель тасымалдауды қолдануға болады. М, егер бұл қисықтық болса ғана орын алуы мүмкін ∇ нөлге тең.
Сызықтық изоморфизм оның ан-ға әсер етуімен анықталады тапсырыс берілген негіз немесе жақтау. Демек, параллель тасымалдауды элементтерді (тангенс) тасымалдау тәсілі ретінде де сипаттауға болады. жақтау байламы GL (М) қисық бойымен. Басқаша айтқанда, аффиндік байланыс а көтеру кез келген қисықтың γ жылы М қисыққа γ̃ жылы GL (М).
Рамалық байламдағы формальды анықтама
Аффиндік байланыс а ретінде анықталуы мүмкін негізгі GL (n) байланыс ω үстінде жақтау байламы FМ немесе GL (М) коллектордың М. Толығырақ, ω тангенс байламынан тегіс карта T (FМ) жақтау байламының кеңістігіне n × n матрицалар (бұл Алгебра gl(n) туралы Өтірік тобы GL (n) аударылатын n × n матрицалар) екі қасиетті қанағаттандырады:
- ω болып табылады эквивариант әрекетіне қатысты GL (n) қосулы T (FМ) және gl(n);
- ω(Xξ) = ξ кез келген үшін ξ жылы gl(n), қайда Xξ - векторлық өріс FМ сәйкес ξ.
Мұндай байланыс ω бірден анықтайды ковариант туынды жанасатын байламда ғана емес, сонымен қатар байламдар байланысты кез келгенге топтық өкілдік туралы GL (n)бумаларын қосқанда тензорлар және тензор тығыздығы. Керісінше, тангенс байламындағы аффиндік жалғау, мысалы, рамка байламындағы аффиндік байланысты анықтайды, ω жанама векторларда параллель тасымалдаумен анықталған рамалық шоғырға қисықтарды көтеруге дейін жоғалады.
Рамалық байлам а дәнекерлеу формасы θ : T (FМ) → Rn қайсысы көлденең ол жоғалады деген мағынада тік векторлар векторлық өрістердің нүктелік мәндері сияқты Xξ: Әрине θ алдымен жанама векторды проекциялау арқылы анықталады (-ге FМ жақтауда f) дейін М, содан кейін осы жанама вектордың компоненттерін қабылдау арқылы М жақтауға қатысты f. Ескертіп қой θ сонымен қатар GL (n)- эквивалент (қайда GL (n) әрекет етеді Rn матрицалық көбейту арқылы).
Жұп (θ, ω) анықтайды а байламның изоморфизмі туралы T (FМ) тривиальды байламмен FМ × афф(n), қайда афф(n) болып табылады Декарттық өнім туралы Rn және gl(n) (аффин тобының Lie алгебрасы ретінде қарастырылады, ол шын мәнінде а жартылай бағыт өнім - төменде қараңыз).
Аффиндік қосылыстар картандық байланыстар ретінде
Аффиндік байланыстарды Картанның жалпы шеңберінде анықтауға болады.[3] Заманауи тәсілде бұл рамалық байламдағы аффиндік байланыстарды анықтаумен тығыз байланысты. Шынында да, бір тұжырымда Картан байланысы абсолютті параллелизм қолайлы қасиеттерді қанағаттандыратын негізгі байлам. Осы тұрғыдан алғанда афф(n)- бір форма бойынша бағаланады (θ, ω): T (FМ) → афф(n) жақтау байламында аффиндік коллектор ) картандық байланыс. Алайда, Картанның алғашқы тәсілі бірнеше тәсілдермен ерекшеленді:
- рамалық байламдар немесе негізгі байламдар туралы түсінік болмаған;
- байланыс шексіз жақын нүктелер арасындағы параллель тасымалдау тұрғысынан қарастырылды;[b]
- бұл параллель тасымалдау сызықты емес, аффинді болды;
- тасымалданатын объектілер қазіргі мағынада жанама векторлар емес, ан элементтері болды аффиналық кеңістік түпнұсқа Cartan байланысы бар белгіленген нүктемен анықтайды жанасу кеңістігімен.
Түсініктемелер және тарихи түйсік
Жаңа көтерілген ұпайларды беттік теория ұсынған мотивациядан бастап, керісінше түсіндіру оңай. Бұл жағдайда, үстіңгі бетке домалап жатқан жазықтықтар аңғал мағынада жанасатын жазықтықтар болғанымен, жанасу кеңістігі шынымен де шексіз түсінік,[c] ал ұшақтар аффиндік ішкі кеңістіктер туралы R3, болып табылады шексіз дәрежеде. Алайда бұл аффиндік жазықтықтардың барлығының белгіленген нүктесі, бетімен жанасу нүктесі бар және олар осы кезде бетке жанасады. Сондықтан шатасуы белгіленген нүктесі бар аффиналық кеңістікті сол кездегі тангенс кеңістігімен анықтауға болатындықтан туындайды. Алайда, илектеу арқылы анықталған параллель тасымалдау осы бастауды түзетпейді: ол аффин сызықтық емес; сызықтық параллель тасымалдауды аударманы қолдану арқылы қалпына келтіруге болады.
Осы ойды тұжырымдап, аффиндік коллектор ан болуы керек n-көпқабатты М аффинді кеңістікпен Aх, өлшем n, тіркелген әрқайсысына х ∈ М белгіленген жерде ах ∈ Aх, осы аффиналық кеңістіктердің элементтерін кез-келген қисық бойымен тасымалдау әдісімен бірге C жылы М. Бұл әдіс бірнеше қасиеттерді қанағаттандыру үшін қажет:
- кез келген екі ұпай үшін х, ж қосулы C, параллель тасымалдау аффиналық трансформация бастап Aх дейін Aж;
- параллель тасымалдау кез келген сәтте дифференциалданатын мағынасында шексіз анықталады C және тек жанама векторға тәуелді C сол кезде;
- кезінде параллель тасымалдаудың туындысы х анықтайды сызықтық изоморфизм бастап ТхМ дейін ТахAх.
Соңғы екі тармақты дәл анықтау қиын,[5] сондықтан аффиндік байланыстар көбінесе шексіз анықталады. Мұны ынталандыру үшін аффинді қарастыру жеткілікті анықтамалық шеңберлер параллель тасымалдауға қатысты шексіз түрлендіру. (Cartan's бастауы осында кадрларды жылжыту әдісі.) Аффиналық фрейм нүктеден тұрады (б, e1,… en), қайда б ∈ Aх[d] және eмен негізін құрайды Тб(Aх). Одан кейін аффиндік байланыс символдық түрде бірінші реттік беріледі дифференциалдық жүйе
жиынтығымен анықталған бір формалы (θj, ωj
мен). Геометриялық түрде аффиналық рамка қисық бойымен қозғалатын орын ауыстыруға ұшырайды γ бастап γ(т) дейін γ(т + δt) берілген (шамамен, немесе шексіз)
Сонымен қатар аффиналық кеңістіктер Aх тангенстің болуы талап етіледі М ауыстыру деген бейресми мағынада ах бойымен γ тангенс векторымен (шамамен немесе шексіз) анықталуы мүмкін γ′(т) дейін γ кезінде х = γ(т) (бұл шексіз жылжу х). Бастап
қайда θ арқылы анықталады θ(X) = θ1(X)e1 + … + θn(X)en, бұл сәйкестендіру θ, сондықтан талап сол θ әр нүктеде сызықтық изоморфизм болуы керек.
Тангенциалдық аффиналық кеңістік Aх осылайша интуитивті түрде анықталады шексіз аффиндік көршілік туралы х.
Заманауи көзқарас негізгі түйіндерді қолдану арқылы түйсіктің бәрін дәлірек етеді (маңызды идея - кадрды немесе жақтауды ауыстыру айнымалы осы кеңістіктегі барлық кадрлар мен функциялардың кеңістігі бойынша кадр). Бұл сонымен бірге шабытына сүйенеді Феликс Клейн Келіңіздер Эрланген бағдарламасы,[6] онда а геометрия а деп анықталған біртекті кеңістік. Аффин кеңістігі осы мағынада геометрия болып табылады және а жалпақ Картандық байланыс. Осылайша, жалпы аффиндік коллектор ретінде қарастырылады қисық аффиналық кеңістіктің тегіс модель геометриясының деформациясы.
Аффин кеңістігі жазық модель геометриясы ретінде
Аффиналық кеңістіктің анықтамасы
Бейресми түрде, аффиналық кеңістік Бұл векторлық кеңістік таңдауынсыз шығу тегі. Ол геометриясын сипаттайды ұпай және тегін векторлар ғарышта. Түпнұсқаның болмауының нәтижесінде аффиналық кеңістіктегі нүктелерді біріктіруге болмайды, себебі векторлық қосу үшін параллелограмм заңын құратын шығу тегі таңдауды қажет етеді. Алайда, вектор v нүктеге қосылуы мүмкін б вектордың бастапқы нүктесін at орналастыру арқылы б содан кейін тасымалдау б терминалға дейін. Осылайша сипатталған операция б → б + v болып табылады аударма туралы б бойымен v. Техникалық тұрғыдан аффине n-кеңістік - жиынтық An жабдықталған өтпелі әрекет векторлық топ Rn осы тармақты аудару операциясы арқылы: An осылайша а негізгі біртекті кеңістік векторлық топ үшін Rn.
The жалпы сызықтық топ GL (n) болып табылады түрлендірулер тобы туралы Rn сақтайтын сызықтық құрылым туралы Rn деген мағынада Т(ав + bw) = aT(v) + bT(w). Ұқсастық бойынша аффиндік топ Афф (n) - түрлендірулер тобы An сақтау аффиналық құрылым. Осылайша φ ∈ афф (n) керек аудармаларды сақтау деген мағынада
қайда Т жалпы сызықтық түрлендіру болып табылады. Картаны жіберу φ ∈ афф (n) дейін Т L GL (n) Бұл топтық гомоморфизм. Оның ядро аудармалар тобы Rn. The тұрақтандырғыш кез келген нүкте б жылы A арқылы анықтауға болады GL (n) осы проекцияны қолдану: бұл аффиндік топты а ретінде жүзеге асырады жартылай бағыт өнім туралы GL (n) және Rn, және аффиндік кеңістік біртекті кеңістік Афф (n) / GL (n).
Аффиндік жақтаулар және жалпақ аффиндік байланыс
Ан аффиналық жақтау үшін A нүктеден тұрады б ∈ A және негіз (e1,… en) векторлық кеңістіктің ТбA = Rn. Жалпы сызықтық топ GL (n) түсірілім алаңында еркін әрекет етеді FA барлық аффиналық кадрларды бекіту арқылы б және негізді өзгерту (e1,… en) әдеттегідей және карта π аффиндік кадр жіберу (б; e1,… en) дейін б болып табылады квоталық карта. Осылайша FA Бұл негізгі GL (n)-бума аяқталды A. Әрекеті GL (n) табиғи түрде аффиндік топтың еркін өтпелі әрекетіне таралады Афф (n) қосулы FA, сондай-ақ FA болып табылады Афф (n)-торсор, және анықтамалық кадрды таңдау анықтайды FA → A негізгі байламмен Афф (n) → Афф (n) / GL (n).
Қосулы FA коллекциясы бар n + 1 функцияларымен анықталады
(бұрынғыдай) және
Үшін базалық нүктені таңдағаннан кейін A, мұның барлығы мәндері бар функциялар Rn, сондықтан оларды алуға болады сыртқы туындылар алу дифференциалдық 1-формалар мәндерімен Rn. Функциялардан бастап εмен үшін негіз беріңіз Rn әр нүктесінде FA, бұл 1-формалар форманың қосындылары ретінде көрінуі керек
кейбір коллекциялар үшін (θмен, ωк
j)1 ≤ мен, j, к ≤ n нақты бағаланатын бір формалардың Афф (n). Бұл негізгі пішіндегі бір пішінді жүйе FA → A аффиндік байланысты анықтайды A.
Сыртқы туындысын екінші рет қабылдау және сол фактіні қолдану г.2 = 0 сияқты сызықтық тәуелсіздік туралы εмен, келесі қатынастар алынады:
Бұл Маурер-Картан теңдеулері Өтірік тобы үшін Афф (n) (сәйкестендірілген FA анықтама шеңберін таңдау арқылы). Бұдан басқа:
- The Pfaffian жүйесі θj = 0 (барлығына j) болып табылады интегралды және оның интегралды коллекторлар негізгі байламның талшықтары болып табылады Афф (n) → A.
- Pfaffian жүйесі ωj
мен = 0 (барлығына мен, j) интегралданатын және оның интегралды коллекторлары параллель тасымалды анықтайды FA.
Осылайша формалар (ωj
мен) пәтерді анықтау негізгі байланыс қосулы FA → A.
Мотивациямен қатаң салыстыру үшін негізінен параллельді тасымалдауды анықтау керек Афф (n)-бума аяқталды A. Мұны істеуге болады артқа тарту FA тегіс карта бойынша φ : Rn × A → A аударма арқылы анықталады. Содан кейін композициялық φ. ∗ FA → FA → A негізгі болып табылады Афф (n)-бума аяқталды Aжәне нысандары (θмен, ωк
j) артқа тартыңыз тегіс негізгі қарыз беру Афф (n)- осы байламға қосу.
Жалпы аффиндік геометриялар: формальды анықтамалар
Аффинді кеңістік, кез-келген тегіс сияқты Клейн геометриясы, бұл тегіс Cartan қосылымымен жабдықталған коллектор. Жалпы аффиндік коллекторлар немесе аффиндік геометрияларды Маурер-Картан теңдеулерімен өрнектелген жазықтық шартын түсіру арқылы оңай алады. Анықтамаға жақындаудың бірнеше әдісі бар, екеуі беріледі. Екі анықтамаға да 1-форманы түсіну көмектеседі (θмен, ωк
j) жалған модельде Lie алгебрасындағы мәндері бар 1-пішінді беру үшін сәйкес келеді афф(n) аффиндік топтың Афф (n).
Осы анықтамаларда М тегіс n-көптік және A = Афф (n) / GL (n) бірдей өлшемдегі аффиналық кеңістік болып табылады.
Абсолютті параллелизм арқылы анықтама
Келіңіздер М көпжақты болу және P директор GL (n)-бума аяқталды М. Содан кейін аффиндік байланыс 1-форма болып табылады η қосулы P мәндерімен афф(n) келесі қасиеттерді қанағаттандыру
- η әрекетіне қатысты эквивариант болып табылады GL (n) қосулы P және афф(n);
- η(Xξ) = ξ барлығына ξ Ли алгебрасында gl(n) бәрінен де n × n матрицалар;
- η әрбір жанама кеңістігінің сызықтық изоморфизмі болып табылады P бірге афф(n).
Соңғы шарт осыны білдіреді η болып табылады абсолютті параллелизм қосулы Pяғни, ол тангенс байламын анықтайды P тривиальды байламмен (бұл жағдайда) P × афф(n)). Жұп (P, η) құрылымын анықтайды аффиндік геометрия қосулы М, оны аффиндік коллектор.
Аффин Ли алгебрасы афф(n) жартылай өнімі ретінде бөлінеді Rn және gl(n) солай η жұп түрінде жазылуы мүмкін (θ, ω) қайда θ мәндерді қабылдайды Rn және ω мәндерді қабылдайды gl(n). 1 және 2 шарттар тең ω директор болу GL (n)-қосылым және θ а-ны индукциялайтын көлденең эквивариант 1-форма бола отырып шумақ гомоморфизмі бастап ТМ дейін байланысты байлам P ×GL (n) Rn. 3-шарт осы шумақтың гомоморфизмінің изоморфизм екендігіне тең. (Алайда, бұл ыдырау аффиндік топтың ерекше құрылымының салдары болып табылады.) Бастап P болып табылады жақтау байламы туралы P ×GL (n) Rn, бұдан шығады θ арасындағы бума изоморфизмін қамтамасыз етеді P және жақтау байламы FМ туралы М; бұл аффиндік қосылыстың анықтаушы ретіндегі анықтамасын қалпына келтіреді GL (n)-қосылым қосулы FМ.
Жазық модельде пайда болатын 1-формалар тек компоненттер болып табылады θ және ω.
Анықтама негізгі аффиндік байланыс ретінде
Ан аффиндік байланыс қосулы М негізгі болып табылады Афф (n)-бума Q аяқталды М, директормен бірге GL (n)-бөлшек P туралы Q және директор Афф (n)-қосылу α (1-пішін қосулы Q мәндерімен афф(n)) келесілерді қанағаттандырады (жалпы) Картандық күй. The Rn кері тарту компоненті α дейін P көлденең эквивариант 1-форма болып табылады, сондықтан домалдың гомоморфизмін анықтайды ТМ дейін P ×GL (n) Rn: бұл изоморфизм болу үшін қажет.
Мотивациямен байланыс
Бастап Афф (n) әрекет етеді A, негізгі байламмен байланысты Q, байлам A = Q ×Афф (n) A, бұл талшықтың бумасы М оның талшығы х жылы М аффиндік кеңістік Aх. A бөлім а туралы A (белгіленген нүктені анықтау) ах жылы Aх әрқайсысы үшін х ∈ М) директорды анықтайды GL (n)-бөлшек P туралы Q (осы белгіленген нүктелердің тұрақтандырғыштарының шоғыры ретінде) және керісінше. Негізгі байланыс α анықтайды Эресманн байланысы осы байламда, демек, параллель тасымалдау ұғымы. Картан шарты ерекше бөлімді қамтамасыз етеді а әрқашан параллель тасымалдау кезінде қозғалады.
Қосымша қасиеттер
Қисықтық және бұралу
Қисықтық пен бұралу - аффиндік байланыстың негізгі инварианттары. Аффиналық байланыс ұғымын анықтайтын көптеген эквивалентті тәсілдер болғандықтан, қисықтық пен бұралуды анықтайтын көптеген түрлі әдістер бар.
Картандық байланыс тұрғысынан қисықтық аффиндік байланыстың сәтсіздігі болып табылады η Маурер-Картан теңдеуін қанағаттандыру үшін
мұндағы сол жақтағы екінші мүше сына өнімі пайдаланып Жалған жақша жылы афф(n) құндылықтармен келісім жасау. Кеңейту арқылы η жұпқа (θ, ω) және Ли алгебрасының құрылымын қолдану афф(n), бұл сол жағын екі формула бойынша кеңейтуге болады
мұнда сына өнімдері матрицалық көбейту арқылы бағаланады. Бірінші өрнек деп аталады бұралу байланыстың, ал екіншісі қисықтық деп те аталады.
Бұл өрнектер рамалық байламның жалпы кеңістігіндегі дифференциалды 2 пішінді. Алайда, олар көлденең және эквивариантты, демек тензорлық объектілерді анықтайды. Бұларды тікелей индукцияланған ковариант туындысынан анықтауға болады ∇ қосулы ТМ келесідей.
The бұралу формула бойынша берілген
Егер бұралу жоғалып кетсе, онда байланыс дейді бұралмалы емес немесе симметриялы.
Қисықтық формула бойынша берілген
Ескертіп қой [X, Y] болып табылады Векторлық өрістердің кронштейні
жылы Эйнштейн жазбасы. Бұл координаттар жүйесін таңдауға және
жанасу векторы б туралы менмың координаталық қисық. The ∂мен жанасу кеңістігінің табиғи негізі болып табылады б, және Xмен векторлық өрістің сәйкес координаттары X = Xмен ∂мен.
Қисықтық та, бұралу да жоғалған кезде, байланыс а анықтайды Лиге дейінгі алгебра тангенс байламының ғаламдық кесінділеріндегі құрылым.
Levi-Civita байланысы
Егер (М, ж) Бұл Риманн коллекторы онда ерекше аффиндік байланыс бар ∇ қосулы М келесі екі қасиетке ие:
- қосылыс бұралмалы емес, яғни Т∇ нөлге тең, сондықтан ∇XY - ∇YX = [X,Y];
- параллель тасымалдау - бұл изометрия, яғни ішкі өнімдер (қолдану арқылы анықталады) ж) жанама векторлар арасында сақталған.
Бұл байланыс деп аталады Levi-Civita байланысы.
«Симметриялық» термині көбінесе бірінші қасиет үшін бұралмалы емес орнына қолданылады. Екінші шарт байланыс а екенін білдіреді метрикалық байланыс Риман метрикасы деген мағынада ж параллель: ∇ж = 0. Бұралусыз байланыс үшін шарт сәйкестілікке тең X ж(Y, З) = ж (∇XY, З) +ж(Y,∇X З), «метрикамен үйлесімділік». [7] Жергілікті координаттарда форманың компоненттері деп аталады Christoffel рәміздері: Леви-Сивита байланысының бірегейлігіне байланысты бұл компоненттердің құрамдас бөліктері бойынша формуласы бар ж.
Геодезия
Түзу сызықтар аффиндік геометрияда түсінік болғандықтан, аффиндік байланыстар аффиндік геодезия деп аталатын кез-келген аффиндік коллектордағы (параметрленген) түзудің жалпыланған түсінігін анықтайды. Параметрлік қисық γ : Мен → М түзу сызық, егер оның жанасу векторы параллель болып қала берсе және бойымен тасымалданған кезде ол өзімен бірге теңдестірілген болса γ. Сызықтық тұрғыдан аффиндік байланыс М аффиндік геодезияны келесі жолмен ажыратады: тегіс қисық γ : Мен → М болып табылады аффиндік геодезиялық егер γ̇ параллель тасымалданады γ, Бұл
қайда τс
т : ТγсМ → ТγтМ - бұл қосылысты анықтайтын параллель көлік картасы.
Шексіз байланыс тұрғысынан ∇, осы теңдеудің туындысы көздейді
барлығына т ∈ Мен.
Керісінше, осы дифференциалдық теңдеудің кез-келген шешімі жанасу векторы қисық бойымен параллель тасымалданатын қисық береді. Әрқайсысы үшін х ∈ М және әрқайсысы X . ТхМ, бірегей аффинді геодезия бар γ : Мен → М бірге γ(0) = х және γ̇(0) = X және қайда Мен - ең үлкен ашық аралық R, құрамында геодезия анықталған 0 бар. Бұл Пикард - Линделёф теоремасы, және анықтауға мүмкіндік береді экспоненциалды карта аффиндік байланыспен байланысты.
Атап айтқанда, қашан М Бұл (жалған -)Риманн коллекторы және ∇ болып табылады Levi-Civita байланысы, онда аффиндік геодезия әдеттегідей геодезия Риман геометриясының қисықтары және жергілікті қашықтықты азайту қисықтары.
Мұнда анықталған геодезия кейде деп аталады аффинді түрде параметрленген, берілген түзу сызықтан бастап М параметрлік қисықты анықтайды γ сызық арқылы аффинді қайта параметризациялауға дейін γ(т) → γ(кезінде + б), қайда а және б тұрақты болып табылады. Аффиндік геодезияның жанама векторы параллель және өз бойында эквиполентті. Параметрленбеген геодезиялық немесе міндетті түрде эквилентті болмай, өз бойымен параллель болатын тек қана қанағаттандыруды қажет етеді
кейбір функциялар үшін к бірге анықталған γ. Параметрленбеген геодезия көбінесе көзқарас тұрғысынан зерттеледі проективті байланыстар.
Даму
Аффиндік байланыс деген ұғымды анықтайды даму қисықтар. Интуитивті түрде даму, егер деген түсінікке ие болса хт - қисық М, содан кейін аффиндік жанама кеңістік х0 мүмкін шиыршықталған қисық бойымен. Осылайша, жанасу кеңістігі мен коллектор арасындағы байланыс нүктесі қисық сызықты шығарады Cт осы аффиналық кеңістікте: хт.
Ресми түрде, рұқсат етіңіз τ0
т : ТхтМ → Тх0М аффиндік байланыспен байланысты сызықтық параллельді тасымалдау картасы болыңыз. Содан кейін даму Cт ішіндегі қисық Тх0М 0-ден басталады және жанамасына параллель болады хт барлық уақытта т:
Соның ішінде, хт Бұл геодезиялық егер оның дамуы аффиналық параметрленген түзу болса ғана Тх0М.[8]
Беттік теория қайта қаралды
Егер М - бұл бет R3, мұны байқау қиын емес М табиғи аффиндік байланысы бар. Сызықтық байланыс тұрғысынан векторлық өрістің ковариантты туындысы векторлық өрісті дифференциалдау арқылы анықталады, карта ретінде қарастырылады М дейін R3, содан кейін нәтижені ортадан горизонталь кеңістіктерге проекциялау М. Бұл аффиндік байланыстың бұралмалы емес екенін байқау қиын емес. Сонымен қатар, бұл Риман метрикасына қатысты метрикалық байланыс М ішкі өніммен индукцияланған R3, демек, бұл осы көрсеткіштің Леви-Сивита байланысы.
Мысал: Евклид кеңістігіндегі бірлік сфера
Келіңіздер ⟨ , ⟩ әдеттегідей болу скалярлы өнім қосулы R3және рұқсат етіңіз S2 өлшем бірлігі. Тангенс кеңістігі S2 бір сәтте х векторлық ішкі кеңістікпен табиғи түрде анықталады R3 ортогональды векторларынан тұрады х. Бұдан векторлық өріс шығады Y қосулы S2 карта ретінде қарастыруға болады Y : S2 → R3 бұл қанағаттандырады
Ретінде белгілеңіз г.Y осындай картаның дифференциалды (Якоб матрицасы). Сонда бізде:
- Лемма. Формула
- аффиндік байланысты анықтайды S2 жоғалып бара жатқан бұралумен.
- Дәлел. Мұны дәлелдеуге тура келеді ∇ лейбництік сәйкестікті қанағаттандырады және болып табылады C∞(S2) бірінші айнымалыдағы сызықтық. Демек, мұнда дәлелденуі керек нәрсе - жоғарыдағы карта шынымен жанама векторлық өрісті анықтайды. Яғни, мұны бәрімізге дәлелдеуіміз керек х жылы S2
- Дәлел. Мұны дәлелдеуге тура келеді ∇ лейбництік сәйкестікті қанағаттандырады және болып табылады C∞(S2) бірінші айнымалыдағы сызықтық. Демек, мұнда дәлелденуі керек нәрсе - жоғарыдағы карта шынымен жанама векторлық өрісті анықтайды. Яғни, мұны бәрімізге дәлелдеуіміз керек х жылы S2
- Картаны қарастырыңыз
- Картаны қарастырыңыз
- Карта f тұрақты, демек, оның дифференциалды мәні жоғалады. Соның ішінде
- Карта f тұрақты, демек, оның дифференциалды мәні жоғалады. Соның ішінде
- Жоғарыдағы 1-теңдеу келтірілген. Q.E.D.
Сондай-ақ қараңыз
- Атлас (топология)
- Байланыс (математика)
- Қосылу (талшықты коллектор)
- Қосылу (аффинді шоқ)
- Дифференциалданатын коллектор
- Дифференциалды геометрия
- Жалпы салыстырмалылық математикасына кіріспе
- Levi-Civita байланысы
- Риман геометриясындағы формулалар тізімі
- Риман геометриясы
Ескертулер
- ^ Нәтижесінде көптеген математиктер бұл терминді қолданады сызықтық байланыс (орнына аффиндік байланыс) жанасатын байламдағы байланыс үшін, негіздеме бойынша параллель тасымалдау сызықты және аффинді емес. Алайда, кез-келген үшін бірдей қасиет бар (Koszul немесе сызықтық Эресманн) векторлық байламдағы байланыс. Бастапқыда термин аффиндік байланыс аффине үшін қысқа байланыс Картан мағынасында және бұл байланыс ерікті векторлық байламнан гөрі, жанама байламда анықталғанын білдіреді. Сызықтық картандық байланыс ұғымы шынымен де мағынасы жоқ, өйткені сызықтық көріністер өтпелі емес.
- ^ Картанның интуициясын шақырусыз нақты ету қиын тегіс шексіз талдау, бірақ бір тәсілі - оның ойларын ескеру айнымалы, бұл кейбір көрінбейтін параметрлер кеңістігінен кейін ажыратуға болатын коллекторға түсетін карталар.
- ^ Классикалық түрде жанасу кеңістігі шексіз жуықтау ретінде қарастырылды, ал қазіргі дифференциалдық геометрияда жанамалық кеңістіктер көбінесе туындылар сияқты дифференциалды нысандармен анықталады.[4]
- ^ Мұны шығу тегі ретінде қарастыруға болады: шын мәнінде тек жағдайды қарастыру жеткілікті б = ах; Картан мұны жанама түрде анықтайды х жылы М.
Әдебиеттер тізімі
- ^ Вейл 1918, 1922 жылға дейінгі 5 басылым.
- ^ Картан 1923 ж.
- ^ Картан 1926.
- ^ Кобаяши және Номизу 1996 ж, 1 том, 1.1-1.2 бөлімдері
- ^ Толығырақ ақпаратты қараңыз Ü. Lumiste (2001б). Келесі интуитивті емдеу әдісі Картан (1923) және Картан (1926).
- ^ Cf. Р. Герман (1983), 1-3 қосымшалар Картан (1951), және Шарп (1997).
- ^ Кобаяши және Номизу 1996 ж, б. 160, т. Мен
- ^ Дамудың бұл әдісі Кобаяши және Номизу (1996, 1 том, III.3.1 ұсыныс); Неғұрлым геометриялық өңдеу үшін III.3 бөлімін қараңыз. Сондай-ақ қараңыз Шарп (1997) басқа геометриялық жағдайларда дамуды мұқият талқылау үшін.
Бастапқы тарихи сілтемелер
- Кристоффель, Элвин Бруно (1869), «Über die Transformation der homogenen Differentialausdrücke zweiten сыныптары», Mathematik журналы жазылады, 1869 (70): 46–70, дои:10.1515 / crll.1869.70.46
- Леви-Сивита, Туллио (1917), «Nozione di parallelismo in una varietà qualunque e conseguente specificazione geometrica della curvatura Riemanniana», Көрсету. Шеңбер Мат Палермо, 42: 173–205, дои:10.1007 / bf03014898
- Картан, Эли (1923), «Sur les variétés à connexion affine, et la théorie de la relativité généralisée (première partie)», Annales Scientifiques de l'École Normale Supérieure, 40: 325–412, дои:10.24033 / asens.751
- Картан, Эли (1924), "Sur les variétés à connexion affine, et la théorie de la relativité généralisée (première partie) (Suite)", Annales Scientifiques de l'École Normale Supérieure, 41: 1–25, дои:10.24033 / asens.753
- Cartan, Élie (1986), On Manifolds with Affine Connection and the Theory of General Relativity, Humanities Press
- Cartan's treatment of affine connections as motivated by the study of relativity theory. Includes a detailed discussion of the physics of reference frames, and how the connection reflects the physical notion of transport along a worldline.
- Cartan, Élie (1926), "Espaces à connexion affine, projective et conforme", Acta Math., 48: 1–42, дои:10.1007 / BF02629755
- A more mathematically motivated account of affine connections.
- Cartan, Élie (1951), Роберт Германның қосымшаларымен (ред.), Риман кеңістігінің геометриясы (Джеймс Глэйзбрук аударған Leçons sur la géométrie des espaces de Riemann, 2-ші басылым), Math Sci Press, Массачусетс (1983 ж. Жарияланған), ISBN 978-0-915692-34-7.
- Affine connections from the point of view of Риман геометриясы. Robert Hermann's appendices discuss the motivation from surface theory, as well as the notion of affine connections in the modern sense of Koszul. He develops the basic properties of the differential operator ∇, and relates them to the classical affine connections in the sense of Cartan.
- Вейл, Герман (1918), Raum, Zeit, Materie (5 editions to 1922, with notes by Jürgen Ehlers (1980), translated 4th edition Space, Time, Matter by Henry Brose, 1922 (Methuen, reprinted 1952 by Dover) ed.), Springer, Berlin, ISBN 0-486-60267-2
Екінші сілтемелер
- Кобаяши, Шошичи; Nomizu, Katsumi (1996), Foundations of Differential Geometry, Vols. 1 және 2 (Жаңа ред.), Вили-Интерсианс, ISBN 0-471-15733-3.
- This is the main reference for the technical details of the article. Volume 1, chapter III gives a detailed account of affine connections from the perspective of principal bundles on a manifold, parallel transport, development, geodesics, and associated differential operators. Volume 1 chapter VI gives an account of affine transformations, torsion, and the general theory of affine geodesy. Volume 2 gives a number of applications of affine connections to біртекті кеңістіктер және күрделі коллекторлар, as well as to other assorted topics.
- Lumiste, Ülo (2001a), «Аффиндік байланыс», жылы Хазевинкель, Мичиел (ред.), Математика энциклопедиясы, Kluwer Academic Publishers, ISBN 978-1-55608-010-4.
- Lumiste, Ülo (2001b), «Коллектордағы қосылыстар», жылы Хазевинкель, Мичиел (ред.), Математика энциклопедиясы, Kluwer Academic Publishers, ISBN 978-1-55608-010-4.
- Two articles by Lumiste, giving precise conditions on parallel transport maps in order that they define affine connections. They also treat curvature, torsion, and other standard topics from a classical (non-principal bundle) perspective.
- Sharpe, R.W. (1997), Дифференциалдық геометрия: Клейннің Эрланген бағдарламасын картаның жалпылауы, Springer-Verlag, Нью-Йорк, ISBN 0-387-94732-9.
- This fills in some of the historical details, and provides a more reader-friendly elementary account of Cartan connections in general. Appendix A elucidates the relationship between the principal connection and absolute parallelism viewpoints. Appendix B bridges the gap between the classical "rolling" model of affine connections, and the modern one based on principal bundles and differential operators.











![{ displaystyle mathrm {d} eta + { tfrac {1} {2}} [ eta wedge eta] = 0,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d3c2e421eebf09b6ad8f285b378bd806fda66004)

![T ^ { nabla} (X, Y) = nabla _ {X} Y- nabla _ {Y} X- [X, Y].](https://wikimedia.org/api/rest_v1/media/math/render/svg/4f19951452740bcb62cd949121b3571e305b0ddd)
![R _ {{X, Y}} ^ { nabla} Z = nabla _ {X} nabla _ {Y} Z- nabla _ {Y} nabla _ {X} Z- nabla _ {{[X , Y]}} Z.](https://wikimedia.org/api/rest_v1/media/math/render/svg/0dbbbbf6baa6b3bd6432093e89b2be32f36df9a2)
![{ displaystyle [X, Y] = сол жақ (X ^ {j} ішінара _ {j} Y ^ {i} -Y ^ {j} жартылай _ {j} X ^ {i} оң) жартылай _ {i}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/40689fe0b2339f0df9519e0138de4681fb36a29e)









