Кватернион - Quaternion

Көбейту циклдарын көрсететін Cayley Q8 графигі мен, j және к – жылы SVG файлы, оны бөлектеу үшін циклді апарыңыз немесе нұқыңыз

Жылы математика, кватерниондар болып табылады санау жүйесі кеңейтетін күрделі сандар. Оларды алғаш ирландиялық математик суреттеген Уильям Роуэн Гамильтон 1843 жылы^[1][2] және қолданылды механика жылы үш өлшемді кеңістік. Кватерниондардың ерекшелігі - екі кватернионды көбейту коммутативті емес. Гамильтон кватернионды квитент үш өлшемді кеңістікте бағытталған екі сызықтың^[3] немесе екеуінің эквиваленті ретінде векторлар.^[4]

Төрттіктер негізінен келесі түрде ұсынылады:

${ displaystyle a + b mathbf {i} + c mathbf {j} + d mathbf {k}}$

қайда а, б, c, және г. нақты сандар және мен, j, және к негізгі болып табылады кватернион бірліктері.

Quaternions жылы қолданылады таза математика, және де практикалық қолданыста болады қолданбалы математика - атап айтқанда үш өлшемді айналуларға қатысты есептеулер сияқты көлемді компьютерлік графика, компьютерлік көру, және кристаллографиялық құрылым талдау.^[5] Тәжірибелік қолданбаларда оларды басқа әдістермен қатар қолдануға болады, мысалы Эйлер бұрыштары және айналу матрицалары, немесе қолданылуына байланысты оларға балама ретінде.

Қазіргі математикалық тілде кватериондар төрт-өлшемді ассоциативті алгебра үстінен нақты сандар, демек, а домен. Іс жүзінде кватериондар бірінші болды алгебра ашылуы керек. Кватерниондар алгебрасын көбінесе белгілейді H (үшін Гамильтон), немесе қара тақта арқылы ${ displaystyle mathbb {H}}$ (Юникод U + 210D, ℍ). Ол сондай-ақ Клиффорд алгебрасы жіктемелер Cl_0,2(ℝ) ≅ Cl⁺
_3,0(ℝ). Алгебра ℍ сәйкес, талдауда ерекше орын алады Фробениус теоремасы, бұл тек ақырлы өлшемді екінің бірі бөлу сақиналары құрамында нақты сандар жеке тұлға ретінде қосылу, екіншісі - күрделі сандар. Бұл сақиналар да Евклидтік Хурвиц алгебралары, оның ішінде кватерниондар ең үлкені ассоциативті алгебра. Кватерниондарды одан әрі кеңейту нәтижесінде ассоциативті емес октониондар, бұл соңғы алгебра реал үстінде (октониялардың кеңеюі, седенциялар, бар нөлдік бөлгіштер және сондықтан алгебра нормаланған бөліну бола алмайды).^[6]

The кватерниондар бойынша топтық құрылымды таңдау ретінде қарастыруға болады 3-сфера S³ бұл топқа мүмкіндік береді Айналдыру (3) изоморфты болып табылады СУ (2) және сонымен бірге әмбебап қақпақ туралы Ж (3).

Кватернион қондырғыларының өнімін графиктік бейнелеу, 4D-кеңістіктегі жазықтықта 90 ° - айналу, екіге созылған {1, мен, j, к}. Сол жақ коэффициентті оңға қарай бұруға болады. Мысалға:
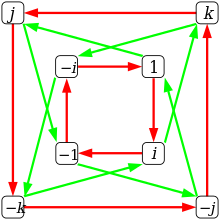
көк түспен: 1 /мен-планет: 1 ⋅мен = мен, мен/к-планет: мен ⋅ j = к
жылы қызыл: 1/j-планет: 1 ⋅j = j, j/к-планет: j ⋅ мен = -к

Тарих

Кватернион тақтасы қосулы Brougham (сыпырғыш) көпірі, Дублин, онда:

Міне, ол өтіп бара жатып
16 қазан 1843 ж
Сэр Уильям Роуэн Гамильтон
ашылған данышпанның жарқылында
үшін негізгі формула
кватернионды көбейту
мен² = j² = к² = i j k = −1
& оны осы көпірдің тасына кесіп таста

Кватерниондарды Гамильтон 1843 ж. Енгізген.^[7] Бұл жұмыстың маңызды прекурсорлары қамтылған Эйлердің төрт квадраттық сәйкестігі (1748) және Олинде Родригес ' жалпы айналулардың төрт параметр бойынша параметрленуі (1840), бірақ бұл жазушылардың ешқайсысы төрт параметрді айналдыруды алгебра ретінде қарастырмады.^[8][9] Карл Фридрих Гаусс 1819 жылы кватерниондар ашқан, бірақ бұл жұмыс 1900 жылға дейін жарық көрген жоқ.^[10][11]

Гамильтон бұл туралы білді күрделі сандар деп түсіндіруге болатын еді ұпай ішінде ұшақ және ол үшөлшемді нүктелер үшін дәл осылай жасаудың жолын іздеді ғарыш. Кеңістіктегі нүктелерді олардың координаттарымен көрсетуге болады, олар сандардың үштіктері болып табылады және көптеген жылдар бойы ол сандардың үштіктерін қосу және азайтуды білген. Алайда, Гамильтон көбейту және бөлу мәселесімен ұзақ уақыт бойы айналысты. Ол қалай есептеуге болатындығын біле алмады квитент кеңістіктегі екі нүктенің координаталарының. Шынында, Фердинанд Георг Фробениус кейінірек дәлелденді 1877 жылы бұл а алгебра бөлімі ақырлы және ассоциативті болатын нақты сандардың үстінде ол үшөлшемді бола алмайды және мұндай алгебралардың тек үшеуі бар: сәйкесінше 1, 2 және 4 өлшемдері бар ℝ, ℂ (күрделі сан) және ℍ (кватернион). .

Кватерниондардағы үлкен жетістік 1843 жылы 16 қазанда дүйсенбіде келді Дублин, Гамильтон бара жатқанда Ирландия корольдік академиясы ол кеңес мәжілісінде қайда төрағалық етпек болды. Ол жүріс жолымен жүріп өтті Корольдік канал оның әйелімен бірге төрттік тұжырымдамалар оның санасында қалыптаса бастады. Жауап оған түскенде, Гамильтон кватерниондардың формуласын ойып алуға деген ұмтылысқа қарсы тұра алмады,

${ displaystyle mathbf {i} ^ {2} = mathbf {j} ^ {2} = mathbf {k} ^ {2} = mathbf {i , j , k} = -1}$

тасқа Brougham Bridge ол бұған тоқтап тұрды. Ою қашан жоғалып кеткенімен, 1989 жылдан бастап жыл сайынғы қажылық бар Гамильтон серуені бастап жүретін ғалымдар мен математиктер үшін Дунсинк обсерваториясы Гамильтонның ашылуын еске алу үшін Корольдік канал көпіріне.

Келесі күні Гамильтон өзінің досы және математик Джон Т.Грейвске хат жазып, оның ашылуына себеп болған ой пойызын сипаттады. Бұл хат кейінірек хатында жарияланды Лондон, Эдинбург және Дублин философиялық журналы және ғылым журналы;^[12] Гамильтон:

Міне, үш есе есептеу үшін кеңістіктің төртінші өлшемін қандай да бір мағынада қабылдауымыз керек деген түсінік пайда болды ... Электр тізбегі жабылып, ұшқын пайда болды.^[12]

Гамильтон төртеуді осы көбейту ережелерімен а деп атады кватернионжәне ол өмірінің қалған бөлігін оларды зерттеуге және оқытуға арнады. Гамильтонды емдеу көп геометриялық квартниондарды атап көрсететін заманауи тәсілге қарағанда алгебралық қасиеттері. Ол «кватернионистер» мектебін құрды және бірнеше кітаптарда кватерниондарды танымал етуге тырысты. Оның соңғы және ең ұзын кітаптары, Төрттік элементтер,^[13] 800 парақ болды; оны редакциялады оның ұлы және ол қайтыс болғаннан кейін көп ұзамай жарияланды.

Гамильтон қайтыс болғаннан кейін оның оқушысы Питер Тэйт квартниондарды насихаттауды жалғастырды. Осы кезде кватериондар Дублинде міндетті емтихан тақырыбы болды. Сияқты векторларды қолдана отырып сипатталатын физика мен геометрияның тақырыптары кинематика ғарышта және Максвелл теңдеулері, толығымен кватерниондар тұрғысынан сипатталған. Тіпті кәсіби зерттеу қауымдастығы болды Quaternion қоғамы, кватерниондарды зерттеуге арналған және т.б. гиперкомплекс саны жүйелер.

1880 жылдардың ортасынан бастап кватерниондар ығыстырыла бастады векторлық талдау әзірлеген болатын Джозия Уиллард Гиббс, Оливер Хивисайд, және Герман фон Гельмгольц. Векторлық талдаулар кватерниондар сияқты құбылыстарды сипаттады, сондықтан ол кейбір идеялар мен терминологияны кватерниондар туралы әдебиеттерден еркін алды. Алайда, векторлық талдау тұжырымдамалық тұрғыдан қарапайым және шартты түрде таза болды, нәтижесінде кватериондар кішігірім рөлге ауыстырылды математика және физика. Бұл ауысудың жанама әсері мынада Гамильтонның жұмысы көптеген заманауи оқырмандар үшін түсіну қиын. Гамильтонның бастапқы анықтамалары таныс емес, оның жазу стилі сөзге жақын және оны орындау қиын болды.

Алайда, кватерниондар 20 ғасырдың аяғынан бастап қайта жандана бастады, ең алдымен олардың пайдалылығына байланысты кеңістіктегі айналуларды сипаттайтын. Кватерниондар бойынша айналу кескіндері матрицалармен салыстырғанда ықшам және жылдам есептеледі. Сонымен қатар, айырмашылығы Эйлер бұрыштары, олар «сезімтал емесгимбалды құлып ». Осы себептен кватериондар қолданылады компьютерлік графика,^[14][15] компьютерлік көру, робототехника,^[16] басқару теориясы, сигналдарды өңдеу, қатынасты бақылау, физика, биоинформатика,^[17][18] молекулалық динамика, компьютерлік модельдеу, және орбиталық механика. Мысалы, бұл жиі кездеседі қатынасты бақылау кватерниондар бойынша басқарылатын ғарыш аппараттарының жүйелері. Кватерниондар тағы бір серпіліс алды сандар теориясы байланыстарына байланысты квадраттық формалар.^[19]

Физикадағы кватерниондар

П.Р.Джирардтың 1984 жылғы эссесі Кватернион тобы және қазіргі физика^[20] кватерниондардың физикадағы кейбір рөлдерін талқылайды. Эссе физикалық ковариацияның әр түрлі топтарын, атап айтқанда Ж (3), Лоренц тобы, салыстырмалық топтың жалпы теориясы, Клиффорд алгебрасы СУ (2) және конформды топ, оңай байланысты болуы мүмкін кватернион тобы жылы қазіргі алгебра. Джирард пікірталастардан бастады топтық өкілдіктер және кейбіреулерін ұсыну арқылы ғарыштық топтар туралы кристаллография. Ол жалғастырды кинематика туралы қатты дене қозғалыс. Содан кейін ол күрделі кватериондарды қолданды (бикватерниондар ) үшін Лоренц тобы ерекше салыстырмалылық, оның ішінде Томас прецессия. Деп бастап бес авторды келтірді Людвик Сильберштейн, кім қолданды потенциал біреуінің функциясы кватернион айнымалысы білдіру Максвелл теңдеулері жалғыз дифференциалдық теңдеу. Жалпы салыстырмалылыққа қатысты ол: Рунге - Ленц векторы. Ол Клиффорд бикватерниондары туралы айтты (бөлінген бикватерниондар ) данасы ретінде Клиффорд алгебрасы. Соңында, бикватернионның өзара әрекетін қолдана отырып, Джирар сипаттады конформды карталар қосулы ғарыш уақыты. Елу сілтемелердің қатарына Джирард кірді Александр Макфарлейн және оның Хабаршы туралы Quaternion қоғамы. 1999 жылы ол Эйнштейннің жалпы салыстырмалық теңдеулерін квартниондармен тікелей байланысты Клиффорд алгебрасында қалай тұжырымдалатынын көрсетті.^[21]

1924 ж кванттық механика The айналдыру электрон және басқа зат бөлшектерінің (белгілі шпинаторлар ) олардың қызығушылығын арттырған кватериондардың көмегімен сипаттауға болады; кватерниондар электрондардың 360 ° айналуын 720 ° -тан қалай ажыратуға болатындығын түсінуге көмектесті («Пластиналық трюк ”).^[22][23] 2018 жылғы жағдай бойынша^{[жаңарту]}, олардың қолданылуы қуып жеткен жоқ айналу топтары.^[a]

Анықтама

A кватернион болып табылады өрнек форманың

${ displaystyle a + b , mathbf {i} + c , mathbf {j} + d , mathbf {k} ,}$

қайда а, б, c, г., болып табылады нақты сандар, және мен, j, к, болып табылады шартты белгілер бұл үш кеңістіктік осьтің бойымен бағытталған бірлік-векторлар ретінде түсіндірілуі мүмкін. Іс жүзінде, егер біреуі а, б, c, г. 0-ге тең, тиісті термин алынып тасталады; егер а, б, c, г. барлығы нөлге тең, кватернион - нөлдік кватернион, 0 деп белгіленді; егер біреуі б, c, г. 1-ге тең, сәйкес термин жай жазылады мен, j, немесе к.

Гамильтон кватернионды сипаттайды ${ displaystyle q = a + b , mathbf {i} + c , mathbf {j} + d , mathbf {k}}$, а-дан тұратын сияқты скаляр бөлігі және векторлық бөлігі. Кватернион ${ displaystyle b , mathbf {i} + c , mathbf {j} + d , mathbf {k}}$ деп аталады векторлық бөлік (кейде ойдан шығарылған бөлік) of q, және а болып табылады скалярлық бөлік (кейде нақты бөлігі) of q. Оның нақты бөлігіне тең кватерион (яғни оның векторлық бөлігі нөлге тең) а деп аталады скаляр немесе нағыз кватернион, және сәйкес нақты санмен анықталады. Яғни, нақты сандар ендірілген төрттіктерде. (Дәлірек айтқанда, нақты сандардың өрісі кватерниондардың ішкі жиынына изоморфты. Күрделі сандардың өрісі кватерниондардың үш жиынына изоморфты.)^[24] Оның векторлық бөлігіне тең болатын кватернион а деп аталады векторлық кватернион.

Кватерниондар жиынтығы 4 өлшемді болып келеді векторлық кеңістік нақты сандардың үстінен, ${ displaystyle left {, 1, mathbf {i}, mathbf {j}, mathbf {k} , right }}$ сияқты негіз, компоненттік қосу арқылы

${ displaystyle (a_ {1} + b_ {1} , mathbf {i} + c_ {1} , mathbf {j} + d_ {1} , mathbf {k}) + (a_ {2 } + b_ {2} , mathbf {i} + c_ {2} , mathbf {j} + d_ {2} , mathbf {k}) = (a_ {1} + a_ {2}) + (b_ {1} + b_ {2}) , mathbf {i} + (c_ {1} + c_ {2}) , mathbf {j} + (d_ {1} + d_ {2}) , mathbf {k} ,,}$

және компоненттік скалярлық көбейту

${ displaystyle lambda (a + b , mathbf {i} + c , mathbf {j} + d , mathbf {k}) = lambda a + ( lambda b) , mathbf {i } + ( lambda c) , mathbf {j} + ( lambda d) , mathbf {k}.}$

Деп аталатын мультипликативті топтық құрылым Гамильтон өнімі, қатар қою арқылы белгіленетін кватериондарда келесі жолмен анықтауға болады:

• Нағыз кватернион 1 болып табылады сәйкестендіру элементі.
• The нақты кватерниондар барлық басқа кватерниондармен жүреді, яғни ақ = qa әрбір кватернион үшін q және әрбір нақты кватерион а. Алгебралық терминологияда бұл нақты кватериондар өрісі болып табылады орталығы осы кватернион алгебрасы.
• Өнім алдымен базалық элементтерге беріледі (келесі ішкі бөлімді қараңыз), содан кейін барлық кватерниондарға үлестіруші мүлік және нақты кватериондардың орталық қасиеті. Гамильтон өнімі ондай емес ауыстырмалы, бірақ ассоциативті, осылайша кватерниондар ан ассоциативті алгебра шындықтың үстінде.
• Сонымен қатар, нөлдік емес кез-келген кватернионның Гамильтон өніміне кері қатынасы бар:

${ displaystyle (a + b , mathbf {i} + c , mathbf {j} + d , mathbf {k}) ^ {- 1} = { frac {1} {a ^ {2 } + b ^ {2} + c ^ {2} + d ^ {2}}} , (ab , mathbf {i} -c , mathbf {j} -d , mathbf {k} ).}$

Осылайша кватерниондар а алгебра бөлімі.

Негіздік элементтерді көбейту

Негізгі элементтер мен, j, және к нақты кватерионмен жүру 1, яғни

${ displaystyle mathbf {i} cdot 1 = 1 cdot mathbf {i} = mathbf {i}, qquad mathbf {j} cdot 1 = 1 cdot mathbf {j} = mathbf { j}, qquad mathbf {k} cdot 1 = 1 cdot mathbf {k} = mathbf {k} ,.}$

Негізгі элементтердің басқа өнімдері анықталады

${ displaystyle mathbf {i} ^ {2} = mathbf {j} ^ {2} = mathbf {k} ^ {2} = - 1 ,,}$

және

${ displaystyle { begin {alignedat} {2} mathbf {ij} & = mathbf {k} ,, & qquad mathbf {ji} & = - mathbf {k} ,, mathbf {jk} & = mathbf {i} ,, & mathbf {kj} & = - mathbf {i} ,, mathbf {ki} & = mathbf {j} ,, & mathbf {ik} & = - mathbf {j} ,. end {alignedat}}}$

Бұл көбейту формулалары барабар

${ displaystyle mathbf {i} ^ {2} = mathbf {j} ^ {2} = mathbf {k} ^ {2} = mathbf {ijk} = -1 ~.}$

Шындығында, теңдік ijk = –1 нәтижелері

${ displaystyle ( mathbf {ij}) mathbf {k} = mathbf {k} ^ {2} = - 1.}$

Керісінше манипуляциялар келесіге ұқсас манипуляциялардан туындайды. Екі жағын да оңға көбейту арқылы −1 = ijk арқылы –к, біреу алады

${ displaystyle mathbf {k} = ( mathbf {ijk}) (- mathbf {k}) = ( mathbf {ij}) (- mathbf {k} ^ {2}) = mathbf {ij} ,.}$

Барлық басқа өнімдерді ұқсас әдістермен анықтауға болады.

Орталық

The орталығы а коммутативті емес сақина элементтердің қосалқы жазбасы болып табылады c осындай cx = xc әрқайсысы үшін х. Кватернион алгебрасының орталығы - нақты кватерниондардың кіші алаңы. Шын мәнінде, бұл нақты кватерниондардың орталыққа жататындығы туралы анықтаманың бөлігі. Керісінше, егер q = а + б мен + c j + г. к сол кезде орталыққа жатады

${ displaystyle 0 = mathbf {i} , qq , mathbf {i} = 2c , mathbf {ij} + 2d , mathbf {ik} = 2c , mathbf {k} -2d , mathbf {j} ,,}$

және c = г. = 0. Ұқсас есептеу j орнына мен біреуінде де бар екенін көрсетеді б = 0. Осылайша q = а Бұл нақты кватернион.

Төрттіктер а алгебра бөлімі. Бұл көбейтудің коммутативтілігі емес, кватерниондарды а-дан ерекшелейтін жалғыз қасиет екенін білдіреді өріс. Коммутативтіліктің күтпеген салдары бар, олардың арасында а көпмүшелік теңдеу төрттіктердің үстінде көпмүшелік дәрежесіне қарағанда айқын шешімдер болуы мүмкін. Мысалы, теңдеу з² + 1 = 0, кватерниондар болатын шексіз көп кватернион ерітінділеріне ие з = б мен + c j + г. к осындай б² + c² + г.² = 1. Осылайша, «-1» түбірлері а құрайды бірлік сферасы векторлық кватерниондардың үш өлшемді кеңістігінде.

Гамильтон өнімі

Екі элемент үшін а₁ + б₁мен + c₁j + г.₁к және а₂ + б₂мен + c₂j + г.₂к, деп аталатын олардың өнімі Гамильтон өнімі (а₁ + б₁мен + c₁j + г.₁к) (а₂ + б₂мен + c₂j + г.₂к), негіз элементтерінің туындыларымен анықталады және тарату құқығы. Дистрибьюторлық заң өнімді негізгі элементтердің жиынтығы болатындай етіп кеңейтуге мүмкіндік береді. Бұл келесі өрнекті береді:

${ displaystyle { begin {alignedat} {4} & a_ {1} a_ {2} && + a_ {1} b_ {2} mathbf {i} && + a_ {1} c_ {2} mathbf {j} && + a_ {1} d_ {2} mathbf {k} {} + {} & b_ {1} a_ {2} mathbf {i} && + b_ {1} b_ {2} mathbf {i} ^ {2} && + b_ {1} c_ {2} mathbf {ij} && + b_ {1} d_ {2} mathbf {ik} {} + {} & c_ {1} a_ {2} mathbf {j} && + c_ {1} b_ {2} mathbf {ji} && + c_ {1} c_ {2} mathbf {j} ^ {2} && + c_ {1} d_ {2} mathbf {jk} {} + {} & d_ {1} a_ {2} mathbf {k} && + d_ {1} b_ {2} mathbf {ki} && + d_ {1} c_ {2} mathbf {kj} && + d_ {1} d_ {2} mathbf {k} ^ {2} end {alignedat}}}$

Енді базалық элементтерді жоғарыда келтірілген ережелер арқылы көбейтуге болады:^[7]

${ displaystyle { begin {alignedat} {4} & a_ {1} a_ {2} && - b_ {1} b_ {2} && - c_ {1} c_ {2} && - d_ {1} d_ {2} {} + {} (& a_ {1} b_ {2} && + b_ {1} a_ {2} && + c_ {1} d_ {2} && - d_ {1} c_ {2}) mathbf { i} {} + {} (& a_ {1} c_ {2} && - b_ {1} d_ {2} && + c_ {1} a_ {2} && + d_ {1} b_ {2}) mathbf {j} {} + {} (& a_ {1} d_ {2} && + b_ {1} c_ {2} && - c_ {1} b_ {2} && + d_ {1} a_ {2} ) mathbf {k} end {alignedat}}}$

Екі өнімі айналмалы кватерниондар^[25] айналуға тең болады а₂ + б₂мен + c₂j + г.₂к содан кейін айналу а₁ + б₁мен + c₁j + г.₁к.

Скалярлық және векторлық бөліктер

Пішіннің кватернионы а + 0 мен + 0 j + 0 к, қайда а нақты сан болып табылады, деп аталады скаляр, және форманың кватерионы 0 + б мен + c j + г. к, қайда б, c, және г. нақты сандар, және олардың кем дегенде біреуі б, c немесе г. нөлге тең емес, а деп аталады векторлық кватернион. Егер а + б мен + c j + г. к кез-келген кватернион а оның деп аталады скалярлық бөлік және б мен + c j + г. к оның деп аталады векторлық бөлік. Әрбір кватернионды төртөлшемді векторлық кеңістіктегі вектор ретінде қарастыруға болатындығына қарамастан, вектор үш өлшемді кеңістіктегі векторлар ретінде. Бұл шартпен вектор векторлық кеңістіктің элементімен бірдей ℝ³.^[b]

Гамильтон векторлық кватерниондарды да атады оң жақ кватерниондар^[27][28] және нақты сандар (векторлық бөлігі нөлге тең квартниондар ретінде қарастырылады) скаляр кватерниондар.

Егер кватернион скалярлық бөлікке және векторлық бөлікке бөлінсе, яғни.

${ displaystyle mathbf {q} = (r, { vec {v}}), ~~ mathbf {q} in mathbb {H}, ~~ r in mathbb {R}, ~~ { vec {v}} in mathbb {R} ^ {3}}$

онда қосу мен көбейту формулалары:

${ displaystyle (r_ {1}, { vec {v}} _ {1}) + (r_ {2}, { vec {v}} _ {2}) = (r_ {1} + r_ {2}, { vec {v}} _ {1} + { vec {v}} _ {2})}$

${ displaystyle (r_ {1}, { vec {v}} _ {1}) (r_ {2}, { vec {v}} _ {2}) = (r_ {1} r_ {2 } - { vec {v}} _ {1} cdot { vec {v}} _ {2}, r_ {1} { vec {v}} _ {2} + r_ {2} { vec {v}} _ {1} + { vec {v}} _ {1} times { vec {v}} _ {2})}$

қайда «·«бұл нүктелік өнім және »×«бұл кросс өнім.

Конъюгация, норма және өзара

Кватерниондардың конъюгациясы күрделі сандардың конъюгациясы мен элементтердің транспозициясына (кері айналу деп те аталады) ұқсас. Клиффорд алгебралары. Оны анықтау үшін рұқсат етіңіз ${ displaystyle q = a + b , mathbf {i} + c , mathbf {j} + d , mathbf {k}}$ кватернион бол. The конъюгат туралы q кватернион ${ displaystyle q ^ {*} = a-b , mathbf {i} -c , mathbf {j} -d , mathbf {k}}$. Ол арқылы белгіленеді q^∗, q^т, ${ displaystyle { tilde {q}}}$, немесе q.^[7] Біріктіру - бұл инволюция, бұл оның өзіндік кері екенін білдіреді, сондықтан элементті екі рет конъюгациялау бастапқы элементті қайтарады. Екі кватернион көбейтіндісінің конъюгаты - конъюгаттардың туындысы кері тәртіпте. Яғни, егер б және q квартниондар (pq)^∗ = q^∗б^∗, емес б^∗q^∗.

Кватернионның конъюгациясы, күрделі жағдайдан түбегейлі айырмашылығы, кватерниондарды көбейту және қосу арқылы көрсетілуі мүмкін:

${ displaystyle q ^ {*} = - { frac {1} {2}} (q + , mathbf {i} , q , mathbf {i} + , mathbf {j} , q , mathbf {j} + , mathbf {k} , q , mathbf {k}) ~.}$

Конъюгацияны кватернионның скалярлық және векторлық бөліктерін бөліп алуға болады. Скаляр бөлігі б болып табылады 1/2(б + б^∗) , және векторлық бөлігі б болып табылады 1/2(б − б^∗) .

Кватернион көбейтіндісінің квадрат түбірін оның конъюгаты бар деп атайды норма және белгіленеді ||q|| (Гамильтон бұл шама деп атады тензор туралы q, бірақ бұл қазіргі заманғы мағынасына қайшы келеді »тензор Формулада бұл келесідей көрінеді:

${ displaystyle lVert q rVert = { sqrt {, qq ^ {*} ~}} = { sqrt {, q ^ {*} q ~}} = { sqrt {, a ^ {2 } + b ^ {2} + c ^ {2} + d ^ {2} ~}}}$

Бұл әрқашан теріс емес нақты сан, және ол Евклидтің нормасымен бірдей ℍ векторлық кеңістік ретінде қарастырылады ℝ⁴. Кватернионды нақты санға көбейту оның нормасын санның абсолюттік мәніне масштабтайды. Яғни, егер α нақты болып табылады

${ displaystyle lVert alpha q rVert = left | alpha right | , lVert q rVert ~.}$

Бұл норма болатындығының ерекше жағдайы мультипликативті, бұл дегеніміз

${ displaystyle lVert pq rVert = lVert p rVert , lVert q rVert}$

кез келген екі кватернион үшін б және q. Мультипликативтілік - бұл өнімнің конъюгаты формуласының нәтижесі, сонымен қатар ол сәйкестіктен туындайды

${ displaystyle det { Bigl (} { begin {array} {cc} a + ib & id + c id-c & a-ib end {array}} { Bigr)} = a ^ {2} + b ^ {2} + c ^ {2} + d ^ {2},}$

(қайда мен әдеттегіді білдіреді ойдан шығарылған бірлік ) және, демек, -ның көбейтінді қасиетінен детерминанттар квадрат матрицалар.

Бұл норма анықтауға мүмкіндік береді қашықтық г.(б, q) арасында б және q олардың айырмашылығының нормасы ретінде:

${ displaystyle d (p, q) = lVert p-q rVert ~.}$

Бұл жасайды ℍ а метрикалық кеңістік. Қосу және көбейту метрикалық топологияда үздіксіз. Шынында да, кез-келген скаляр үшін оң а ол ұстайды

${ displaystyle lVert (p + ap_ {1} + q + aq_ {1}) - (p + q) rVert = a lVert p_ {1} + q_ {1} rVert ,.}$

Үздіксіздік қабылдаудан туындайды а шегінде нөлге дейін. Көбейтуге арналған сабақтастық да ұқсас.

Кватернион бірлігі

A кватернион бұл квотернион. Нөлдік емес кватернионды бөлу q оның нормасы бойынша бірлік кватернион шығарады Uq деп аталады versor туралы q:

${ displaystyle mathbf {U} q = { frac {q} { lVert q rVert}}.}$

Әрбір кватернионның а полярлық ыдырау ${ displaystyle q = lVert q rVert cdot mathbf {U} q}$.

Конъюгацияны және норманы қолдану арқылы анықтауға мүмкіндік береді өзара нөлдік емес кватернионның Кватернионның көбейтіндісі оның кері санымен 1-ге тең болуы керек, ал жоғарыда келтірілген ойлар көбейтіндісін білдіреді ${ displaystyle q}$ және ${ displaystyle q ^ {*} / left Vert q right | ^ {2}}$ 1-ге тең (көбейтудің кез-келген тәртібі үшін). Сонымен өзара туралы q деп анықталды

${ displaystyle q ^ {- 1} = { frac {q ^ {*}} { lVert q rVert ^ {2}}}.}$

Бұл екі кватернионды бөлуге мүмкіндік береді б және q екі түрлі жолмен (қашан q нөлге тең емес). Яғни, олардың мөлшері де болуы мүмкін p q⁻¹ немесе q⁻¹б ; тұтастай алғанда, көбейту ретіне байланысты сол өнімдер әртүрлі, тек ерекше жағдайды қоспағанда б және q бір-бірінің скалярлық еселіктері болып табылады (мұндағы жағдайды қамтиды б = 0). Демек, белгілеу б/q екіұшты, өйткені онда екендігі көрсетілмеген q солға немесе оңға бөлінеді (болсын q⁻¹ көбейеді б оның сол жағында немесе оң жағында).

Алгебралық қасиеттері

Кейли графигі туралы Q₈. Қызыл көрсеткілер оң жақта көбейтуді білдіреді мен, ал жасыл көрсеткілер оң жақта көбейтуді білдіреді j.

Жинақ ℍ барлық кватерниондар болып табылады векторлық кеңістік үстінен нақты сандар бірге өлшем  4.^[c] Кватерниондарды көбейту ассоциативті болып табылады және векторлық қосылуға бөлінеді, бірақ скалярлық жиынтықты қоспағанда, ол коммутативті емес. Демек, төрттіктер ℍ ауыстырылмайтын болып табылады, ассоциативті алгебра нақты сандардың үстінде. Сөйтсе де ℍ құрамында күрделі сандардың көшірмелері бар, бұл күрделі сандардың үстіндегі ассоциативті алгебра емес.

Кватерниондарды бөлуге болатындықтан, олар а түзеді алгебра бөлімі. Бұл а-ға ұқсас құрылым өріс көбейтудің ауыстырымдылығын қоспағанда. Шекті өлшемді ассоциативті алгебралар нақты сандарға өте сирек кездеседі. The Фробениус теоремасы дәл үшеуі бар екенін айтады: ℝ, ℂ, және ℍ. Норма кватериондарды а-ға айналдырады алгебра және реал бойынша бөлінген алгебралар өте сирек кездеседі: Гурвиц теоремасы тек төртеуі бар дейді: ℝ, ℂ, ℍ, және ${ displaystyle mathbb {O}}$ ( октониондар ). Төрттіктер де а алгебра және біртұтас емес Банах алгебрасы.

Q-тің үш өлшемді графигі₈. Қызыл, жасыл және көк көрсеткілер көбейтуді білдіреді мен, j, және ксәйкесінше. Анық болу үшін теріс сандарға көбейту алынып тасталады.

Себебі кез-келген екі базалық вектордың көбейтіндісі басқа базис векторы, жиынтығы плюс немесе минус {±1, ±мен, ±j, ±к} құрайды топ көбейту кезінде. Бұл емесабель тобы деп аталады кватернион тобы және белгіленеді Q₈.^[29] Нағыз топтық сақина туралы Q₈ сақина ℝ [С₈] бұл сегіз өлшемді векторлық кеңістік ℝ. Оның әр элементі үшін бір негіздік векторы бар Q₈. Кватерниондар изоморфты болып табылады сақина туралы ℝ [С₈] бойынша идеалды элементтері тудырады 1 + (−1), мен + (−мен) , j + (−j), және к + (−к). Мұнда айырмашылықтардың әрқайсысындағы бірінші мүше негіз элементтерінің бірі болып табылады 1, мен, j, және к, ал екінші мүше - базалық элементтердің бірі −1, −мен, −j, және −к, қосымшасының инверсиялары емес 1, мен, j, және к.

Кватерниондар және геометриясы ℝ³

Кватернионның векторлық бөлігін координаталық вектор ретінде түсіндіруге болады ℝ³; сондықтан кватерниондардың алгебралық амалдары геометриясын көрсетеді ℝ³. Векторлық нүкте мен көлденең көбейтінділер сияқты операцияларды кватерниондар арқылы анықтауға болады және бұл кеңістіктік векторлар пайда болған жерде кватернион тәсілдерін қолдануға мүмкіндік береді. Компьютерлік графикадағы кілт кадрларының бағдарын интерполяциялау кватерниондардың пайдалы қолданбасы болды.^[14]

Осы бөлімнің қалған бөлігі үшін мен, j, және к үш қиялды да білдіреді^[30] негіздік векторлары ℍ және үшін негіз ℝ³. Ауыстыру мен арқылы −мен, j арқылы −j, және к арқылы −к векторды өзінің аддитивіне кері жібереді, сондықтан векторының кері қосындысы оның кватерниондағы конъюгатасымен бірдей. Осы себепті конъюгацияны кейде деп атайды кеңістіктік кері.

Екі векторлық кватерниондар үшін б = б₁мен + c₁j + г.₁к және q = б₂мен + c₂j + г.₂к олардың нүктелік өнім, векторларына ұқсастығы бойынша ℝ³, болып табылады

${ displaystyle p cdot q = b_ {1} b_ {2} + c_ {1} c_ {2} + d_ {1} d_ {2} ~.}$

Оны компонентсіз түрде қалай білдіруге болады

${ displaystyle p cdot q = textstyle { frac {1} {2}} (p ^ {*} q + q ^ {*} p) = textstyle { frac {1} {2}} (pq ^ {*} + qp ^ {*}).}$

Бұл бұйымдардың скалярлық бөліктеріне тең pq^∗, qp^∗, б^∗q, және q^∗б. Олардың векторлық бөліктері әртүрлі болатындығын ескеріңіз.

The кросс өнім туралы б және q реттелген негізде анықталған бағытқа қатысты мен, j, және к болып табылады

${ displaystyle p times q = (c_ {1} d_ {2} -d_ {1} c_ {2}) mathbf {i} + (d_ {1} b_ {2} -b_ {1} d_ {2 }) mathbf {j} + (b_ {1} c_ {2} -c_ {1} b_ {2}) mathbf {k} ,.}$

(Бағдар белгіні анықтау үшін қажет екенін еске түсіріңіз.) Бұл өнімнің векторлық бөлігіне тең pq (кватериондар ретінде), сонымен қатар векторлық бөлігі −q^∗б^∗. Оның формуласы да бар

${ displaystyle p times q = textstyle { tfrac {1} {2}} (pq-qp).}$

Үшін коммутатор, [б, q] = pq − qp, екі векторлық кватериондардың бірін алады

${ displaystyle [p, q] = 2p рет q.}$

Жалпы, рұқсат етіңіз б және q кватерниондар болыңыз және жазыңыз

${ displaystyle p = p _ { text {s}} + p _ { text {v}},}$

${ displaystyle q = q _ { text {s}} + q _ { text {v}},}$

қайда б_с және q_с скалярлық бөліктер болып табылады және б_v және q_v векторлық бөліктері болып табылады б және q. Сонда бізде формула бар

${ displaystyle pq = (pq) _ { text {s}} + (pq) _ { text {v}} = (p _ { text {s}} q _ { text {s}} - p _ { мәтін {v}} cdot q _ { text {v}}) + (p _ { text {s}} q _ { text {v}} + q _ { text {s}} p _ { text {v} } + p _ { text {v}} times q _ { text {v}}).}$

Бұл кватернионды көбейтудің коммутативтілігі векторлық кватерниондарды көбейтуден туындайтындығын көрсетеді. Сондай-ақ, бұл екі кватернионның векторлық бөліктері коллинеар болған жағдайда ғана жүретіндігін көрсетеді. Гамильтон^[31] бұл өнім сфералық үшбұрыштың үшінші шыңын берілген екі төбеден және оларға байланысты доға ұзындықтарынан есептейтінін көрсетті, ол да нүктелердің алгебрасы болып табылады Эллиптикалық геометрия.

Кватерниондарды айналу кезінде анықтауға болады ℝ³ және шақырылды билер Гамильтон.^[31] Сондай-ақ қараңыз Кватерниондар және кеңістіктегі айналу кватерниондарды пайдаланып үш өлшемді айналуды модельдеу туралы көбірек ақпарат алу үшін.

Қараңыз Хансон (2005)^[32] кватериондарды визуализациялау үшін.

Матрицалық көріністер

Күрделі сандар болуы мүмкін сияқты матрица ретінде ұсынылған, сондықтан кватерниондар да мүмкін. Кватерниондарды бейнелеудің кем дегенде екі тәсілі бар матрицалар кватернионды қосу мен көбейту матрицалық қосылуға және сәйкес болатындай етіп матрицаны көбейту. Біреуі - 2 × 2 пайдалану күрделі матрицалар, ал екіншісі - 4 × 4 нақты матрицалар. Екі жағдайда да берілген ұсыну сызықтық байланысты бейнелеудің бір тұқымдасы болып табылады. Терминологиясында абстрактілі алгебра, Бұлар инъекциялық гомоморфизмдер бастап ℍ дейін матрицалық сақиналар M (2, ℂ) және M (4, ℝ), сәйкесінше.

2 × 2 күрделі матрицаларды қолдана отырып, кватернион а + би + cj + dk ретінде ұсынылуы мүмкін

${ displaystyle { begin {bmatrix} a + bi & c + di - c + di & a-bi end {bmatrix}}.}$

Бұл ұсыныстың келесі қасиеттері бар:

• Кез келген екеуін шектеу б, c және г. нөлге дейін бейнесін шығарады күрделі сандар. Мысалы, параметр c = г. = 0 күрделі сандардың диагональды кешенді матрицалық көрінісін және параметрін шығарады б = г. = 0 нақты матрицалық көріністі шығарады.
• Кватернионның нормасы (өнімнің квадрат түбірі оның конъюгатымен, күрделі сандар сияқты) анықтауыш сәйкес матрицаның.^[33]
• Кватернионның конъюгаты сәйкес келеді конъюгат транспозасы матрицаның
• Шектеу арқылы бұл ұсыныс ан изоморфизм кватерниондардың кіші тобы мен олардың бейнесі арасында СУ (2). Топологиялық тұрғыдан кватерниондар болып табылады 3-сфера, сондықтан SU (2) кеңістігі де 3-сфера болып табылады. Топ СУ (2) сипаттау үшін маңызды айналдыру жылы кванттық механика; қараңыз Паули матрицалары.
• Кватернион бірліктері мен Паули матрицалары арасында қатты байланыс бар. Сегіз кватерниондық матрицаны алу арқылы алыңыз а, б, c және г., олардың үшеуін нөлге, ал төртіншісін 1 немесе −1 етіп қой. Кез-келген екі Паули матрицасын көбейту әрқашан кватернион бірлік матрицасын шығарады, олардың барлығы −1 қоспағанда. Біреуі −1 арқылы алады мен² = j² = к² = i j k = −1; мысалы соңғы теңдік

${ displaystyle { begin {aligned} ijk = sigma _ {1} sigma _ {2} sigma _ {3} sigma _ {1} sigma _ {2} sigma _ {3} = - 1 end {aligned}}}$

4 × 4 нақты матрицаларды қолдана отырып, сол кватерионды қалай жазуға болады

${ displaystyle { begin {bmatrix} a & -b & -c & -d b & a & -d & c c & d & a & -b d & -c & b & a end {bmatrix}} = a { begin {bmatrix} 1 & 0 & 0 & 0 0 & 1 & 0 & 0 & 0 0 & 0 & 1 & 0 0 & 0 & 0 & 1 end {bmatrix}} + b { begin {bmatrix} 0 & -1 & 0 & 0 & 1 & 0 & 0 & 0 0 & 0 & 0 & -1 & 0 0 & 0 & 1 & 0 end {bmatrix}} + c { begin {bmatrix} 0 & 0 & -1 & 0 0 & 0 & 0 & 1 1 & 0 & 0 & 0 & 0 0 & -1 & 0 & 0 end {bmatrix}} + d { begin {bmatrix} 0 & 0 & 0 & -1 0 & 0 & -1 & 0 0 & 1 & 0 & 0 1 & 0 & 0 & 0 end {bmatrix}}.}$

Алайда, кватериондардың өкілдігі M (4, ℝ) бірегей емес. Мысалы, сол кватернионды келесі түрінде ұсынуға болады

${ displaystyle { begin {bmatrix} a & d & -b & -c - d & a & c & -b b & -c & a & -d c & b & d & a end {bmatrix}} = a { begin {bmatrix} 1 & 0 & 0 & 0 0 & 0 & 1 & 0 & 0 0 & 0 & 1 & 0 0 & 0 & 0 & 1 end {bmatrix}} + b { begin {bmatrix} 0 & 0 & -1 & 0 0 & 0 & 0 & -1 & 1 & 0 & 0 & 0 & 0 0 & 1 & 0 & 0 end {bmatrix}} + c { begin {bmatrix} 0 & 0 & 0 & -1 & 0 & 0 & 1 & 0 0 & -1 & 0 & 0 1 & 0 & 0 & 0 end {bmatrix}} + d { begin {bmatrix} 0 & 1 & 0 & 0 - 1 & 0 & 0 & 0 & 0 0 & 0 & 0 & -1 0 & 0 & 1 & 0 end {bmatrix}}.}$

Матрицалардың біреуі скалярлық бөлігін, ал қалған үшеуі қисық-симметриялы болатын 48 форманың жеке формасы бар. Дәлірек айтсақ, функцияның жіберілуі үшін осы симметрия шектеулерімен матрицаның төрт төртбұрышының 48 жиынтығы бар 1, мен, j, және к төртбұрыштағы матрицаларға гомоморфизм жатады, яғни кватерниондардың қосындылары мен туындыларын матрицалардың қосындылары мен көбейтінділеріне жібереді.^[34] Бұл көріністе кватернионның конъюгаты сәйкес келеді транспозициялау матрицаның Кватернионның төртінші қуаты - болып табылады анықтауыш сәйкес матрицаның. Жоғарыда келтірілген 2 × 2 кешенді көріністегі сияқты, күрделі сандарды тағы да коэффициенттерді шектеу арқылы шығаруға болады; мысалы, екі 2 × 2 блоктары бар блок диагональды матрицалар ретінде c = г. = 0.

Кватерниондардың әрбір 4 × 4 матрицалық көрінісі бірлік кватерниондардың көбейту кестесіне сәйкес келеді. Мысалы, жоғарыда келтірілген матрицаның соңғы көрінісі көбейту кестесіне сәйкес келеді

изоморфты болып табылады ${ displaystyle {a mapsto 1, b mapsto i, c mapsto j, d mapsto k }}$ - дейін

Кез-келген көбейту кестесін бірінші жолда және бағанда сәйкестендіруді және жол тақырыптарының белгілері баған тақырыптарына қарама-қарсы болуын шектеу, екінші баған үшін 3 таңдау болуы мүмкін (белгіге мән бермей), 2 мүмкін үшінші бағанға таңдау (белгіге мән берілмейді), төртінші бағанға 1 мүмкін таңдау (белгіге назар аудармау); бұл 6 мүмкіндікті құрайды. Содан кейін, екінші бағанды ​​оң немесе теріс, үшінші бағанды ​​оң немесе теріс, ал төртінші бағанды ​​оң немесе теріс деп таңдап алуға болады, бұл белгі үшін 8 мүмкіндік береді. Әріптердің орналасу мүмкіндіктерін және олардың белгілерін көбейту 48-ге тең болады. Содан кейін ауыстыру 1 бірге а, мен бірге б, j бірге c, және к бірге г. және жолдар мен баған тақырыптарын алып тастаудың матрицалық көрінісін береді а + б мен + c j + г. к.

Лагранждың төрт квадрат теоремасы

Лагранждың төрт квадраттық теоремасының бір дәлелі ретінде кватерниондар қолданылады сандар теориясы, онда теріс емес бүтін сан төрт бүтін квадраттардың қосындысы болып табылады. Лагранждың төрт квадрат теоремасы өзіндік талғампаз теорема болуымен қатар, математика сандар теориясынан тыс жерлерде пайдалы қосымшаларға ие. комбинаторлық дизайн теория. Кватернионға негізделген дәлелдеу қолданылады Хурвиц кватерниондары, аналогы бар барлық кватерниондар сақинасының қосындысы Евклидтік алгоритм.

Кватерниондар күрделі сандардың жұбы ретінде

Кватерниондарды жұп күрделі сандар түрінде ұсынуға болады. Осы тұрғыдан алғанда, кватерниондар қолдану нәтижесі болып табылады Кейли-Диксон құрылысы күрделі сандарға. Бұл күрделі сандардың нақты сандар жұбы ретінде құрылуын қорыту.

Келіңіздер ℂ² күрделі сандардың үстінен екі өлшемді векторлық кеңістік бол. Екі элементтен тұратын негізді таңдаңыз 1 және j. Вектор ℂ² негіз элементтері тұрғысынан жазылуы мүмкін 1 және j сияқты

${ displaystyle (a + bi) 1+ (c + di) mathbf {j} ,.}$

Егер біз анықтайтын болсақ j² = −1 және мен j = −j мен, онда біз үлестірім заңын пайдаланып екі векторды көбейте аламыз. Қолдану к өнімге арналған қысқартылған жазба ретінде мен j көбейтудің әдеттегі кватерниондар сияқты ережелеріне әкеледі. Демек, жоғарыда келтірілген күрделі сандардың векторы кватернионға сәйкес келеді а + b i + c j + г. к. Егер элементтерін жазатын болсақ ℂ² төртбұрыш ретіндегі жұптар мен кватерниондар болса, сәйкесінше сәйкес келеді

${ displaystyle (a + bi, c + di) leftrightarrow (a, b, c, d).}$

Square1 квадрат түбірлері

Күрделі сандарда ℂ, тек екі сан бар, мен және -мен, оның квадраты −1. Жылы ℍ минус біреуінің квадрат түбірлері өте көп: квадратнион ерітіндісі −1 квадрат түбірі үшін бірлік сфера жылы ℝ³. Мұны көру үшін рұқсат етіңіз q = а + б мен + c j + г. к кватернион болып, оның квадратын −1 деп санаңыз. Жөнінде а, б, c, және г., Бұл білдіреді

${ displaystyle a ^ {2} -b ^ {2} -c ^ {2} -d ^ {2} = - 1,}$

${ displaystyle 2ab = 0,}$

${ displaystyle 2ac = 0,}$

${ displaystyle 2ad = 0.}$

Соңғы үш теңдеуді де қанағаттандыру үшін а = 0 немесе б, c, және г. барлығы 0. 0. Соңғысы мүмкін емес, өйткені а нақты сан болып табылады және бірінші теңдеу мұны білдіреді а² = −1. Сондықтан, а = 0 және б² + c² + г.² = 1. Басқаша айтқанда: Кватернион norm1-ге квадрат береді, егер ол векторлық кватернион болса, нормасы 1 болады. Анықтама бойынша барлық осындай векторлардың жиынтығы бірлік сфераны құрайды.

Теріс нақты кватериондардың ғана квадрат түбірлері шексіз көп. Басқаларының барлығында тек екеуі бар (немесе 0 жағдайында біреуі).^{[дәйексөз қажет ][d]}

ℍ күрделі ұшақтар одағы ретінде

−1 квадрат түбірлерінің әр жұбы төрттіктердің ішіндегі күрделі сандардың нақты көшірмесін жасайды. Егер q² = −1, then the copy is determined by the function

${displaystyle a+b{sqrt {-1,}}mapsto a+bq,.}$

In the language of абстрактілі алгебра, each is an инъекциялық сақина гомоморфизм бастап ℂ дейін ℍ. The images of the embeddings corresponding to q және -q бірдей.

Every non-real quaternion determines a planar subspace in ℍ that is isomorphic to ℂ: Write q as the sum of its scalar part and its vector part:

${displaystyle q=q_{s}+{vec {q}}_{v}.}$

Decompose the vector part further as the product of its norm and its versor:

${displaystyle q=q_{s}+lVert {vec {q}}_{v} Vert cdot mathbf {U} {vec {q}}_{v}.}$

(Note that this is not the same as ${displaystyle q_{s}+lVert q Vert cdot mathbf {U} q}$.) The versor of the vector part of q, ${displaystyle mathbf {U} {vec {q}}_{v}}$, is a right versor with –1 as its square. Therefore, it determines a copy of the complex numbers by the function

${displaystyle a+b{sqrt {-1,}}mapsto a+bmathbf {U} {vec {q}}_{v},.}$

Under this function, q is the image of the complex number ${displaystyle q_{s}+lVert {vec {q}}_{v} Vert i}$. Осылайша ℍ болып табылады одақ of complex planes intersecting in a common нақты сызық, where the union is taken over the sphere of square roots of minus one, bearing in mind that the same plane is associated with any pair of antipodal points on the sphere of right versors.

Commutative subrings

The relationship of quaternions to each other within the complex subplanes of ℍ can also be identified and expressed in terms of ауыстырмалы subrings. Specifically, since two quaternions б және q commute (i.e., p q = q p) only if they lie in the same complex subplane of ℍ, the profile of ℍ as a union of complex planes arises when one seeks to find all commutative subrings of the quaternion сақина. This method of commutative subrings is also used to profile the split-quaternions, which as an algebra over the reals are isomorphic to 2 × 2 нақты матрицалар.

Functions of a quaternion variable

The Julia sets and Mandelbrot sets can be extended to the Quaternions, but they must use cross sections to be rendered visually in 3 dimensions. This Julia set is cross sectioned at the x y ұшақ.

Like functions of a күрделі айнымалы, functions of a quaternion variable suggest useful physical models. For example, the original electric and magnetic fields described by Maxwell were functions of a quaternion variable. Examples of other functions include the extension of the Mandelbrot орнатылды және Julia sets into 4 dimensional space.^[36]

Exponential, logarithm, and power functions

Given a quaternion,

${displaystyle q=a+bmathbf {i} +cmathbf {j} +dmathbf {k} =a+mathbf {v} }$

the exponential is computed as^[37]

${displaystyle exp(q)=sum _{n=0}^{infty }{frac {q^{n}}{n!}}=e^{a}left(cos |mathbf {v} |+{frac {mathbf {v} }{|mathbf {v} |}}sin |mathbf {v} | ight)~~}$

and the logarithm is^[37]

${displaystyle ln(q)=ln |q|+{frac {mathbf {v} }{|mathbf {v} |}}arccos {frac {a}{|q|}}~~}$

It follows that the polar decomposition of a quaternion may be written

${displaystyle q=|q|e^{{hat {n}}varphi }=|q|left(cos(varphi )+{hat {n}}sin(varphi ) ight),}$

қайда бұрыш ${ displaystyle varphi}$^[e]

${displaystyle a=|q|cos(varphi )}$

and the unit vector ${displaystyle {hat {n}}}$ is defined by:

${displaystyle mathbf {v} ={hat {n}}|mathbf {v} |={hat {n}}|q|sin(varphi ),.}$

Any unit quaternion may be expressed in polar form as ${displaystyle e^{{hat {n}}varphi }}$.

The күш of a quaternion raised to an arbitrary (real) exponent х береді:

${displaystyle q^{x}=|q|^{x}e^{{hat {n}}xvarphi }=|q|^{x}left(cos(xvarphi )+{hat {n}},sin(xvarphi ) ight)~.}$

Geodesic norm

The geodesic distance г._ж(б, q) between unit quaternions б және q ретінде анықталады:

${displaystyle d_{ ext{g}}(p,q)=lVert ln(p^{-1}q) Vert .}$^[39]

and amounts to the absolute value of half the angle subtended by б және q along a great arc туралы S³ sphere.This angle can also be computed from the quaternion нүктелік өнім without the logarithm as:

${displaystyle arccos(2(pcdot q)^{2}-1).}$

Three-dimensional and four-dimensional rotation groups

Сөз »конъюгация ", besides the meaning given above, can also mean taking an element а дейін r a r⁻¹ қайда р is some non-zero quaternion. Барлық elements that are conjugate to a given element (in this sense of the word conjugate) have the same real part and the same norm of the vector part. (Thus the conjugate in the other sense is one of the conjugates in this sense.)

Thus the multiplicative group of non-zero quaternions acts by conjugation on the copy of ℝ³ consisting of quaternions with real part equal to zero. Conjugation by a unit quaternion (a quaternion of absolute value 1) with real part cos(φ) is a rotation by an angle 2φ, the axis of the rotation being the direction of the vector part. The advantages of quaternions are:

• Avoiding gimbal lock, a problem with systems such as Эйлер бұрыштары.
• Faster and more compact than матрицалар.
• Nonsingular representation (compared with Euler angles for example).
• Pairs of unit quaternions represent a rotation in 4D space (see Rotations in 4 dimensional Euclidean space: Algebra of 4D rotations ).

The set of all unit quaternions (versors ) forms a 3-сфера S³ және а топ (а Өтірік тобы ) under multiplication, double covering топ SO(3,ℝ) of real orthogonal 3×3 матрицалар туралы анықтауыш 1 since екі unit quaternions correspond to every rotation under the above correspondence. Қараңыз plate trick.

The image of a subgroup of versors is a нүктелік топ, and conversely, the preimage of a point group is a subgroup of versors. The preimage of a finite point group is called by the same name, with the prefix екілік. For instance, the preimage of the icosahedral group болып табылады binary icosahedral group.

The versors' group is isomorphic to SU(2), the group of complex унитарлы 2×2 matrices of анықтауыш  1.

Келіңіздер A be the set of quaternions of the form а + б мен + c j + г. к қайда a, b, c, және г. are either all бүтін сандар or all half-integers. Жинақ A Бұл сақина (in fact a домен ) және а тор and is called the ring of Hurwitz quaternions. There are 24 unit quaternions in this ring, and they are the vertices of a regular 24 cell бірге Schläfli таңбасы {3,4,3}. They correspond to the double cover of the rotational symmetry group of the regular тетраэдр. Similarly, the vertices of a regular 600 cell with Schläfli symbol {3,3,5}  can be taken as the unit icosians, corresponding to the double cover of the rotational symmetry group of the regular icosahedron. The double cover of the rotational symmetry group of the regular октаэдр corresponds to the quaternions that represent the vertices of the disphenoidal 288-cell.

Quaternion algebras

The Quaternions can be generalized into further algebras called quaternion algebras. Ал F to be any өріс with characteristic different from 2, and а және б to be elements of F; a four-dimensional unitary ассоциативті алгебра can be defined over F with basis 1, мен, j, және i j, қайда мен² = а, j² = б және i j = −j i (so (i j)² = −a b).

Quaternion algebras are isomorphic to the algebra of 2×2 матрицалар аяқталды F or form division algebras аяқталды F, depending on the choice of а және б.

Quaternions as the even part of Cl_3,0(ℝ)

The usefulness of quaternions for geometrical computations can be generalised to other dimensions by identifying the quaternions as the even part Cl⁺
_3,0(ℝ) туралы Клиффорд алгебрасы Cl_3,0(ℝ). This is an associative multivector algebra built up from fundamental basis elements σ₁, σ₂, σ₃ using the product rules

${displaystyle sigma _{1}^{2}=sigma _{2}^{2}=sigma _{3}^{2}=1,}$

${displaystyle sigma _{i}sigma _{j}=-sigma _{j}sigma _{i}qquad (j eq i).}$

If these fundamental basis elements are taken to represent vectors in 3D space, then it turns out that the шағылысу вектордың р in a plane perpendicular to a unit vector w can be written:

${displaystyle r^{prime }=-w,r,w.}$

Two reflections make a rotation by an angle twice the angle between the two reflection planes, so

${displaystyle r^{prime prime }=sigma _{2}sigma _{1},r,sigma _{1}sigma _{2}}$

corresponds to a rotation of 180° in the plane containing σ₁ және σ₂. This is very similar to the corresponding quaternion formula,

${displaystyle r^{prime prime }=-mathbf {k} ,r,mathbf {k} .}$

In fact, the two are identical, if we make the identification

${displaystyle mathbf {k} =sigma _{2}sigma _{1},,quad mathbf {i} =sigma _{3}sigma _{2},,quad mathbf {j} =sigma _{1}sigma _{3},,}$

and it is straightforward to confirm that this preserves the Hamilton relations

${displaystyle mathbf {i} ^{2}=mathbf {j} ^{2}=mathbf {k} ^{2}=mathbf {i,j,k} =-1~.}$

In this picture, so-called "vector quaternions" (that is, pure imaginary quaternions) correspond not to vectors but to bivectors – quantities with magnitude and orientations associated with particular 2D ұшақтар rather than 1D бағыттар. The relation to күрделі сандар becomes clearer, too: in 2D, with two vector directions σ₁ және σ₂, there is only one bivector basis element σ₁σ₂, so only one imaginary. But in 3D, with three vector directions, there are three bivector basis elements σ₁σ₂, σ₂σ₃, σ₃σ₁, so three imaginaries.

This reasoning extends further. In the Clifford algebra Cl_4,0(ℝ), there are six bivector basis elements, since with four different basic vector directions, six different pairs and therefore six different linearly independent planes can be defined. Rotations in such spaces using these generalisations of quaternions, called роторлар, can be very useful for applications involving homogeneous coordinates. But it is only in 3D that the number of basis bivectors equals the number of basis vectors, and each bivector can be identified as a жалған вектор.

There are several advantages for placing quaternions in this wider setting:^[40]

• Rotors are a natural part of geometric algebra and easily understood as the encoding of a double reflection.
• In geometric algebra, a rotor and the objects it acts on live in the same space. This eliminates the need to change representations and to encode new data structures and methods, which is traditionally required when augmenting linear algebra with quaternions.
• Rotors are universally applicable to any element of the algebra, not just vectors and other quaternions, but also lines, planes, circles, spheres, rays, and so on.
• Ішінде conformal model of Euclidean geometry, rotors allow the encoding of rotation, translation and scaling in a single element of the algebra, universally acting on any element. In particular, this means that rotors can represent rotations around an arbitrary axis, whereas quaternions are limited to an axis through the origin.
• Rotor-encoded transformations make interpolation particularly straightforward.
• Rotors carry over naturally to Pseudo-Euclidean spaces, for example, the Минковский кеңістігі туралы арнайы салыстырмалылық. In such spaces rotors can be used to efficiently represent Lorentz boosts, and to interpret formulas involving the gamma matrices.

For further detail about the geometrical uses of Clifford algebras, see Геометриялық алгебра.

Brauer group

The quaternions are "essentially" the only (non-trivial) орталық қарапайым алгебра (CSA) over the real numbers, in the sense that every CSA over the reals is Brauer equivalent to either the reals or the quaternions. Explicitly, the Brauer group of the reals consists of two classes, represented by the reals and the quaternions, where the Brauer group is the set of all CSAs, up to equivalence relation of one CSA being a matrix ring over another. Бойынша Artin–Wedderburn theorem (specifically, Wedderburn's part), CSAs are all matrix algebras over a division algebra, and thus the quaternions are the only non-trivial division algebra over the reals.

CSAs – rings over a field, which are simple algebras (have no non-trivial 2-sided ideals, just as with fields) whose center is exactly the field – are a noncommutative analog of extension fields, and are more restrictive than general ring extensions. The fact that the quaternions are the only non-trivial CSA over the reals (up to equivalence) may be compared with the fact that the complex numbers are the only non-trivial field extension of the reals.

Баға ұсыныстары

I regard it as an inelegance, or imperfection, in quaternions, or rather in the state to which it has been hitherto unfolded, whenever it becomes or seems to become necessary to have recourse to x, y, z, т.б.

— Уильям Роуэн Гамильтон^[41]

Time is said to have only one dimension, and space to have three dimensions. ... The mathematical quaternion partakes of both these elements; in technical language it may be said to be "time plus space", or "space plus time": and in this sense it has, or at least involves a reference to, four dimensions. And how the One of Time, of Space the Three, Might in the Chain of Symbols girdled be.

— Уильям Роуэн Гамильтон^{[42][толық дәйексөз қажет ]}

Quaternions came from Hamilton after his really good work had been done; and, though beautifully ingenious, have been an unmixed evil to those who have touched them in any way, including Clerk Maxwell.

— W. Thompson, Lord Kelvin (1892)^{[дәйексөз қажет ]}

I came later to see that, as far as the vector analysis I required was concerned, the quaternion was not only not required, but was a positive evil of no inconsiderable magnitude; and that by its avoidance the establishment of vector analysis was made quite simple and its working also simplified, and that it could be conveniently harmonised with ordinary Cartesian work.

— Оливер Хивисайд (1893)^[43]

Neither matrices nor quaternions and ordinary vectors were banished from these ten [additional] chapters. For, in spite of the uncontested power of the modern Tensor Calculus, those older mathematical languages continue, in my opinion, to offer conspicuous advantages in the restricted field of special relativity. Moreover, in science as well as in every-day life, the mastery of more than one language is also precious, as it broadens our views, is conducive to criticism with regard to, and guards against hypostasy [weak-foundation] of, the matter expressed by words or mathematical symbols.

— Ludwik Silberstein (1924)^{[44][толық дәйексөз қажет ]}

... quaternions appear to exude an air of nineteenth century decay, as a rather unsuccessful species in the struggle-for-life of mathematical ideas. Mathematicians, admittedly, still keep a warm place in their hearts for the remarkable algebraic properties of quaternions but, alas, such enthusiasm means little to the harder-headed physical scientist.

— Simon L. Altmann (1986)^[45]

Сондай-ақ қараңыз

Ескертулер

Әдебиеттер тізімі

Сыртқы мақалалар мен ресурстар

Кітаптар мен басылымдар

Сілтемелер мен монографиялар