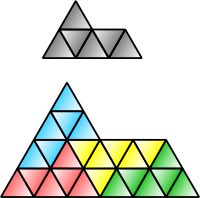
Қаптау - Rep-tile
Ішінде геометрия туралы tessellations, а қайтадан жабу немесе рептилия болуы мүмкін пішін бөлшектелген бірдей пішіндегі кішірек көшірмелерге. Термин а ретінде енгізілді сөз жануарларға бауырымен жорғалаушылар арқылы рекреациялық математик Соломон В. Голомб және танымал болды Мартин Гарднер оның «Математикалық ойындар «бағанының 1963 жылғы мамырдағы санында Ғылыми американдық.[1] 2012 жылы репликаларды жалпылау деп аталды өздігінен плиткалар жиынтығы арқылы енгізілді Ли Саллоу жылы Математика журналы.[2]
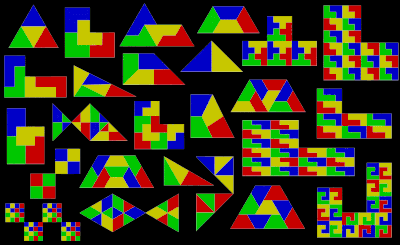
Терминология
Қайта плитка реплика деп белгіленгенn егер диссекция қолданса n көшірмелер Мұндай пішін міндетті түрде прототилді жазықтықтың плиткасы үшін, көптеген жағдайларда an апериодты плитка. Бастапқы пішіннің әр түрлі өлшемдерін қолдана отырып, плиткалық диссекцияны тұрақты емес плитка немесе иррептиль деп атайды. Егер диссекция қолданса n дана, пішіні сәйкес келмейтінn. Егер барлық осы ішкі плиткалар әр түрлі мөлшерде болса, онда плиткалар қосымша мінсіз деп сипатталады. Қайта пішінn немесе дұрыс емесn тривиальды түрде де маңызды емес (кн − к + n) кез келген үшін к > 1, ең кішкентай тақтайшаны ауыстыру арқылыn бөлу n тіпті кішірек плиткалар. Плиткаларды немесе плиткаларды қолданған кезде пішіннің орналасу реті - бұл мүмкін болатын плиткалардың ең аз саны.[3]
Мысалдар

Әрқайсысы шаршы, тіктөртбұрыш, параллелограмм, ромб, немесе үшбұрыш реп-4. The сфинкс hexiamond (жоғарыда суреттелген) реп-4 және реп-9 болып табылады, және олар аз ғана белгілердің бірі болып табылады өздігінен қайталанатын бесбұрыштар. The Госпер аралы реп-7 болып табылады. The Кох снежинкасы irrep-7: бірдей мөлшердегі алты ұсақ снежинкалар, кішігірім аудандарынан үш есе үлкен басқа снежинкамен бірге, біртұтас үлкен снежинаны құра алады.
A тік бұрышты үшбұрыш 1: 2 пропорциясындағы бүйірлік ұзындықтармен реп-5, ал оның реп-5 диссекциясы апериодтық негіз болып табылады дөңгелекті плитка. Авторы Пифагор теоремасы, гипотенуза, немесе реп-5 үшбұрышының көлбеу жағының ұзындығы бар √5.
Халықаралық стандарт ISO 216 көмегімен қағаз парақтарының өлшемдерін анықтайды √2, онда тікбұрышты парақтың ұзын жағы екінің квадрат түбірі қағаздың қысқа жағын бірнеше рет көрсетіңіз. Бұл пішіндегі төртбұрыштар реп-2 болып табылады. Тік төртбұрыш (немесе параллелограмм) -n егер ол арақатынасы болып табылады √n: 1. Ан тең бүйірлі тікбұрыш үшбұрышы да реп-2.
Плиткалар мен симметрия
Сияқты бірнеше тақтайшалар шаршы және тең бүйірлі үшбұрыш, болып табылады симметриялы және қашан да бірдей болып қалады айнада көрсетілген. Басқалары, сияқты сфинкс, болып табылады асимметриялық және бар екі нақты форма айна шағылыстырумен байланысты. Сфинксті және басқа да асимметриялық репликаларды бөлшектеу бастапқы пішінді де, оның айна кескінін де қажет етеді.
Плиткалар мен полиформалар
Кейбір плиткалар негізделген полиформалар сияқты полиамаздар және полиомино, немесе төсеу арқылы жасалған кескіндер тең бүйірлі үшбұрыштар және квадраттар шетінен шетіне дейін.
Квадраттар
Егер полиомино түзетуге болатын болса, яғни а тіктөртбұрыш, содан кейін ол реплика болады, өйткені тіктөртбұрыш бүйірлік ұзындықтың бүтін қатынасына ие болады және осылайша а плиткасын қояды шаршы. Мұны көруге болады октомино сегіз квадраттан жасалған. Екі октоминоның екі көшірмесі квадрат тақтайшасын жабады; сондықтан бұл октомино да реп-16 реплика болып табылады.

Төрт данасы нономино және nonakings шаршыға плитка төсейтін болады, сондықтан полиформалар реп-36 репликалары болып табылады.

Тең бүйірлі үшбұрыштар
Сол сияқты, егер а полиамаз теңбүйірлі үшбұрышты плиткалармен қаптаса, ол тағы да плитка болады.

 Үш теңбүйірлі үшбұрышқа негізделген балық тәрізді реплика | 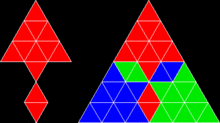 Он екі гауһар тастан жасалған ракетаға ұқсас тақтайша немесе жиектен шетіне (және бұрыштан бұрышқа) қойылған он екі тең бүйірлі үшбұрыш |
Тік бұрышты үшбұрыштар
A тік бұрышты үшбұрыш бір тік бұрышы 90 ° болатын үшбұрыш. Тік бұрышты үшбұрыштың екі формасы 45 ° -90 ° -45 ° үшбұрышы және 30 ° -60 ° -90 ° үшбұрышы зерттеушілердің назарын аударды.
45 ° -90 ° -45 ° үшбұрыштар
Негізделген полиформалар тең бүйірлі тікбұрыштар, жақтары 1: 1 қатынасында:√2, ретінде белгілі полиаболалар. Олардың шексіз саны - қайталанатын плиткалар. Шынында да, барлық қарапайым тақтайшалардың ішіндегі ең қарапайымы - бір қабырғалы тікбұрышты үшбұрыш. Ол реп-2-ге тең бұрышты екіге бөлетін бір түзуге бөлінгенде шығады гипотенуза. Rep-2 репликалары сонымен қатар реп-2 болып табыладыn және реп-4,8,16 + үшбұрыштары қосымша тақтайшалар береді. Бұлар қосалқы көшірмелердің жартысын тастап, қалғанын сол болғанша ауыстыру арқылы табылады айна-симметриялы тік бұрышты үшбұрыш ішінде. Басқаша айтқанда, екі көшірме тікбұрышты үшбұрышпен қаптайды. Осы жаңа репликалардың бірі үшеуінен пайда болған балықты еске түсіреді тең бүйірлі үшбұрыштар.
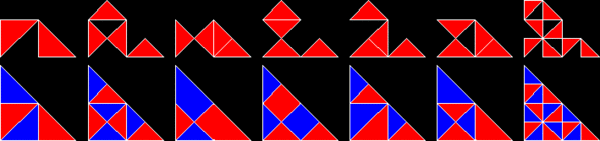
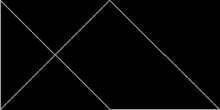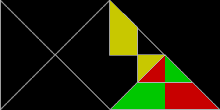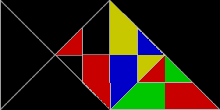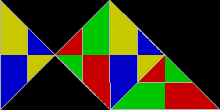
30 ° -60 ° -90 ° үшбұрыштар
30 ° -60 ° -90 ° тік бұрышты үшбұрыштарға негізделген полиформалар, олардың қабырғалары 1 қатынасында:√3 : 2, ретінде белгілі полидрафтерлер. Кейбіреулері ұқсас полимино және полиамаздар, басқалары ерекше.[4]
 Тридрафтер немесе үш 30-60-90 ° үшбұрыштан жасалған пішін. |  Тредрафтер бауырымен жорғалаушы. |
 Төрт 30-60-90 ° үшбұрыштан жасалған тетрадрафтер немесе пішін. |  Тетрадрафтер рептилия ретінде. |
 Гексадрафтер немесе алты 30-60-90 ° үшбұрыштан жасалған пішін. |  Гексадрафтер рептилия ретінде. |
Көп және вариантты плиткалар
Көптеген қарапайым тақтайшаларn2 барлық оң бүтін мәндері үшінn. Атап айтқанда, бұл үшеуіне қатысты трапеция үш осьтік параллель алтыбұрыш үшін үш тең бүйірлі үшбұрыштан (L-тромино, L-тетромино және Р-пентомино) және сфинкс гексаймондтан жасалған.[5] Сонымен қатар, көптеген репликалар, әсіресе жоғары репликаларn, әртүрлі тәсілдермен өздігінен плиткамен қаптауға болады. Мысалы, реп-9 L-тетраминоның кем дегенде он төрт түрлі плиткасы бар. Реп-9 сфинкс гексаймондын плиткамен әр түрлі тәсілдермен қаптауға болады.
 Реп-9 L-тетроминоның вариантты плиткалары |  Реп-9 сфинксі гексаймондының әртүрлі репликалары |
Қабырғалары шексіз тақтайшалар

Қабырғалары шекті санды көпбұрыштар, бірақ шектерінің саны шексіз болатын кейбір пішіндер тағы да плиткалар бола алады. Мысалы, терагоникалық үшбұрыш немесе мүйізді үшбұрыш - реп-4. Бұл сонымен қатар а фракталдық плитка.
Бес бұрышты тақтайшалар
Үшбұрышты және төртбұрышты (төрт жақты) плиткалар жиі кездеседі, бірақ бесбұрышты тақтайшалар сирек кездеседі. Ұзақ уақыт бойы сфинкс белгілі бір ғана мысал деп кеңінен сенді, бірақ Неміс /Жаңа Зеландия математик Карл Шерер және американдық математик Джордж Сичерман көптеген пирамида және сфинкстің ұзартылған нұсқасын қоса, көптеген мысалдар тапты. Бұл бесбұрышты тақтайшалар суретте көрсетілген Math Magic американдық математик бақылайтын беттер Эрих Фридман.[6] Алайда, сфинкс және оның кеңейтілген нұсқалары - тең көшірмелермен қапталған жалғыз бесбұрыш. Бауырымен жорғалаушылар.
 Карл Шерер ашқан бес бұрышты реплика |
Плиткалар мен фракталдар
Фрактал ретіндегі плиткалар
Қайта плиткаларды жасау үшін пайдалануға болады фракталдар немесе пішіндер өзіне ұқсас кішірек және кіші масштабтарда. Қайталама плиткалы фрактал қайта тақтайшаны бөлу, бөлінген пішіннің бір немесе бірнеше көшірмесін алып тастау, содан кейін жалғастыру арқылы пайда болады. рекурсивті. Мысалы, Sierpinski кілемі квадратты қайта қаптаудан 27 кіші квадратқа осылай түзілген және Сиерпинский үшбұрышы тең бүйірлі үшбұрыштың қайталануынан төрт кіші үшбұрышқа түзіледі. Бір ішкі көшірме жойылған кезде, қайталама-4 L-триомино төрт фрактал құруға болады, оның екеуі қоспағанда, бірдей бағдар.
 L-триоминоны геометриялық бөлшектеу (реп-4) |  L-триомино негізіндегі фрактал (реп-4) |
 L-триоминоға негізделген тағы бір фрактал |  L-триоминоға негізделген тағы бір фрактал |
Фракталдар плитка ретінде
Себебі фракталдар кішірек және кішігірім масштабтарда өздеріне ұқсас, олардың көпшілігі плитка тәрізді көшірмелер түрінде ыдырауы мүмкін. Алайда, егер фракталда бос болса интерьер, бұл ыдырау бүкіл жазықтықтың плиткасына әкелмеуі мүмкін. Мысалы, Сиерпинский үшбұрышы реп-3, үш данамен қапталған және Sierpinski кілемі сегіз данамен қапталған реп-8, бірақ бұл ыдыраудың қайталануы плитка жасамайды. Екінші жағынан, айдаһар қисығы Бұл кеңістікті толтыратын қисық бос емес интерьерімен; ол реп-4 және плитканы құрайды. Сол сияқты Госпер аралы кеңістікті толтыратын Gosper қисығынан пайда болған реп-7 болып табылады және қайтадан плитка түзеді.
Құрылысы бойынша кез-келген фракталдың ан қайталанатын функция жүйесі бірдей қатынастағы келісімшарттық карталардың rep-n.
 Sierpinski үшбұрышының үш кіші көшірмесіне негізделген Sierpinski үшбұрышы |  Sierpinski кілемінің сегіз кіші көшірмесіне негізделген Sierpinski кілемі |  Айдаһар қисығының 4 кіші көшірмесіне негізделген айдаһар қисығы |
Шексіз плитка
Кәдімгі көпбұрыштардың ішінен тек үшбұрыш пен квадратты олардың бірдей өлшемді көшірмелеріне бөлуге болады. Алайда, тұрақты алтыбұрыш алты тең бүйірлі үшбұрышқа бөлуге болады, олардың әрқайсысы кәдімгі алтыбұрышқа және тағы үш тең бүйірлі үшбұрышқа бөлінуі мүмкін. Бұл шексіздіктің негізі плитка төсеу алты бұрышты алтыбұрыштың. Алтыбұрыш ан irrep-∞ немесе ирреп-шексіздік иррептильді.

Сондай-ақ қараңыз
Ескертулер
Әдебиеттер тізімі
- Гарднер, М. (2001), «Плиткалар», Математиканың ауқымды кітабы: классикалық жұмбақтар, парадокстар және есептер, Нью-Йорк: В.В. Нортон, 46-58 бб
- Гарднер, М. (1991), «19 тарау: репликалар, жазықтықтағы фигураларды қайталау», Күтпеген ілу және басқа математикалық ауытқулар, Чикаго, Ил: Чикаго университетінің баспасы, 222–233 бб
- Langford, C. D. (1940), «Геометриялық жұмбақтың қолданылуы», Математикалық газет, 24 (260): 209–211, дои:10.2307/3605717
- Niţică, Viorel (2003), «Плиткалар қайта қаралды», MASS таңдау, Providence, RI: Американдық математикалық қоғам, 205–217 б., МЫРЗА 2027179
- Сэллоус, Ли (2012), «Өздігінен плиткалар жиынтығы туралы», Математика журналы, 85 (5): 323–333, дои:10.4169 / math.mag.85.5.323, МЫРЗА 3007213
- Шерер, Карл (1987), Жорғалаушыларға және сабақтас жануарларға жұмбақ саяхат
- Уэллс, Д. (1991), Қызықты және қызықты геометрияның пингвин сөздігі, Лондон: Пингвин, 213–214 бб
Сыртқы сілтемелер
Плиткалар
- Математика орталығы Сфинкс альбомы: http://mathematicscentre.com/taskcentre/sphinx.htm
- Кларк, А.Л. «Рептилиялар». http://www.recmath.com/PolyPages/PolyPages/Reptiles.htm.
- Вайсштейн, Эрик В. «Плитка». MathWorld.
- http://www.uwgb.edu/dutchs/symmetry/reptile1.htm (1999)
- IFStile - репликаларды табуға арналған бағдарлама: https://ifstile.com