Көпмүшелік - Polynomial

Жылы математика, а көпмүшелік болып табылады өрнек тұратын айнымалылар (деп те аталады анықталмайды ) және коэффициенттер, бұл тек амалдарды ғана қамтиды қосу, азайту, көбейту, және теріс емес бүтін дәрежелеу айнымалылар. Бірыңғай анықталмаған көпмүшелікке мысал х болып табылады х2 − 4х + 7. Үш айнымалының мысалы х3 + 2xyz2 − yz + 1.
Көпмүшелер математика мен жаратылыстанудың көптеген салаларында кездеседі. Мысалы, олар қалыптастыру үшін қолданылады көпмүшелік теңдеулер, бастауыштан бастап көптеген мәселелерді кодтайды сөз проблемалары күрделі ғылыми мәселелерге; олар анықтау үшін қолданылады көпмүшелік функциялар, олар негізгі параметрлерден пайда болады химия және физика дейін экономика және әлеуметтік ғылымдар; олар қолданылады есептеу және сандық талдау басқа функцияларды жуықтау үшін. Жетілдірілген математикада құруға көпмүшеліктер қолданылады көпмүшелік сақиналар және алгебралық сорттары, олар орталық ұғымдар болып табылады алгебра және алгебралық геометрия.
Этимология
Сөз көпмүшелік екі түрлі тамырға қосылады: грек поли, «көп» деген мағынаны білдіреді және латынша номеннемесе аты. Бұл терминнен шыққан биномдық латын түбірін ауыстыру арқылы екі- грекпен поли-. Сөз көпмүшелік алғаш рет 17 ғасырда қолданылған.[1]
Белгілеу және терминология
The х көпмүшеде болатынды әдетте а деп атайды айнымалы немесе ан анықталмаған. Көпмүшені өрнек ретінде қарастырған кезде, х - бұл ешқандай мәні жоқ тұрақты белгі (оның мәні «анықталмаған»). Алайда, біреуін қарастырған кезде функциясы көпмүшемен анықталады, содан кейін х функцияның аргументін білдіреді, сондықтан «айнымалы» деп аталады. Көптеген авторлар осы екі сөзді бір-бірінің орнына қолданады.
Анықталмаған үшін бас әріптерді және байланысты функцияның айнымалыларына (немесе аргументтеріне) сәйкес кіші әріптерді қолдану әдеттегідей.[дәйексөз қажет ]
Көпмүшелік P анықталмаған х әдетте ретінде белгіленеді P немесе сол сияқты P(х). Формальды түрде көпмүшенің аты P, емес P(х), бірақ функционалды белгі P(х) көпмүшелік пен онымен байланысты функция арасындағы айырмашылық түсініксіз болған кезден басталады. Сонымен қатар, функционалды жазба көбінесе көпмүшені және оның анықталмағандығын бір фразада көрсету үшін пайдалы. Мысалы, «рұқсат етіңіз P(х) көпмүшелі бол «бұл стенография» болсын P анықталмаған жерде көпмүше болу хЕкінші жағынан, анықталмаған атауды атап өту қажет болмаған кезде, егер анықталмаған (дар) лардың аты көпмүшенің әр пайда болуында пайда болмаса, көптеген формулалар оңайырақ және оңай оқылады. .
Бір математикалық объект үшін екі жазба болуы екіұштылық, көпмүшеліктер үшін функционалды белгінің жалпы мағынасын қарастыру арқылы формальды түрде шешілуі мүмкін.Егер а санды, айнымалыны, басқа көпмүшені немесе кез-келген өрнекті, содан кейін білдіреді P(а) шартты түрде алмастырудың нәтижесін білдіреді а үшін х жылы P. Сонымен, көпмүше P функциясын анықтайды
қайсысы көпмүшелік функция байланысты P.Көбінесе, бұл белгіні қолданған кезде, солай болады деп ойлайды а бұл сан. Алайда оны қосу және көбейту анықталған кез-келген доменде (яғни кез келгенде) қолдануға болады сақина ). Атап айтқанда, егер а бұл көпмүше P(а) сонымен қатар көпмүше болып табылады.
Нақтырақ айтқанда, қашан а анықталмаған болып табылады х, содан кейін сурет туралы х осы функция бойынша көпмүше болады P өзі (ауыстыру х үшін х ештеңені өзгертпейді). Басқа сөздермен айтқанда,
бұл ресми түрде бір көпмүшеге арналған екі белгінің болуын ақтайды.
Анықтама
Көпмүше - бұл өрнек салынуы мүмкін тұрақтылар айнымалылар деп аталатын немесе көмегімен анықталмайтын белгілер қосу, көбейту және дәрежелеу а теріс емес бүтін сан күш. Кәдімгі қасиеттерін қолдану арқылы түрлендірілуі мүмкін осындай екі өрнек коммутативтілік, ассоциативтілік және тарату қосу және көбейту, бірдей көпмүшені анықтайтын ретінде қарастырылады.
Бірмүшеде анықталмаған көпмүше х түрінде әрқашан жазуға (немесе қайта жазуға) болады
қайда тұрақты және анықталмаған болып табылады.[2][3] «Белгісіз» сөзі осыны білдіреді ешқандай мәнді білдірмейді, дегенмен кез келген мән оны алмастыра алады. Осы алмастырудың нәтижесін ауыстырылған мәнмен байланыстыратын карта - а функциясы, а деп аталады көпмүшелік функция.
Пайдалану арқылы мұны неғұрлым қысқа етіп білдіруге болады жиынтық белгісі:
Яғни, көпмүшелік нөлге тең болуы немесе нөлге тең емес ақырлы санның қосындысы түрінде жазылуы мүмкін шарттар. Әрбір термин санның көбейтіндісінен тұрады - деп аталады коэффициент мерзімнің[a] - және теріс емес бүтін дәрежеге дейін көтерілген анықталмаған шектер саны.
Жіктелуі
Терминдегі анықталмаған көрсеткішті сол терминдегі анықталмаған дәреже деп атайды; мүшенің дәрежесі - бұл осы мүшеде анықталмаған дәрежелерінің қосындысы, ал көпмүшелік дәрежесі - нөлдік емес коэффициенті бар кез-келген мүшенің ең үлкен дәрежесі.[4] Себебі х = х1, анықталмаған дәрежесі жазбаша дәрежесіз бір.
Анықталмаған термин және анықталмаған көпмүшелік сәйкесінше а деп аталады тұрақты мерзім және а тұрақты көпмүшелік.[b] Тұрақты мүшенің және нөлге тең емес тұрақты көпмүшенің дәрежесі - 0, нөлдік полиномның дәрежесі 0 (оның ешқандай мүшесі жоқ) әдетте анықталмаған ретінде қарастырылады (бірақ төменде қараңыз).[5]
Мысалға:
термин. Коэффициент −5, анықталмаған болып табылады х және ж, дәрежесі х екіге тең, ал дәрежесі ж бір. Бүкіл мүшенің дәрежесі дегеніміз ондағы анықталмаған әрқайсысының дәрежелерінің қосындысы, сондықтан бұл мысалда дәреже мынада 2 + 1 = 3.
Бірнеше мүшелердің қосындысын құрғанда көпмүше шығады. Мысалы, төмендегі көпмүше:
Ол үш терминнен тұрады: біріншісі - екінші дәреже, екіншісі - бірінші дәреже, үшіншісі - нөлдік дәреже.
Шағын дәрежелі көпмүшелерге нақты атаулар берілді. Нөлдік дәреженің көпмүшесі - а тұрақты көпмүшелік, немесе жай а тұрақты. Бір, екі немесе үш дәрежелі көпмүшелер сәйкесінше сызықтық көпмүшелер, квадрат көпмүшелер және кубтық көпмүшелер.[4] Жоғары дәрежелер үшін нақты атаулар жиі қолданылмайды, дегенмен квартикалық көпмүше (төртінші дәреже үшін) және квинтикалық көпмүше (бес дәреже үшін) кейде қолданылады. Дәрежелердің атаулары көпмүшеге немесе оның шарттарына қолданылуы мүмкін. Мысалы, термин 2х жылы х2 + 2х + 1 квадраттық көпмүшеліктегі сызықтық мүше.
Терминдері мүлдем жоқ деп санауға болатын 0 көпмүшесін деп атайды нөлдік көпмүше. Басқа тұрақты көпмүшелерден айырмашылығы, оның дәрежесі нөлге тең емес. Керісінше, нөлдік полиномның дәрежесі анық анықталмаған немесе теріс (−1 немесе −∞) ретінде анықталған.[6] Нөлдік көпмүше бірегей, өйткені ол шексіз саны бар анықталмаған бірдегі көпмүшелік тамырлар. Нөлдік көпмүшенің графигі, f(х) = 0, болып табылады х-аксис.
Бірнеше анықталмаған көпмүшеліктер жағдайында көпмүшелер деп аталады біртекті туралы дәрежесі n егер бәрі оның нөлге тең емес шарттарының дәрежесі n. Нөлдік көпмүше біртекті, ал біртекті көпмүшелік ретінде оның дәрежесі анықталмаған.[c] Мысалға, х3ж2 + 7х2ж3 − 3х5 5 дәрежесі біртектес. Толығырақ ақпаратты мына жерден қараңыз Біртекті полином.
The ауыстыру құқығы қосу терминдерді кез-келген артықшылықты тәртіпке келтіру үшін қолданыла алады. Біреуі анықталмаған көпмүшеліктерде терминдер дәрежеге сәйкес «кему дәрежесінде» реттеледі х«, ең үлкен дәреже мерзімімен бірінші немесе» жоғарылау күші х«. Жоғарыдағы мысалдағы көпмүшелік кему дәрежесінде жазылған х. Бірінші тоқсанның коэффициенті бар 3, анықталмаған хжәне дәреже 2. Екінші тоқсанда коэффициент болып табылады −5. Үшінші тоқсан - тұрақты шама. Себебі дәрежесі нөлдік емес көпмүшенің кез келген бір мүшесінің ең үлкен дәрежесі, бұл көпмүшенің екінші дәрежесі бар.[7]
Анықталмаған бірдей терминдер бірдей дәрежеге көтерілген екі терминді «ұқсас терминдер» немесе «ұқсас терминдер» деп атайды және оларды біріктіріп, тарату құқығы, коэффициенті біріктірілген терминдердің коэффициенттерінің қосындысы болатын жалғыз мүшеге. Мүмкін, бұл коэффициентті 0 құрайды.[8] Көпмүшелерді нөлдік емес коэффициенттері бар мүшелер саны бойынша жіктеуге болады, сондықтан бірмүшелік көпмүшені а деп атайды мономиялық,[d] екі мүшелі көпмүше а деп аталады биномдық, және үш мүшелі көпмүше а деп аталады триномиялық. «Квадриномия» термині кейде төрт мерзімді көпмүшелік үшін қолданылады.
A нақты көпмүшелік - деген көпмүше нақты коэффициенттер. Ол а анықтау үшін қолданылған кезде функциясы, домен соншалықты шектелмеген. Алайда, а нақты көпмүшелік функция - бұл нақты көпмүшемен анықталатын реалдан реалға дейінгі функция. Сол сияқты бүтін көпмүше - деген көпмүше бүтін коэффициенттер және а күрделі көпмүшелік - деген көпмүше күрделі коэффициенттер.
Бір анықталмаған көпмүшені а деп атайды бірмәнді көпмүшелік, анықталмағаннан көп көпмүшені а деп атайды көп айнымалы көпмүшелік. Екі анықталмаған көпмүшені а деп атайды екі жақты көпмүшелік.[3] Бұл түсініктер жеке көпмүшеліктерге қарағанда көбіне жұмыс істейтін көпмүшеліктер түріне қатысты; мысалы, бір айнымалы көпмүшелермен жұмыс істеу кезінде тұрақты көпмүшеліктер (бұл тұрақты емес көпмүшелерді азайту нәтижесінде пайда болуы мүмкін) алынып тасталмайды, дегенмен, қатаң түрде айтсақ, тұрақты көпмүшелер анықталмаған болады. Көп айнымалы көпмүшелерді әрі қарай жіктеуге болады екі жақты, маңызды емесжәне т.с.с. рұқсат етілген анықталмағандардың максималды санына сәйкес. Тағы да, қарастырылып отырған объектілер жиыны азайту кезінде жабылатындай етіп, үш өлшемді көпмүшелерді зерттеу әдетте екі айнымалы көпмүшеліктерге және т.б. Сондай-ақ қарапайым «көпмүшеліктер» деп айтуға болады х, ж, және з«, рұқсат етілмеген анықтамаларды тізімге қосыңыз.
The көпмүшені бағалау сандық мәнді әр анықталмағанға ауыстырудан және көрсетілген көбейту мен толықтыруларды орындаудан тұрады. Анықталмаған бір полином үшін бағалау көбінесе тиімді болады (орындалатын арифметикалық амалдардың саны аз) Хорнер әдісі:
Арифметика
Қосу
Көмегімен полиномдарды қосуға болады ассоциативті құқық қосу (олардың барлық шарттарын бір сомаға біріктіру), содан кейін қайта реттеуге болады ( ауыстыру құқығы ) және ұқсас терминдерді біріктіру.[8][9] Мысалы, егер
- және
содан кейін қосынды
ретке келтіруге және қайта топтастыруға болады
содан кейін жеңілдетілген
Көпмүшелер бір-біріне қосылса, нәтижесі тағы бір көпмүше болады.[10]
Көбейту
Көпмүшелерді көбейтуге де болады. Кеңейту үшін өнім екі көпмүшенің ішінен мүшелер жиынтығына бөлу заңы бірнеше рет қолданылады, нәтижесінде бір көпмүшенің әрбір мүшесі екіншісінің әрбір мүшесіне көбейтіледі.[8] Мысалы, егер
содан кейін
Әр тоқсанда көбейтуді жүзеге асырады
Ұқсас терминдерді біріктіру нәтиже береді
оны жеңілдетуге болады
Мысалдағыдай, көпмүшелердің көбейтіндісі әрқашан көпмүшелік болады.[10][5]
Композиция
Көпмүшелік берілген бір айнымалы және басқа көпмүшелік ж кез келген айнымалы санының құрамы бірінші көпмүшенің айнымалысының әрбір көшірмесін екінші көпмүшеге ауыстыру арқылы алынады.[5] Мысалы, егер және содан кейін
Бөлім
Бір көпмүшенің екінші көпмүшеге бөлінуі әдетте көпмүше емес. Оның орнына мұндай коэффициенттер деп объектілердің неғұрлым жалпы отбасы болып табылады рационал бөлшектер, рационалды өрнектер, немесе рационалды функциялар, контекстке байланысты.[12] Бұл екеуінің арақатынасына ұқсас бүтін сандар Бұл рационалды сан, міндетті түрде бүтін сан емес.[13][14] Мысалы, бөлшек 1/(х2 + 1) көпмүшелік емес, және оны айнымалының дәрежелерінің ақырғы қосындысы түрінде жазуға болмайды х.
Бір айнымалыдағы көпмүшелер үшін, деген ұғым бар Көпмүшелердің эвклидтік бөлімі жалпылау Евклидтік бөлім бүтін сандар.[e] Бөлу туралы бұл түсінік а(х)/б(х) нәтижесінде екі көпмүше шығады, а мөлшер q(х) және а қалдық р(х), осылай а = б q + р және дәрежесі (р) <дәреже (б). Бағасы мен қалғаны бірнеше алгоритмдердің кез келгенімен есептелуі мүмкін, соның ішінде көпмүшелік ұзақ бөлу және синтетикалық бөлу.[15]
Бөлгіш болған кезде б(х) моникалық және сызықтық, яғни б(х) = х − c тұрақты үшін c, содан кейін көпмүшелік қалдық теоремасы бөлудің қалған бөлігі деп бекітеді а(х) арқылы б(х) болып табылады бағалау f(c).[14] Бұл жағдайда квотаны есептеуге болады Руффини ережесі, синтетикалық бөлінудің ерекше жағдайы.[16]
Факторинг
А-да коэффициенттері бар барлық көпмүшелер бірегей факторизация домені (мысалы, бүтін сандар немесе а өріс ) сонымен бірге көпмүшенің көбейтіндісі ретінде жазылатын дәлелденген формасы бар қысқартылмайтын көпмүшелер және тұрақты. Факторланған бұл форма факторлардың ретіне қарай және оларды өзгермейтін тұрақтыға көбейтуге дейін ерекше. Өрісі жағдайында күрделі сандар, төмендетілмейтін факторлар сызықтық болып табылады. Астам нақты сандар, олар бір немесе екі дәрежеге ие. Бүтін сандар мен рационал сандар төмендетілмейтін факторлардың кез-келген дәрежесі болуы мүмкін.[17] Мысалы,
болып табылады
бүтін сандар мен реалдың үстінде және
күрделі сандардың үстінде.
Факторланған форманы есептеу деп аталады факторизация тұтастай алғанда, қолмен есептеу арқылы орындау өте қиын. Алайда тиімді полиномдық факторизация алгоритмдер көпшілігінде қол жетімді компьютерлік алгебра жүйелері.
Есеп
Есептеу туындылар және функциялардың басқа түрлерімен салыстырғанда көпмүшеліктердің интегралдары ерекше қарапайым.The туынды көпмүшенің құрметпен х көпмүше
Коэффициенттері абстрактілі параметрлерден шыққан көпмүшеліктер үшін (мысалы, коэффициенттер бүтін сандар болса) модуль кейбіреулері жай сан б, немесе шартты сақинаның элементтері), туынды формуласын формальды, коэффициентпен түсіндіруге болады как қосындысын білдіретінін түсінді к дана ак. Мысалы, модуль бүтін сандарының үстінде б, көпмүшенің туындысы хб + х көпмүше болып табылады 1.[18]
Көпмүшелік функциялар
A көпмүшелік функция арқылы анықтауға болатын функция болып табылады бағалау көпмүше. Дәлірек айтқанда, функция f біреуі дәлел берілген доменнен көпмүшелік болса, көпмүшелік функция болады
деп бағалайды барлығына х ішінде домен туралы f (Мұнда, n теріс емес бүтін сан болып табылады және а0, а1, а2, ..., аn тұрақты коэффициенттер болып табылады).Әдетте, егер басқаша көрсетілмесе, көпмүшелік функциялары бар күрделі коэффициенттер, аргументтер және мәндер. Атап айтқанда, нақты коэффициенттерге шектелген көпмүшелік функцияны күрделі сандардан күрделі сандарға дейін анықтайды. Егер бұл функцияның домені де болса шектелген нәтижелер функциясы а нақты функция бұл реалдарды реалға бейнелейді.
Мысалы, функция f, арқылы анықталады
бір айнымалының көпмүшелік функциясы болып табылады. Бірнеше айнымалылардың көпмүшелік функциялары дәл осылай анықталады, мысалы бірнеше анықталмаған полиномдар қолданылады.
Көпмүшелік функциялардың анықтамасына сәйкес, көпмүшелік емес, бірақ көпмүшелік функцияларды анықтайтын өрнектер болуы мүмкін. Мысал ретінде өрнек келтіруге болады көпмүшелік сияқты мәндерді алады аралықта , демек, екі өрнек те осы интервалдағы бірдей көпмүшелік функцияны анықтайды.
Әрбір көпмүшелік функция үздіксіз, тегіс, және толығымен.
Графиктер

0 дәрежелі полином:
f(х) = 2
1 дәрежелі көпмүшелік:
f(х) = 2х + 1
2 дәрежелі полином:
f(х) = х2 − х − 2
= (х + 1)(х − 2)
3 дәрежелі полином:
f(х) = х3/4 + 3х2/4 − 3х/2 − 2
= 1/4 (х + 4)(х + 1)(х − 2)
4 дәрежелі көпмүшелік:
f(х) = 1/14 (х + 4)(х + 1)(х − 1)(х − 3)
+ 0.5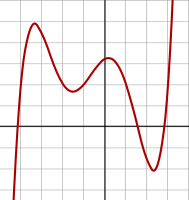
5 дәрежелі көпмүшелік:
f(х) = 1/20 (х + 4)(х + 2)(х + 1)(х − 1)
(х − 3) + 2
6 дәрежелі полином:
f(х) = 1/100 (х6 − 2х 5 − 26х4 + 28х3
+ 145х2 − 26х − 80)
7 дәрежелі көпмүшелік:
f(х) = (х − 3)(х − 2)(х − 1)(х)(х + 1)(х + 2)
(х + 3)
Бір нақты айнымалыдағы көпмүшелік функцияны а түрінде ұсынуға болады график.
- Нөлдік көпмүшенің графигі
- f(х) = 0
- болып табылады х-аксис.
- 0 көпмүшелік дәрежесінің графигі
- f(х) = а0, қайда а0 ≠ 0,
- көлденең сызық болып табылады ж-түсіну а0
- 1 дәрежелі көпмүшелік (немесе сызықтық функция) графигі
- f(х) = а0 + а1х , қайда а1 ≠ 0,
- - қиғаш сызық ж-түсіну а0 және көлбеу а1.
- 2 дәрежелі көпмүшенің графигі
- f(х) = а0 + а1х + а2х2, қайда а2 ≠ 0
- Бұл парабола.
- 3 дәрежелі көпмүшелік графигі
- f(х) = а0 + а1х + а2х2 + а3х3, қайда а3 ≠ 0
- Бұл текше қисық.
- Дәрежесі 2 немесе одан жоғары кез келген көпмүшенің графигі
- f(х) = а0 + а1х + а2х2 + ... + аnхn , қайда аn ≠ 0 және n ≥ 2
- үздіксіз сызықтық емес қисық болып табылады.
Тұрақты емес көпмүшелік функция шексіздікке ұмтылады айнымалы шексіз көбейгенде (in абсолютті мән ). Егер дәреже бірден жоғары болса, онда графикте жоқ асимптоталар. Оның екеуі бар параболалық тармақтар тік бағытта (оң үшін бір тармақ) х біреуі теріс х).
Полиномдық графиктер есептеулерде кесу, көлбеу, ойысу және соңғы мінез-құлықты қолдана отырып талданады.
Теңдеулер
A көпмүшелік теңдеу, деп те аталады алгебралық теңдеу, болып табылады теңдеу форманың[19]
Мысалға,
көпмүшелік теңдеу болып табылады.
Теңдеулерді қарастыру кезінде көпмүшелердің анықталмаған (айнымалысы) деп те аталады белгісіз, және шешімдер теңдік ақиқат болатын белгісіздердің мүмкін мәндері (жалпы бірнеше шешім болуы мүмкін). Көпмүшелік теңдеу а-ға қарама-қарсы тұрады көпмүшелік жеке басын куәландыратын сияқты (х + ж)(х − ж) = х2 − ж2, мұндағы екі өрнек те әр түрлі формада бір көпмүшені білдіреді және соның салдарынан екі мүшенің кез-келген бағасы жарамды теңдік береді.
Бастауышта алгебра, сияқты әдістер квадрат формула барлық бірінші және екінші дәрежелі полиномдық теңдеулерді бір айнымалыға шешуге үйретеді. Формулалары бар текше және кварталық теңдеулер. Жоғары дәрежелер үшін Абель-Руффини теоремасы радикалдарда жалпы формула болуы мүмкін емес деп санайды. Алайда, тамыр табу алгоритмдері табу үшін қолданылуы мүмкін сандық жуықтамалар кез келген дәрежедегі көпмүшелік өрнектің түбірлері.
Нақты коэффициенттері бар полиномдық теңдеудің шешімдерінің дәрежесі градустан аспауы мүмкін және күрделі шешімдер олармен есептеледі көптік. Бұл факт деп аталады алгебраның негізгі теоремасы.
Теңдеулерді шешу
Әрбір көпмүшелік P жылы х анықтайды а функциясы деп аталады көпмүшелік функция байланысты P; The теңдеу P(х) = 0 болып табылады көпмүшелік теңдеу байланысты P. Бұл теңдеудің шешімдері деп аталады тамырлар немесе көп функцияның нөлдері (олар функцияның графигі сәйкес келетін нүктелерге сәйкес келеді) х-аксис).
Сан а көпмүшенің түбірі P егер және егер болса сызықтық көпмүшелік х − а бөледі P, егер басқа көпмүше болса Q осындай P = (х – аQ). Бұл мүмкін х − а бөледі P бірнеше рет: егер (х − а)2 бөледі P содан кейін а а деп аталады бірнеше тамыр туралы Pжәне басқаша а а деп аталады қарапайым түбір туралы P. Егер P нөлге тең емес көпмүше, ең жоғарғы дәреже бар м осындай (х − а)м бөледі P, деп аталады көптік тамырдың а жылы P. Қашан P - нөлдік көпмүше, сәйкес көпмүшелік теңдеу тривиальды, және бұл жағдай, әдетте, түбірлерді қарастырғанда алынып тасталады, өйткені жоғарыда келтірілген анықтамалармен әр сан нөлдік көпмүшенің түбірі, анықталмаған еселігі бар. Осы қоспағанда, түбірлер саны P, тіпті олардың көбейтінділерімен есептелген, дәрежесінен аспауы керек P.[20] Көпмүшенің коэффициенттері мен оның түбірлері арасындағы байланыс сипатталады Вьетнамның формулалары.
Сияқты кейбір көпмүшелер х2 + 1, арасында тамырлар жоқ нақты сандар. Егер, дегенмен, қабылданған шешімдер жиынтығы келесіге дейін кеңейтіледі күрделі сандар, әр тұрақты емес көпмүшенің кем дегенде бір түбірі болады; Бұл алгебраның негізгі теоремасы. Факторларды дәйекті бөлу арқылы х − а, күрделі коэффициенттері бар кез-келген көпмүшені тұрақты (оның жетекші коэффициенті) рет 1-дегі осындай көпмүшелік факторлардың көбейтіндісі түрінде жазуға болатындығын көреді; осылайша, олардың еселіктерімен есептелген (күрделі) түбірлердің саны көпмүшелік дәрежесіне дәл тең.
«Теңдеуді шешудің» бірнеше мағынасы болуы мүмкін. Шешімдерді нақты сандар түрінде көрсеткісі келуі мүмкін; мысалы, бірегей шешімі 2х – 1 = 0 болып табылады 1/2. Өкінішке орай, бұл жалпы дәрежедегі теңдеулер үшін мүмкін емес, және ежелгі заманнан бері математиктер шешімдерді осылай өрнектеуге тырысты алгебралық өрнек; мысалы алтын коэффициент болып табылады Ежелгі уақытта олар тек бір және екі дәрежеге қол жеткізді. Үшін квадрат теңдеулер, квадрат формула шешімдердің осындай өрнектерін ұсынады. XVI ғасырдан бастап ұқсас формулалар (квадрат түбірлерге қосымша куб түбірлерін қолдану), бірақ одан да күрделі және үшінші және төртінші деңгей теңдеулерімен белгілі (қараңыз) текше теңдеу және кварталық теңдеу ). Бірақ 5-ші және одан жоғары дәрежеге арналған формулалар бірнеше ғасырлар бойы зерттеушілерден алыстап кетті. 1824 жылы, Нильс Генрик Абель шешімдері тек арифметикалық амалдар мен радикалдарды қамтитын (ақырлы) формуламен өрнектелмейтін 5 дәрежелі теңдеулер бар екендігінің керемет нәтижесін дәлелдеді (қараңыз) Абель-Руффини теоремасы ). 1830 жылы, Эварист Галуа төрттен жоғары дәрежелі теңдеулердің көпшілігін радикалдар шеше алмайтындығын дәлелдеді және әр теңдеу үшін оны радикалдар шешетіндігін, ал егер шешсе, шеше алатынын көрсетті. Бұл нәтиже басталды Галуа теориясы және топтық теория, қазіргі заманның екі маңызды саласы алгебра. Галуаның өзі оның әдісі бойынша жасалған есептеулер мүмкін еместігін атап өтті. Осыған қарамастан, 5 және 6 дәрежелі шешілетін теңдеулердің формулалары жарияланды (қараңыз) квинтикалық функция және секстикалық теңдеу ).
Түбірлерге арналған алгебралық өрнек болмаған кезде және мұндай алгебралық өрнек болған кезде, бірақ өте пайдалы болған кезде, шешудің ерекше тәсілі - есептеу сандық жуықтамалар шешімдер.[21] Бұл үшін көптеген әдістер бар; кейбіреулері көпмүшеліктермен шектеледі, ал басқалары кез-келгеніне қолданылуы мүмкін үздіксіз функция. Ең тиімді алгоритмдер оңай шешуге мүмкіндік береді (а компьютер ) дәрежесі 1000-нан жоғары полиномдық теңдеулер (қараңыз) Түбірлерді табу алгоритмі ).
Бірнеше анықталмаған көпмүшеліктер үшін полином функциясы нөл мәнін алатын айнымалылар үшін мәндердің комбинациясы жалпы деп аталады нөлдер «тамырлар» орнына. Көпмүшеліктердің нөлдер жиынын зерттеу объект болып табылады алгебралық геометрия. Бірнеше белгісіздердегі көпмүшелік теңдеулер жиынтығы үшін бар алгоритмдер олардың шектеулі саны бар-жоғын шешу күрделі шешімдер, ал егер бұл сан шектеулі болса, шешімдерді есептеу үшін. Қараңыз Көпмүшелік теңдеулер жүйесі.
Барлық көпмүшелер бірінші дәрежелі болатын ерекше жағдайды а деп атайды сызықтық теңдеулер жүйесі, ол үшін әр түрлі диапазон шешу әдістері бар, соның ішінде классикалық Гауссты жою.
Тек шешімдерге қызығушылық білдіретін полиномдық теңдеу бүтін сандар а деп аталады Диофантиялық теңдеу. Диофантиялық теңдеулерді шешу, әдетте, өте қиын мәселе. Кез-келген генерал болуы мүмкін емес екендігі дәлелденді алгоритм оларды шешуге, тіпті шешімдер жиынтығының бос екендігін шешуге арналған (қараңыз) Гильберттің оныншы мәселесі ). Соңғы елу жыл ішінде шешілген кейбір танымал есептер диофант теңдеулерімен байланысты, мысалы Ферманың соңғы теоремасы.
Жалпылау
Көпмүшелер ұғымының бірнеше жалпыламалары бар.
Тригонометриялық көпмүшелер
A тригонометриялық көпмүшелік ақырлы болып табылады сызықтық комбинация туралы функциялары күнә (nx) және cos (nx) бірге n бір немесе бірнеше мәндерді қабылдау натурал сандар.[22] Нақты бағаланатын функциялар үшін коэффициенттер нақты сандар ретінде қабылдануы мүмкін.
Егер күнә болса (nx) және cos (nx) күнә тұрғысынан кеңейтілген (х) және cos (х), тригонометриялық көпмүшелік екі айнымалыдағы көпмүшеге айналады sin (х) және cos (х) (қолдану Тригонометриялық сәйкестіліктер тізімі # Көп бұрышты формулалар ). Керісінше, күнәдағы әрбір көпмүше (х) және cos (х) түрлендірілуі мүмкін, Өнімнің жалпы сомасына сәйкестілігі, sin функцияларының сызықтық комбинациясына (nx) және cos (nx). Бұл эквиваленттік сызықтық комбинациялардың көпмүшеліктер деп аталуының себебін түсіндіреді.
Үшін күрделі коэффициенттер, мұндай функция мен ақырғы арасындағы айырмашылық жоқ Фурье сериясы.
Тригонометриялық көпмүшелер кеңінен қолданылады, мысалы тригонометриялық интерполяция қолданылды интерполяция туралы мерзімді функциялар. Олар сонымен қатар дискретті Фурье түрлендіруі.
Матрицалық көпмүшелер
A матрицалық полином - деген көпмүше квадрат матрицалар айнымалы ретінде.[23] Қарапайым, скалярлы көпмүшелік берілген
матрица бойынша бағаланған бұл көпмүшелік A болып табылады
қайда Мен болып табылады сәйкестік матрицасы.[24]
A матрицалық полиномдық теңдеу - бұл қарастырылып отырған нақты матрицалар үшін орындалатын екі матрицалық көпмүшелер арасындағы теңдік. A матрицалық полиномдық сәйкестілік бұл барлық матрицалар үшін орындалатын матрицалық полиномдық теңдеу A көрсетілгенде матрицалық сақина Мn(R).
Лоран көпмүшелері
Лоран көпмүшелері көпмүшелерге ұқсайды, бірақ айнымалының (тердің) теріс күштерінің пайда болуына мүмкіндік береді.
Рационалды функциялар
A рационал бөлшек болып табылады мөлшер (алгебралық бөлшек ) екі көпмүшенің. Кез келген алгебралық өрнек рационал бөлшек ретінде қайта жазуға болатын а рационалды функция.
Көпмүшелік функциялар айнымалылардың барлық мәндері үшін анықталса, рационал функция тек бөлгіш нөлге тең емес айнымалылар мәндері үшін анықталады.
Рационал бөлшектерге Лоран көпмүшелері кіреді, бірақ бөлгіштерді анықталмаған деңгейлермен шектемейді.
Қуат сериялары
Ресми қуат қатары көпмүшелерге ұқсайды, бірақ шексіз дәрежеге ие болмауы үшін шексіз көптеген нөлдік емес мүшелердің пайда болуына мүмкіндік береді. Көпмүшеліктен айырмашылығы, оларды нақты және толық жазу мүмкін емес (дәл сол сияқты) қисынсыз сандар мүмкін емес), бірақ олардың шарттарын манипуляциялау ережелері көпмүшеліктермен бірдей. Ресми емес қуат сериясы көпмүшелерді жалпылау, бірақ екі дәрежелік қатарды көбейту жақындамауы мүмкін.
Басқа мысалдар
Екінші айнымалы бірінші айнымалыға қолданылатын экспоненциалды функциямен алмастырылатын екі мәнді көпмүшелік P(х, eх), деп аталуы мүмкін экспоненциалды көпмүше.
Қолданбалар
Реферат алгебра
Жылы абстрактілі алгебра, біреуін ажыратады көпмүшелер және көпмүшелік функциялар. A көпмүшелік f бірінде анықталмаған х астам сақина R форманың формальды көрінісі ретінде анықталады
қайда n - бұл натурал сан, коэффициенттер а0, . . ., аn элементтері болып табылады R, және х ресми символ, оның күші хмен тек тиісті коэффициенттер үшін толтырғыштар амен, сондықтан берілген формальды өрнек тек ретті кодтау тәсілі болады (а0, а1, . . .), бар жерде n осындай амен = 0 барлығына мен > n. Мәнін бірдей бөлетін екі көпмүшелік n егер олардың коэффициенттерінің реттілігі тең болған жағдайда ғана тең деп саналады; бұдан басқа кез-келген көпмүшелік мәні үлкен кез-келген көпмүшеге тең n одан коэффициенті нөлге тең мүшелерді қосу арқылы алынған. Бұл көпмүшелерді тек сәйкес коэффициенттерді қосу арқылы қосуға болады (мұндай коэффициенттердің бар екендігіне көз жеткізу үшін нөлдік коэффициенттері бар шарттар бойынша кеңейту ережесін қолдануға болады). Осылайша, әрбір көпмүшелік, егер мұндай термин болса, формальды өрнекте қолданылған терминдердің қосындысына тең аменхмен барлық дәрежелерінде нөл коэффициенттері бар көпмүшелік ретінде түсіндіріледі х басқа хмен. Көбейтуді анықтау үшін, -ге жетеді тарату құқығы ереже бойынша берілген кез келген осындай екі терминнің көбейтіндісін сипаттау
- барлық элементтер үшін а, б сақина R және бәрі натурал сандар к және л.
Осылайша сақинадағы коэффициенттері бар барлық көпмүшеліктер жиыны R сақинаны құрайды көпмүшеліктер сақинасы аяқталды Rдеп белгіленеді R[х]. Картасы R дейін R[х] жіберіліп жатыр р дейін rx0 бұл сақиналардың инъекциялық гомоморфизмі R қосымшасы ретінде қарастырылады R[х]. Егер R болып табылады ауыстырмалы, содан кейін R[х] болып табылады алгебра аяқталды R.
Сақина туралы ойлауға болады R[х] ретінде пайда болады R бір жаңа элемент қосу арқылы х дейін Rжәне сақинаны минималды түрде созу х міндетті қатынастардан басқа қатынастарды қанағаттандырмайды, сонымен бірге барлық элементтерімен коммутация R (Бұл xr = rx). Ол үшін барлық күштерін қосу керек х және олардың сызықтық комбинациялары.
Факторинг арқылы фактор сақиналарын құрумен бірге полиномдық сақинаның түзілуі мұраттар, белгілі сақиналардан жаңа сақиналар салудың маңызды құралдары болып табылады. Мысалы, көпмүшелік сақинадан құрастыруға болатын күрделі сандардың сақинасы (шын мәнінде өрісі) R[х] көпмүшенің еселіктерінің идеалын көбейту арқылы нақты сандардың үстінен х2 + 1. Тағы бір мысал - ақырлы өрістер, ол кейбір модульдер бүтін сандар өрісінен басталып, ұқсас түрде жүреді жай сан коэффициент сақинасы ретінде R (қараңыз модульдік арифметика ).
Егер R коммутативті, онда кез келген көпмүшемен байланыстыруға болады P жылы R[х] а көпмүшелік функция f домен мен диапазонға тең R. (Жалпы алғанда, домен мен ауқымды кез келген бірдей етіп алуға болады біртұтас ассоциативті алгебра аяқталды R.) Біреуі құндылықты алады f(р) арқылы ауыстыру мәні р таңба үшін х жылы P. Көпмүшелер мен көпмүшелік функцияларды ажыратудың бір себебі мынада: кейбір сақиналардың үстінен әр түрлі көпмүшелер бірдей полиномдық функцияны туындатуы мүмкін (қараңыз) Ферманың кішкентай теоремасы мысалы қайда R бұл бүтін сандар модулі б). Бұл жағдайда емес R бұл нақты немесе күрделі сандар, мұнда екі ұғым әрқашан ерекшеленбейді талдау. Көпмүшеліктер мен көпмүшелік функцияларды ажыратудың маңызды себебі мынада: көпмүшеліктердегі көптеген амалдар (мысалы Евклидтік бөлім ) көпмүшені қандай-да бір тұрақты мәнде бағалағаннан гөрі, өрнек ретінде құрайтынын қарауды талап етеді х.
Бөлінгіштік
Жылы ауыстырмалы алгебра, зерттеудің басты бағыты бөлінгіштік көпмүшеліктер арасында. Егер R болып табылады интегралды домен және f және ж in көпмүшелері болып табылады R[х], дейді f бөледі ж немесе f бөлгіш болып табылады ж егер көпмүше болса q жылы R[х] осындай f q = ж. Әрбір нөл нөлдік сызықтық бөлгішке әкелетінін немесе егер формальды түрде формальды болатынын көрсетсе болады f in көпмүшесі болып табылады R[х] және р элементі болып табылады R осындай f(р) = 0, содан кейін көпмүшелік (х − р) бөледі f. Керісінше шындық. Келесі бөлімді есептеуге болады көпмүшелік ұзақ бөлу.[25][26]
Егер F Бұл өріс және f және ж in көпмүшелері болып табылады F[х] бірге ж ≠ 0, онда ерекше көпмүшелер бар q және р жылы F[х] бірге
және дәрежесі р дәрежесінен кіші ж (0 көпмүшесінің теріс дәрежесі бар деген шартты қолдану арқылы). Көпмүшелер q және р бірегей анықталады f және ж. Бұл деп аталады Евклидтік бөлім, қалдықпен бөлу немесе көпмүшелік ұзақ бөлу және сақина екенін көрсетеді F[х] Бұл Евклидтік домен.
Ұқсас, қарапайым көпмүшелер (дұрысырақ, қысқартылмайтын көпмүшелер ) ретінде анықтауға болады нөлге тең емес көпмүшелер, оларды екі тұрақты емес көпмүшенің көбейтіндісіне көбейту мүмкін емес. Сақинадағы коэффициенттер жағдайында, «тұрақты емес» ауыстырылуы керек «тұрақты емес немесе тұрақты емесбірлік " (өрістегі коэффициенттер жағдайында екі анықтама да сәйкес келеді). Кез-келген көпмүшені төмендетілмейтін полиномдар көбейтіндісі арқылы кері константаның көбейтіндісіне айналдыруға болады. Егер коэффициенттер өріске немесе а бірегей факторизация домені бұл ыдырау факторлардың ретіне және кез-келген бірлік емес факторды бірлікке көбейтуге дейін ерекше (және бірлік факторды бірдей бірлікке бөлу). Коэффициенттер бүтін сандарға, рационал сандарға немесе ақырлы өріске жататын болса, азаймайтындықты тексеру және факторизацияны азаймайтын полиномдарға есептеу алгоритмдері бар (қараңыз) Көпмүшелерді факторизациялау ). Бұл алгоритмдер қолмен есептеу үшін қолданылмайды, бірақ кез-келгенінде қол жетімді компьютерлік алгебра жүйесі. Эйзенштейн критерийі кейбір жағдайларда төмендетілмейтіндігін анықтау үшін қолдануға болады.
Позициялық белгілеу
Сияқты қазіргі позициялық сандар жүйелерінде ондық жүйе, цифрлар және олардың бүтін сандағы орналасуы, мысалы, 45, көпмүшенің стенографиялық жазбасы радикс немесе негіз, бұл жағдайда, 4 × 101 + 5 × 100. Басқа мысал ретінде, 5-радиусында 132 сияқты сандар тізбегі (ондық) санды білдіреді 1 × 52 + 3 × 51 + 2 × 50 = 42. Бұл ұсыныс ерекше. Келіңіздер б 1-ден үлкен натурал сан бол. Содан кейін әрбір натурал сан а түрінде ерекше түрде көрсетілуі мүмкін
қайда м теріс емес бүтін сан болып табылады және r 's - бүтін сандар
- 0 < рм < б және 0 ≤ рмен < б үшін мен = 0, 1, . . . , м − 1.[27]
Интерполяция және жуықтау
Полиномдық функциялардың қарапайым құрылымы оларды полиномдық жуықтамаларды қолдану арқылы жалпы функцияларды талдауда айтарлықтай пайдалы етеді. Жылы маңызды мысал есептеу болып табылады Тейлор теоремасы, бұл шамамен әрқайсысы дифференциалданатын функция жергілікті көпмүшелік функцияға ұқсайды, ал Стоун-Вейерштрасс теоремасы, бұл әрқайсысы үздіксіз функция бойынша анықталған ықшам аралық Нақты осьті бүкіл интервал бойынша көпмүшелік функциясы бойынша жуықтауға болады. Жақындаудың практикалық әдістеріне жатады көпмүшелік интерполяция және пайдалану сплайндар.[28]
Басқа қосымшалар
Полиномдар басқа объект туралы ақпаратты кодтау үшін жиі қолданылады. The тән көпмүшелік матрицаның немесе сызықтық оператордың операторы туралы ақпарат болады меншікті мәндер. The минималды көпмүшелік туралы алгебралық элемент сол элемент қанағаттандыратын ең қарапайым алгебралық қатынасты жазады. The хроматикалық көпмүше а график сол графиктің дұрыс бояуларының санын есептейді.
«Полином» термині, сын есім ретінде, көпмүшелік түрінде жазуға болатын шамалар немесе функциялар үшін де қолданыла алады. Мысалы, in есептеу күрделілігі теориясы фраза көпмүшелік уақыт аяқтауға кететін уақытты білдіреді алгоритм кіріс шамасы сияқты кейбір айнымалы полиномдық функциямен шектеледі.
Тарих
Determining the roots of polynomials, or "solving algebraic equations", is among the oldest problems in mathematics. However, the elegant and practical notation we use today only developed beginning in the 15th century. Before that, equations were written out in words. For example, an algebra problem from the Chinese Arithmetic in Nine Sections, circa 200 BCE, begins "Three sheafs of good crop, two sheafs of mediocre crop, and one sheaf of bad crop are sold for 29 dou." We would write 3х + 2ж + з = 29.
History of the notation
The earliest known use of the equal sign is in Роберт Рекорд Келіңіздер The Whetstone of Witte, 1557. The signs + for addition, − for subtraction, and the use of a letter for an unknown appear in Майкл Стифел Келіңіздер Arithemetica integra, 1544. Рене Декарт, жылы La géometrie, 1637, introduced the concept of the graph of a polynomial equation. He popularized the use of letters from the beginning of the alphabet to denote constants and letters from the end of the alphabet to denote variables, as can be seen above, in the general formula for a polynomial in one variable, where the а's denote constants and х denotes a variable. Descartes introduced the use of superscripts to denote exponents as well.[29]
Сондай-ақ қараңыз
- List of polynomial topics
- Көпмүшелік тізбек
- Polynomial transformation – Transformation of a polynomial induced by a transformation of its roots
- Polynomial mapping – Function such that the coordinates of the image of a point are polynomial functions of the coordinates of the point
Ескертулер
- ^ See "polynomial" and "binomial", Ағылшын тілінің ықшам сөздігі
- ^ «Математикалық рәміздер жинағы». Математикалық қойма. 2020-03-01. Алынған 2020-08-28.
- ^ а б Вайсштейн, Эрик В. "Polynomial". mathworld.wolfram.com. Алынған 2020-08-28.
- ^ а б "Polynomials | Brilliant Math & Science Wiki". brilliant.org. Алынған 2020-08-28.
- ^ а б c Barbeau, E.J. (2003). Көпмүшелер. Спрингер. 1-2 беттер. ISBN 978-0-387-40627-5.
- ^ Вайсштейн, Эрик В. "Zero Polynomial". MathWorld.
- ^ Edwards, Harold M. (1995). Сызықтық алгебра. Спрингер. б. 78. ISBN 978-0-8176-3731-6.
- ^ а б c Edwards, Harold M. (1995). Сызықтық алгебра. Спрингер. б. 47. ISBN 978-0-8176-3731-6.
- ^ Salomon, David (2006). Деректер мен компьютерлік байланыс үшін кодтау. Спрингер. б. 459. ISBN 978-0-387-23804-3.
- ^ а б Introduction to Algebra. Йель университетінің баспасы. 1965. б. 621.
Any two such polynomials can be added, subtracted, or multiplied. Furthermore , the result in each case is another polynomial
- ^ Kriete, Hartje (1998-05-20). Progress in Holomorphic Dynamics. CRC Press. б. 159. ISBN 978-0-582-32388-9.
This class of endomorphisms is closed under composition,
- ^ Marecek, Lynn; Mathis, Andrea Honeycutt (May 6, 2020). Intermediate Algebra 2e. Section 7.1: OpenStax.CS1 maint: орналасқан жері (сілтеме)
- ^ Haylock, Derek; Cockburn, Anne D. (2008-10-14). Understanding Mathematics for Young Children: A Guide for Foundation Stage and Lower Primary Teachers. SAGE. б. 49. ISBN 978-1-4462-0497-9.
We find that the set of integers is not closed under this operation of division.
- ^ а б Marecek, Lynn; Mathis, Andrea Honeycutt (May 6, 2020). Intermediate Algebra 2e. Section 5.4: OpenStax.CS1 maint: орналасқан жері (сілтеме)
- ^ Peter H. Selby, Steve Slavin, Practical Algebra: A Self-Teaching Guide, 2nd Edition, Вили, ISBN 0-471-53012-3 ISBN 978-0-471-53012-1
- ^ Вайсштейн, Эрик В. "Ruffini's Rule". mathworld.wolfram.com. Алынған 2020-07-25.
- ^ Barbeau, E.J. (2003). Көпмүшелер. Спрингер. pp. 80–2. ISBN 978-0-387-40627-5.
- ^ Barbeau, E.J. (2003). Көпмүшелер. Спрингер. pp. 64–5. ISBN 978-0-387-40627-5.
- ^ Proskuryakov, I.V. (1994). "Algebraic equation". Жылы Хазевинкель, Мичиел (ред.). Математика энциклопедиясы. т. 1. Springer. ISBN 978-1-55608-010-4.
- ^ Leung, Kam-tim; т.б. (1992). Polynomials and Equations. Гонконг университетінің баспасы. б. 134. ISBN 9789622092716.
- ^ McNamee, J.M. (2007). Numerical Methods for Roots of Polynomials, Part 1. Elsevier. ISBN 978-0-08-048947-6.
- ^ Powell, Michael J. D. (1981). Approximation Theory and Methods. Кембридж университетінің баспасы. ISBN 978-0-521-29514-7.
- ^ Gohberg, Israel; Lancaster, Peter; Rodman, Leiba (2009) [1982]. Matrix Polynomials. Classics in Applied Mathematics. 58. Lancaster, PA: Өнеркәсіптік және қолданбалы математика қоғамы. ISBN 978-0-89871-681-8. Zbl 1170.15300.
- ^ Horn & Johnson 1990, б. 36.
- ^ Irving, Ronald S. (2004). Integers, Polynomials, and Rings: A Course in Algebra. Спрингер. б. 129. ISBN 978-0-387-20172-6.
- ^ Jackson, Terrence H. (1995). From Polynomials to Sums of Squares. CRC Press. б. 143. ISBN 978-0-7503-0329-3.
- ^ Маккой (1968), б. 75)
- ^ de Villiers, Johann (2012). Mathematics of Approximation. Спрингер. ISBN 9789491216503.
- ^ Ховард Эвес, Математика тарихына кіріспе, Sixth Edition, Saunders, ISBN 0-03-029558-0
- ^ The coefficient of a term may be any number from a specified set. If that set is the set of real numbers, we speak of "polynomials over the reals". Other common kinds of polynomials are polynomials with integer coefficients, polynomials with complex coefficients, and polynomials with coefficients that are integers модуль кейбіреулері жай сан б.
- ^ This terminology dates from the time when the distinction was not clear between a polynomial and the function that it defines: a constant term and a constant polynomial define тұрақты функциялар.[дәйексөз қажет ]
- ^ In fact, as a біртектес функция, it is homogeneous of әрқайсысы дәрежесі.[дәйексөз қажет ]
- ^ Some authors use "monomial" to mean "моника monomial". See Knapp, Anthony W. (2007). Advanced Algebra: Along with a Companion Volume Basic Algebra. Спрингер. б. 457. ISBN 978-0-8176-4522-9.
- ^ This paragraph assumes that the polynomials have coefficients in a өріс.
Әдебиеттер тізімі
- Barbeau, E.J. (2003). Көпмүшелер. Спрингер. ISBN 978-0-387-40627-5.
- Bronstein, Manuel; және т.б., редакция. (2006). Solving Polynomial Equations: Foundations, Algorithms, and Applications. Спрингер. ISBN 978-3-540-27357-8.
- Кахен, Пол-Жан; Chabert, Jean-Luc (1997). Бүтін мәнді көпмүшелер. Американдық математикалық қоғам. ISBN 978-0-8218-0388-2.
- Ланг, Серж (2002), Алгебра, Математика бойынша магистратура мәтіндері, 211 (Үшінші ред. Қайта қаралды), Нью-Йорк: Springer-Verlag, ISBN 978-0-387-95385-4, МЫРЗА 1878556. This classical book covers most of the content of this article.
- Leung, Kam-tim; т.б. (1992). Polynomials and Equations. Гонконг университетінің баспасы. ISBN 9789622092716.
- Mayr, K. Über die Auflösung algebraischer Gleichungssysteme durch hypergeometrische Funktionen. Monatshefte für Mathematik und Physik т. 45, (1937) pp. 280–313.
- Маккой, Нил Х. (1968), Қазіргі алгебраға кіріспе, қайта қаралған басылым, Бостон: Эллин мен Бэкон, LCCN 68015225
- Prasolov, Victor V. (2005). Көпмүшелер. Спрингер. ISBN 978-3-642-04012-2.
- Sethuraman, B.A. (1997). "Polynomials". Rings, Fields, and Vector Spaces: An Introduction to Abstract Algebra Via Geometric Constructibility. Спрингер. ISBN 978-0-387-94848-5.
- Umemura, H. Solution of algebraic equations in terms of theta constants. In D. Mumford, Tata Lectures on Theta II, Progress in Mathematics 43, Birkhäuser, Boston, 1984.
- von Lindemann, F. Über die Auflösung der algebraischen Gleichungen durch transcendente Functionen. Nachrichten von der Königl. Gesellschaft der Wissenschaften, vol. 7, 1884. Polynomial solutions in terms of theta functions.
- von Lindemann, F. Über die Auflösung der algebraischen Gleichungen durch transcendente Functionen II. Nachrichten von der Königl. Gesellschaft der Wissenschaften und der Georg-Augusts-Universität zu Göttingen, 1892 edition.
Сыртқы сілтемелер
- "Polynomial", Математика энциклопедиясы, EMS Press, 2001 [1994]
- "Euler's Investigations on the Roots of Equations". Архивтелген түпнұсқа on September 24, 2012.





































![[-1,1]](https://wikimedia.org/api/rest_v1/media/math/render/svg/51e3b7f14a6f70e614728c583409a0b9a8b9de01)


















