Тангенциалды төртбұрыш - Tangential quadrilateral

Жылы Евклидтік геометрия, а тангенциалды төртбұрыш (кейде жай жанасушы төртбұрыш) немесе төртбұрыш Бұл дөңес төртбұрыш оның жақтары болуы мүмкін тангенс жалғызға шеңбер төртбұрыш ішінде. Бұл шеңбер деп аталады айналдыра Төртбұрыштың немесе іштей сызылған шеңбердің центрі ынталандыру және оның радиусы деп аталады инрадиус. Бұл төртбұрыштарды айналдыра немесе айналдыра айналдыра сызуға болатындықтан, оларды да атаған айналма төртбұрыштар, төртбұрышты айналдыру, және айналмалы төртбұрыштар.[1] Тангенциалды төртбұрыштар - бұл ерекше жағдай тангенциалды көпбұрыштар.
Төртбұрыштардың осы класы үшін жиі қолданылатын басқа атаулар жазылатын төртбұрыш, жазылмайтын төртбұрыш, жазылмайтын төртбұрыш, циклдік төртбұрыш, және коциклді төртбұрыш.[1][2] А деп аталатын дөңгелек шеңбері бар төртбұрышпен шатасу қаупіне байланысты циклдік төртбұрыш немесе төртбұрышпен жазылған болса, соңғы бес есімнің ешқайсысын қолданбаған жөн.[1]
Барлық үшбұрыштар айналдыра алады, бірақ төртбұрыштың бәрі бірдей бола бермейді. Тангенциалды бола алмайтын төртбұрыштың мысалы квадрат емес тіктөртбұрыш. Бөлім сипаттамалар төменде не жазылған қажетті және жеткілікті шарттар төртбұрыш айналдыра алу үшін қанағаттануы керек.
Ерекше жағдайлар
Тангенциалды төртбұрыштардың мысалдары: батпырауық қамтиды ромби, бұл өз кезегінде квадраттар. Батпырауықтар - бұл жанамалы төртбұрыштар ортодиагональды.[3] A оң жақ батпырауық а бар батпырауық шеңбер. Егер төртбұрыш жанама болса және циклдік, ол а деп аталады екі центрлік төртбұрыш, және егер ол тангенциалды және а трапеция, ол а деп аталады тангенциалды трапеция.
Мінездемелер
Тангенциалды төртбұрышта төртеу бұрыштық биссектрисалар шеңбердің ортасында кездеседі. Керісінше, төрт бұрыш биссектрисасы нүктеде түйісетін дөңес төртбұрыш жанамалы болуы керек, ал ортақ нүкте - қозғаушы.[4]
Сәйкес Питот теоремасы, тангенциалды төртбұрыштағы қарама-қарсы жақтардың екі жұбы бірдей жалпы ұзындыққа дейін қосылады, ол тең полимерметр с төртбұрыштың:
Керісінше, онда дөңес төртбұрыш а + c = б + г. тангенциалды болуы керек.[1]:65-бет[4]
Егер дөңес төртбұрышта қарама-қарсы жақтар болса А Б С Д (бұл а емес трапеция ) қиылысады E және F, содан кейін бұл тангенциалды егер және егер болса екінің бірі[4]
немесе
Бұлардың екіншісі - дегі теңдіктердің біріне ұқсас Уркхарт теоремасы. Жалғыз айырмашылық - екі жақтағы белгілер; Уркхарт теоремасында айырмашылықтардың орнына қосындылар бар.
Тағы бір қажетті және жеткілікті шарт - дөңес төртбұрыш А Б С Д тангенциалды, егер екі үшбұрыштағы шеңберлер болса ғана ABC және ADC болып табылады тангенс бір біріне.[1]:66-бет
Диагональмен құрылған бұрыштарға қатысты сипаттама BD және төртбұрыштың төрт жағы А Б С Д Иосифескуға байланысты. Ол 1954 жылы дөңес төртбұрыштың шеңбері болатынын дәлелдеді[5]
Әрі қарай, дәйекті жақтары бар дөңес төртбұрыш а, б, c, г. тангенциалды болып табылады және егер болса
қайда Rа, Rб, Rc, Rг. шеңберлерге сыртқы жанама радиустар болып табылады а, б, c, г. сәйкесінше және әр тарапқа іргелес екі жақтың кеңейтімдері.[6]:72-бет
Бірнеше басқа сипаттамалар диагональдары құрған төрт субтригенде белгілі.
Арнайы сызық сегменттері
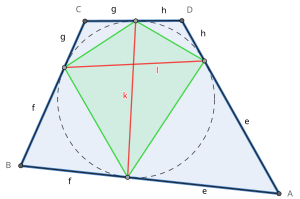
Сегіз жанама ұзындықтар (e, f, ж, сағ тангенциалдық төртбұрыштың оң жағындағы суретте а-дан түзілген кесінділер көрсетілген шың шеңбер шеңберге жанасатын нүктелерге дейін. Әр шыңнан екіден шығады үйлесімді жанама ұзындықтар.
Екі тангенстік аккордтар (к және л тангенциалды төртбұрыштың суретінде) шеңбер осы жақтарға жанасатын қарама-қарсы жақтағы нүктелерді қосатын сызық кесінділері. Бұл сондай-ақ диагональдар туралы контактілі төртбұрыш.
Аудан
Тригонометриялық емес формулалар
The аудан Қ тангенциалды төртбұрыштың мәні берілген
қайда с болып табылады полимерметр және р болып табылады инрадиус. Тағы бір формула - бұл[7]
бұл диагональ бойынша ауданды береді б, q және жақтары а, б, c, г. тангенциалды төртбұрыштың
Ауданды тек төртеуімен ғана көрсетуге болады жанама ұзындықтар. Егер бұл болса e, f, ж, сағ, сонда тангенциалды төртбұрыштың ауданы болады[3]
Сонымен қатар, тангенциалды төртбұрыштың ауданын жақтарымен өрнектеуге болады а б С Д жанама жанама ұзындықтар e, f, g, h сияқты[3]:128-бет
Бастап мысалы = fh егер тек тангенциалды төртбұрыш циклдік болса, демек, екі центрлік болса,[8] бұл максималды аудан екенін көрсетеді егер тангенциалды төртбұрыш екі центрлі болса ғана пайда болады.
Тригонометриялық формулалар
A тригонометриялық жағына қатысты ауданның формуласы а, б, c, г. және екі қарама-қарсы бұрыш[7][9][10][11]
Берілген бүйірлік ұзындықтар үшін аудан максимум төртбұрыш та болғанда циклдік және, демек, а екі центрлік төртбұрыш. Содан кейін өйткені қарама-қарсы бұрыштар қосымша бұрыштар. Мұны қолдану арқылы басқа жолмен дәлелдеуге болады есептеу.[12]
Тангенциалды төртбұрыш ауданының тағы бір формуласы А Б С Д екі қарама-қарсы бұрышты қамтитын болып табылады[10]:19 б
қайда Мен ынталандыру болып табылады.
Шындығында, ауданды тек екі іргелес жақтар және екі қарама-қарсы бұрыштар түрінде өрнектеуге болады[7]
Аймақтың тағы бір формуласы[7]
қайда θ диагональдар арасындағы бұрыштардың бірі болып табылады. Тангенциалдық төртбұрыш батпырауық болған кезде, бұл формуланы сол уақыттан бері қолдануға болмайды θ 90 °, ал тангенс функциясы анықталмаған.
Теңсіздіктер
Жоғарыда жанама түрде атап өткендей, жанама жанама төртбұрыштың ауданы а, б, c, г. қанағаттандырады
теңдікпен, егер ол а болған жағдайда ғана екі центрлік төртбұрыш.
Т.А.Иванованың айтуы бойынша (1976 ж.), Полимерметр с тангенциалды төртбұрышты қанағаттандырады
қайда р интрадиус болып табылады. Төртбұрыш а болған жағдайда ғана теңдік бар шаршы.[13] Бұл аймақ үшін дегенді білдіреді Қ = rs, бар теңсіздік
егер теңдеулі төртбұрыш квадрат болса ғана теңдікпен.
Бөлімнің қасиеттері

Айналаның центрі мен төртбұрышты төртбұрышқа жанама орналасқан нүктелер арасындағы төрт сызық сегменттері оң батпырауық.
Егер сызық тангенциалды төртбұрышты екіге бөлсе көпбұрыштар теңімен аудандар және тең периметрлер, содан кейін бұл сызық ынталандыру.[4]
Инрадиус
Қабырғалары қатарынан орналасқан тангенциалды төртбұрыштағы инрадиус а, б, c, г. арқылы беріледі[7]
қайда Қ төртбұрыштың және с бұл оның полиметрі. Қабырғалары берілген тангенциалды төртбұрыш үшін инрадиус мынаған тең максимум төртбұрыш та болғанда циклдік (демек, а екі центрлік төртбұрыш ).
Тұрғысынан жанама ұзындықтар, шеңбердің радиусы бар[8]:Лемма2[14]
Инрадиусты қоздырғыштан қашықтықта да көрсетуге болады Мен тангенциалды төртбұрыштың төбелеріне дейін А Б С Д. Егер u = AI, v = BI, x = CI және y = DI, содан кейін
қайда .[15]
Егер үшбұрыштардағы шеңберлер болса ABC, BCD, CDA, DAB радиустары бар сәйкесінше, содан кейін тангенциалды төртбұрыштың радиусы А Б С Д арқылы беріледі
қайда .[16]
Бұрыш формулалары
Егер e, f, ж және сағ болып табылады жанама ұзындықтар шыңдардан A, B, C және Д. сәйкесінше шеңбер шеңбері тангенциалды төртбұрыштың бүйірлеріне жанасатын нүктелерге А Б С Д, содан кейін бұрыштар төртбұрыштың мәнін есептеуге болады[3]
Арасындағы бұрыш тангенстік аккордтар к және л арқылы беріледі[3]
Диагональдар
Егер e, f, ж және сағ болып табылады жанама ұзындықтар бастап A, B, C және Д. сәйкесінше шеңбер шеңбері тангенциалды төртбұрыштың бүйірлеріне жанасатын нүктелерге А Б С Д, содан кейін диагональдардың ұзындықтары p = айнымалы ток және q = BD болып табылады[8]:Лемма3
Тангенстік аккордтар
Егер e, f, ж және сағ болып табылады жанама ұзындықтар тангенциалды төртбұрыштың, содан кейін тангенстік аккордтар болып табылады[3]
мұнда ұзындықтың тангенстік аккорды к ұзындықтардың бүйірлерін байланыстырады а = e + f және c = ж + сағжәне ұзындық л ұзындықтардың бүйірлерін байланыстырады б = f + ж және г. = сағ + e. Тангенстік аккордтардың квадраттық қатынасы қанағаттандырады[3]
Екі тангенстік аккордтар
- болып табылады перпендикуляр егер тек қана тангенциалдық төртбұрышта a бар болса ғана шеңбер (Бұл бицентрлік ).[3]:124-бет
- тангенциалдық төртбұрыш а болған жағдайда ғана бірдей ұзындықтарға ие болыңыз батпырауық.[17]:166-бет
Тараптар арасындағы жанасу аккорды AB және CD тангенциалды төртбұрышта А Б С Д жақтардың арасына қарағанда ұзын Б.з.д. және DA егер және егер болса бимедия жақтардың арасында AB және CD жақтардың арасына қарағанда қысқа Б.з.д. және DA.[18]:162-бет
Егер тангенциалды төртбұрыш А Б С Д жанасу нүктелері бар W қосулы AB және Y қосулы CDжәне егер тангент аккорды болса WY диагональмен қиылысады BD кезінде М, содан кейін жанама ұзындықтардың қатынасы қатынасына тең диагональ сегменттерінің BD.[19]
Сызықтық нүктелер
Егер М1 және М2 болып табылады ортаңғы нүктелер диагональдардың Айнымалы және BD сәйкесінше тангенциалды төртбұрышта А Б С Д ынталандыру арқылы Мен, және егер қарама-қарсы жақтардың жұптары кездесе қалса Дж және Қ бірге М3 ортаңғы нүктесі болу JK, содан кейін ұпайлар М3, М1, Мен, және М2 болып табылады коллинеарлы.[4]:42-бет Оларды қамтитын жол - Ньютон сызығы төртбұрыштың
Егер тангенциалды төртбұрыштағы қарама-қарсы жақтардың кеңеюі -мен қиылысса Дж және Қ, және оның жанасу төртбұрышындағы қарама-қарсы жақтардың кеңеюі -мен қиылысады L және М, содан кейін төрт ұпай Дж, L, Қ және М коллинеарлы.[20]:Кор.3
Егер айналдыра жанама болса AB, Б.з.д., CD, DA кезінде Т1, Т2, Т3, Т4 сәйкесінше, және егер N1, N2, N3, N4 болып табылады изотомдық конъюгаттар осы тармақтардың сәйкес жақтарына қатысты (яғни, AT1 = BN1 және т.б.), содан кейін Нагель нүктесі тангенциалды төртбұрыштың түзулердің қиылысы ретінде анықталады N1N3 және N2N4. Бұл екі жол да периметрі төртбұрышты екі тең бөлікке бөлу. Ең бастысы, Нагель нүктесі N, «аймақтық центроид» Gжәне ынталандыру Мен осы тәртіпте коллинеар болып табылады және NG = 2GI. Бұл жол деп аталады Нагель сызығы тангенциалды төртбұрыштың[21]
Тангенциалды төртбұрышта А Б С Д ынталандыру арқылы Мен және диагональдар қиылысатын жерде P, рұқсат етіңіз HX, HY, HЗ, HW болуы ортоцентрлер үшбұрыштар AIB, BIC, CID, ІІД. Содан кейін ұпайлар P, HX, HY, HЗ, HW коллинеарлы.[10]:28-бет
Параллель және перпендикуляр түзулер
Екі диагональ және екі тангенстік аккордтар қатарлас.[11][10]:11-бет Мұны көрудің бір жолы - бұл шектеулі жағдай Бриансон теоремасы, онда алтыбұрыш, оның барлық жағы жалғызға жанама екендігі айтылады конустық бөлім нүктесінде түйісетін үш диагоналы бар. Тангенциалды төртбұрыштан екі жанама шыңдарды жанасу нүктелеріне қарама-қарсы қою арқылы екі 180 ° бұрыштары бар алтыбұрышты құруға болады; осы алтыбұрыштың барлық алты қабырғасы сызылған шеңберге жанама сызықтарда жатыр, сондықтан оның диагональдары бір нүктеде түйіседі. Бірақ бұл диагональдардың екеуі тангенциалды төртбұрыштың диагональдарымен бірдей, ал алтыбұрыштың үшінші диагоналы - бұл жанама екі қарама-қарсы жанама нүктелер арқылы өтетін сызық. Дәл осы аргументті тангенстің қалған екі нүктесімен қайталау нәтиженің дәлелденуін аяқтайды.
Егер тангенциалды төртбұрыштағы қарама-қарсы жақтардың кеңеюі -мен қиылысса Дж және Қ, және диагональдар қиылысады P, содан кейін JK кеңейтуіне перпендикуляр IP қайда Мен ынталандыру болып табылады.[20]:Кор.4
Инцентр
Тангенциалды төртбұрыштың қозғаушы күші осыған негізделген Ньютон сызығы (бұл диагональдардың ортаңғы нүктелерін қосады).[22]:Thm. 3
Тангенциалдық төртбұрыштағы екі қарама-қарсы жақтың қатынасын ынталандыру арасындағы қашықтықта көрсетуге болады Мен және сәйкесінше шыңдар[10]:15 б
Тангенциалды төртбұрыштағы көршілес екі жақтың көбейтіндісі А Б С Д ынталандыру арқылы Мен қанағаттандырады[23]
Егер Мен тангенциалды төртбұрыштың қозғаушысы А Б С Д, содан кейін[10]:16-бет
Ынталандыру Мен тангенциалды төртбұрышта А Б С Д сәйкес келеді «шыңы центроид» төртбұрыштың егер және егер болса[10]:22-бет
Егер Мб және Мq болып табылады ортаңғы нүктелер диагональдардың Айнымалы және BD сәйкесінше тангенциалды төртбұрышта А Б С Д ынталандыру арқылы Мен, содан кейін [10]:19 б[24]
қайда e, f, ж және сағ жанама ұзындықтар A, B, C және Д. сәйкесінше. Бірінші теңдікті алдыңғы қасиетпен біріктіре отырып, тангенциалды төртбұрыштың «шың центройы» қоздырғышпен сәйкес келеді, егер қозғаушы диагональдардың ортаңғы нүктелерін қосатын сызық сегментінің орта нүктесі болса.
Егер а төрт жолақты байланыс тангенциалды төртбұрыш түрінде жасалады, егер ол төртбұрыш дөңес болып қалса, байланыс қалайша иілсе де, тангенциалды болып қалады.[25][26] (Мәселен, мысалы, егер квадрат ромбқа айналса, ол кіші шеңберге дейін жанамалы болып қалады). Егер бір жағы бекітілген күйде ұсталса, онда төртбұрыш бүгілген кезде қоздырғыш радиустың шеңберін шығарады қайда а б С Д және кезектегі жақтар болып табылады с - бұл полиметр.
Төрт субтригендегі сипаттамалар

Қабаттаспайтын үшбұрыштарда APB, BPC, CPD, DPA дөңес төртбұрышта диагональдармен түзілген А Б С Д, онда диагональдар қиылысады P, тангенциалды төртбұрыштардың келесі сипаттамалары бар.
Келіңіздер р1, р2, р3, және р4 төрт үшбұрыштағы шеңберлердің радиустарын белгілеңіз APB, BPC, CPD, және DPA сәйкесінше. Чао мен Симеонов төртбұрыштың тангенциалды екенін дәлелдеді егер және егер болса[27]
Бұл сипаттаманы бес жыл бұрын Вайнштейн дәлелдеген болатын.[17]:169-бет[28]Оның мәселесін шешуде Васильев пен Сендеров осындай сипаттама берген. Егер сағ1, сағ2, сағ3, және сағ4 белгілеу биіктік сол төрт үшбұрышта (диагональды қиылысудан төртбұрыштың бүйірлеріне дейін), онда төртбұрыш тангенциалды болады, егер[5][28]
Осындай сипаттаманың тағы біреуі exradii ра, рб, рc, және рг. сол төрт үшбұрышта (төртеу шеңберлер әрқайсысы төртбұрыштың бір жағына және оның диагональдарының кеңеюіне тең). Төртбұрыш тангенциалды болады, егер болса және ол[1]:70-бет
Егер R1, R2, R3, және R4 радиустарын шеңберлер үшбұрыштар APB, BPC, CPD, және DPA сәйкесінше, содан кейін төртбұрыш А Б С Д тангенциалды болып табылады және егер болса[29]:23-24 бет
1996 жылы Вайнштейн алғашқы тангенс төртбұрыштарының сипаттамаларын бірінші болып дәлелдеді, кейінірек бірнеше журналдарда және сайттарда пайда болды.[1]:72-73 бет Онда дөңес төртбұрышты екі диагональ бойынша бір-біріне жабыспайтын төртбұрышқа бөлгенде, төртбұрыш тангенциалды болған жағдайда ғана төрт үшбұрыштың қозғалғыштары консиклді болады деп айтылады. Шын мәнінде, ынталандырулар ан ортадиагональды циклді төртбұрыш.[1]:74-бет Осыған байланысты нәтиже шеңберлерді бірдей үшбұрыштардың шеңберлерімен алмастыруға болады (төртбұрыштың бүйірлеріне жанама және оның диагональдарының кеңеюі). Осылайша, дөңес төртбұрыш тек осы төртеудегі экцентрлер болған жағдайда ғана тангенциалды болады шеңберлер а шыңдары болып табылады циклдік төртбұрыш.[1]:б. 73
Дөңес төртбұрыш А Б С Д, қиылысатын диагональдармен P, егер үшбұрыштағы төрт көтергіш болса ғана, тангенциалды болады APB, BPC, CPD, және DPA шыңдарға қарама-қарсы B және Д. конциклді болып табылады.[1]:б. 79 Егер Rа, Rб, Rc, және Rг. үшбұрыштардағы экстради болып табылады APB, BPC, CPD, және DPA сәйкесінше шыңдарға қарама-қарсы B және Д., онда тағы бір шарт - төртбұрыш тангенциалды, егер ол болса ғана[1]:б. 80
Әрі қарай, дөңес төртбұрыш А Б С Д қиылысатын қиғаштармен P тангенциалды болып табылады және егер болса[5]
қайда ∆ (APB) - бұл үшбұрыштың ауданы APB.
Диагональды қиылысатын кесінділерді белгілеңіз P диагональды бөледі Айнымалы ретінде AP = б1 және ДК = б2, және сол сияқты P диагональды бөледі BD сегменттерге бөлу BP = q1 және PD = q2. Төмендегі теңдіктердің кез-келгені дұрыс болған жағдайда ғана төртбұрыш тангенциалды болады:[30]
немесе[1]:б. 74
немесе[1]:б. 77
Тангенциалды төртбұрыштың төртбұрыштың басқа түрі болу шарттары
Ромб
Тангенциалды төртбұрыш - а ромб егер оның қарама-қарсы бұрыштары тең болса ғана.[31]
Батпырауық
Тангенциалды төртбұрыш - а батпырауық егер келесі шарттардың кез-келгені дұрыс болса ғана:[17]
- Аудан өнімнің жартысына тең диагональдар.
- Қиғаштар перпендикуляр.
- Тангенстің қарама-қарсы нүктелерін қосатын екі сызық сегменттерінің ұзындығы тең.
- Бір жұп қарама-қарсы жанама ұзындықтар тең ұзындыққа ие
- The бимедиялар тең ұзындыққа ие
- Қарама-қарсы жақтардың көбейтінділері тең.
- Айналдырудың центрі симметрия осі болып табылатын диагональда жатыр.
Екіцентрлік төртбұрыш
Егер айналдыра жанама болса AB, Б.з.д., CD, DA кезінде W, X, Y, З тиісінше, содан кейін тангенциалды төртбұрыш А Б С Д сонымен қатар циклдік (демек, бицентрлік ) егер келесі шарттардың кез-келгені болса ғана:[2][3]:124-бет[20]
- WY перпендикуляр XZ
Осы үшеудің біріншісі - дегенді білдіреді контактілі төртбұрыш WXYZ болып табылады ортадиагоналды төртбұрыш.
Тангенциалды төртбұрыш, егер оның радиусы бүйірлік ұзындықтары бірдей кез келген басқа тангенциалдық төртбұрышқа қарағанда үлкен болса ғана, екі центрлік болады.[32]:392-339 бб
Тангенциалды трапеция
Егер айналдыра жанама болса AB және CD кезінде W және Y тиісінше, содан кейін тангенциалды төртбұрыш А Б С Д сонымен қатар трапеция параллель жақтары бар AB және CD егер және егер болса[33]:Thm. 2018-04-21 121 2
және AD және Б.з.д. егер болған жағдайда ғана трапецияның параллель жақтары болып табылады
Сондай-ақ қараңыз
Әдебиеттер тізімі
- ^ а б c г. e f ж сағ мен j к л м Джозефссон, Мартин (2011), «Тангенциалдық төртбұрыштардың қосымша сипаттамалары» (PDF), Форум Geometricorum, 11: 65–82.
- ^ а б Брайант, Виктор; Дункан, Джон (2010), «Дөңгелектер ішіндегі дөңгелектер», Математикалық газет, 94 (Қараша): 502–505.
- ^ а б c г. e f ж сағ мен Джозефссон, Мартин (2010), «Тангенциалды төртбұрыштың жанама ұзындықтары мен тангенстік аккордтарына қатысты есептеулер» (PDF), Форум Geometricorum, 10: 119–130.
- ^ а б c г. e Андреску, Титу; Энеску, Богдан (2006), Математикалық олимпиада қазыналары, Бирхязер, 64-68 бет.
- ^ а б c Минкулете, Никусор (2009), «Тангенциалды төртбұрыштың сипаттамалары» (PDF), Форум Geometricorum, 9: 113–118.
- ^ Джозефссон, Мартин (2012), «Тангенциалды және эксангенциалды төртбұрыштардың ұқсас метрикалық сипаттамалары» (PDF), Форум Geometricorum, 12: 63–77
- ^ а б c г. e Дюрелл, КВ .; Робсон, А. (2003), Жетілдірілген тригонометрия, Доверді қайта басу, 28-30 б.
- ^ а б c Хаджа, Моваффак (2008), «Айналмалы төртбұрыштың циклді болу шарты» (PDF), Форум Geometricorum, 8: 103–106.
- ^ Сиддонс, А.В .; Хьюз, Р.Т. (1929), Тригонометрия, Кембридж Университеті. Түймесін басыңыз, б. 203.
- ^ а б c г. e f ж сағ Гринберг, Даридж, Шектелген төртбұрыштар қайта қаралды, 2008
- ^ а б Иу, Пол, Евклидтік геометрия, [1], 1998, 156–157 б.
- ^ Хойт, Джон П. (1986), «Трапеция аумағын максимизациялау», Американдық математикалық айлық, 93 (1): 54–56, дои:10.2307/2322549.
- ^ Хабарлама Мәселелерді шешу өнері, 2012
- ^ Хойт, Джон П. (1984), «Quickies, Q694», Математика журналы, 57 (4): 239, 242.
- ^ Джозефссон, Мартин (2010), «Тангенциалды төртбұрыштың радиусында» (PDF), Форум Geometricorum, 10: 27–34.
- ^ Богомольный, Александр (2016), жазылмайтын төртбұрыштағы инрадиялық қатынас, Түйін, [2].
- ^ а б c Джозефссон, Мартин (2011), «Тангенциалды төртбұрыш қашан батпырауық болады?» (PDF), Форум Geometricorum, 11: 165–174.
- ^ Джозефссон, Мартин (2011), «Екіцентрлік төртбұрыштың ауданы» (PDF), Форум Geometricorum, 11: 155–164.
- ^ Гутиеррес, Антонио, «Айналдырылған төртбұрыш, диагональ, аккорд, пропорция», [3], Қол жеткізілді 2012-04-09.
- ^ а б c Джозефссон, Мартин (2010), «Екіцентрлік төртбұрыштардың сипаттамалары» (PDF), Форум Geometricorum, 10: 165–173.
- ^ Мякишев, Алексей (2006), «Төртбұрышқа қатысты екі керемет сызық туралы» (PDF), Форум Geometricorum, 6: 289–295.
- ^ Дергиадес, Николаос; Кристодулу, Димитрис М. (2017), «Ерікті дөңес төртбұрыштың екі ынтасы» (PDF), Форум Geometricorum, 17: 245–254.
- ^ «Ineq-G126 - Геометрия - өте жақсы !!!!», Post at Мәселелерді шешу өнері, 2011, [4]
- ^ «OM / ON қатынасын анықтаңыз», Post at Мәселелерді шешу өнері, 2011
- ^ Бартон, Хелен (1926), «Жиналмалы төрт барға бекітілген шеңберде», Американдық математикалық айлық, 33 (9): 462–465, дои:10.2307/2299611, JSTOR 2299611.
- ^ Богомольный, Александр, «Төртбұрыш жазылмаған кезде?», Интерактивті математика Әр түрлі және басқатырғыштар, [5].
- ^ Чао, Ву Вэй; Симеонов, Пламен (2000), «Төртбұрыштар шеңбер жазған кезде (10698 есебінің шешімі)», Американдық математикалық айлық, 107 (7): 657–658, дои:10.2307/2589133.
- ^ а б Вайнштейн, Мен .; Васильев, Н .; Сендеров, В. (1995), «(Шешім шешімі) M1495», Квант (6): 27–28.
- ^ Джозефссон, Мартин (2012), «Ортиагоналды төртбұрыштардың сипаттамалары» (PDF), Форум Geometricorum, 12: 13–25.
- ^ Хон, Ларри (2011), «Төртбұрыштың диагональдары мен қабырғаларына қатысты жаңа формула» (PDF), Форум Geometricorum, 11: 211–212.
- ^ Де Виллиерс, Майкл (2011), «Екібұрышты циклді және тең бүйірлі айналма полигондар», Математикалық газет, 95 (Наурыз): 102–107.
- ^ Гесс, Альбрехт (2014), «Тангенциалды төртбұрыштардың қозғалғыштары бар шеңберде» (PDF), Форум Geometricorum, 14: 389–396.
- ^ Джозефссон, Мартин (2014), «Диагональды нүктелік үшбұрыш қайта қаралды» (PDF), Форум Geometricorum, 14: 381–385.
























































