Тұрақты карта (график теориясы) - Regular map (graph theory)

Жылы математика, а тұрақты карта симметриялы болып табылады тесселляция жабық беті. Дәлірек айтсақ, кәдімгі карта - а ыдырау екі өлшемді көпжақты (мысалы сфера, торус, немесе нақты проективті жазықтық топологиялық дискілерге жалау (инциденттің шыңы-шеті-үштік инцидент) кез келген басқа жалаушаға айналуы мүмкін симметрия ыдырау Тұрақты карталар белгілі бір мағынада топологиялық жалпылау болып табылады Платондық қатты денелер. Карталар теориясы және олардың классификациясы теориясымен байланысты Риманның беттері, гиперболалық геометрия, және Галуа теориясы. Кәдімгі карталар екіге сәйкес жіктеледі: түр және бағдарлық тіреу бетінің, негізгі график немесе автоморфизм тобы.
Шолу
Тұрақты карталар әдетте үш жолмен анықталады және зерттеледі: топологиялық, топтық-теориялық және графикалық-теориялық.
Топологиялық тәсіл
Топологиялық тұрғыдан карта - бұл а 2-ұяшық жабық ықшам 2-коллектордың ыдырауы.
M картасының g, тегі берілген Эйлер қатынасы тең егер карта бағдарланған болса, және егер карта бағдарланбаған болса. Тордан басқа бағдарланған барлық тұқымдастар үшін тұрақты карталардың ақырғы (нөлдік емес) саны бар екендігі өте маңызды.
Топтық-теориялық тәсіл
Топтық-теориялық тұрғыдан тұрақты картаның орнын ауыстыру көрінісі М өтпелі болып табылады ауыстыру тобы C, жиынтықта туралы жалаушалар, үш тұрақты нүкте арқылы жасалады р0, р1, р2 қанағаттанарлық (р0р2)2= I. Бұл анықтамада беттер орбиталары болып табылады F = <р0, р1>, жиектері - орбиталары E = <р0, р2>, ал шыңдар - орбиталары V = <р1, р2>. Неғұрлым абстрактілі түрде кез-келген тұрақты картаның автоморфизм тобы дегеніміз a <2, m, n> - деградацияланбаған, гомоморфты кескін.үшбұрыш тобы.
Графикалық-теориялық тәсіл
Графикалық-теориялық тұрғыдан карта - текше граф көк, сары, қызыл түстермен: қосылған, әр шың әр түстің бір шетіне түседі, ал сары түске боялмаған жиектер циклдарының ұзындығы 4 болады. болып табылады жалауша сызбасы немесе графикалық кодталған карта (GEM) жалаулардың шыңында анықталған картаның және картаның G = (V, E) қаңқасы емес. Жалпы, || = 4 | E |.
M картасы тұрақты болып табылады, егер Aut (M) әрекет етеді үнемі жалауларда. Авт. (М) тұрақты картаның шыңдарында, шеттерінде және беттерінде өтпелі болып табыладыМ. Карта М егер Aut Aut икемді (М) тұрақты және құрамында автоморфизм бар ол шыңды да бекітедіv және бетf, бірақ жиектердің ретін өзгертеді. Қарта тұрақты, бірақ икемді емес деп аталады хирал.
Мысалдар

- The керемет додекаэдр бұл 4-тің бағдарланған бетінде бесбұрышты беткейлері бар тұрақты карта.
- The гемикуб ішіндегі {4,3} типті тұрақты карта проективті жазықтық.
- The жарты-додекаэдр бұл проекциялық жазықтықта Петерсен графигін бесбұрышты енгізу арқылы жасалған тұрақты карта.
- P-hosohedron {2, p} типті тұрақты карта.
- The Дайк картасы - бұл 3 тұқымдас бетіндегі 12 сегізбұрыштың тұрақты картасы. Оның астындағы график Дайк графигі, сонымен қатар торуста 16 алтыбұрыштың тұрақты картасын құра алады.
Төменде позитивті беттердегі тұрақты карталардың толық тізімі келтірілген Эйлерге тән, χ: сфера және проективті жазықтық.[1]
| χ | ж | Шлафли | Vert. | Шеттер | Жүздер | Топ | Тапсырыс | График | Ескертулер | |
|---|---|---|---|---|---|---|---|---|---|---|
| 2 | 0 | {б, 2} | б | б | 2 | C2 × Дихб | 4б | Cб | Диедрон | |
| 2 | 0 | {2, б} | 2 | б | б | C2 × Дихб | 4б | б-қатысу Қ2 | Хоседр | |
| 2 | 0 | {3,3} | 4 | 6 | 4 | S4 | 24 | Қ4 | Тетраэдр | |
| 2 | 0 | {4,3} | 8 | 12 | 6 | C2 × S4 | 48 | Қ4 × Қ2 | Текше | |
| 2 | 0 | {3,4} | 6 | 12 | 8 | C2 × S4 | 48 | Қ2,2,2 | Октаэдр | |
| 2 | 0 | {5,3} | 20 | 30 | 12 | C2 × A5 | 120 | Додекаэдр | ||
| 2 | 0 | {3,5} | 12 | 30 | 20 | C2 × A5 | 120 | Қ6 × Қ2 | Икозаэдр | |
| 1 | n1 | {2б, 2} / 2 | б | б | 1 | Дих2б | 4б | Cб | Жартылай диедрон[2] | |
| 1 | n1 | {2,2p} / 2 | 2 | б | б | Дих2б | 4б | б-қатысу Қ2 | Хеми-хозедр[2] | |
| 1 | n1 | {4,3}/2 | 4 | 6 | 3 | S4 | 24 | Қ4 | Гемикуб | |
| 1 | n1 | {3,4}/2 | 3 | 6 | 4 | S4 | 24 | 2 есе Қ3 | Гемиоктаэдр | |
| 1 | n1 | {5,3}/2 | 10 | 15 | 6 | A5 | 60 | Питерсен графигі | Гемидодекаэдр | |
| 1 | n1 | {3,5}/2 | 6 | 15 | 10 | A5 | 60 | Қ6 | Геми-икосаэдр | |
Төмендегі суреттердегі 20 тұрақты картаның үшеуі көрсетілген үштік тор, олармен белгіленген Schläfli таңбалары.
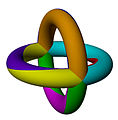
{6,4}

{4,8}

{8,4}
Тороидтық полиэдра
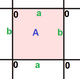 {4,4}1,0 (v: 1, e: 2, f: 1) | 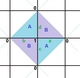 {4,4}1,1 (v: 2, e: 4, f: 2) | 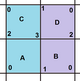 {4,4}2,0 (v: 4, e: 8, f: 4) |  {4,4}2,1 (v: 5, e: 10, f: 5) | 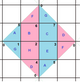 {4,4}2,2 (v: 8, e: 16, f: 8) |
 {3,6}1,0 (v: 1, e: 3, f: 2) | 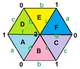 {3,6}1,1 (v: 3, e: 9, f: 6) | 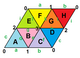 {3,6}2,0 (v: 4, e: 8, f: 8) | {3,6}2,1 (v: 7, e: 21, f: 14) |  {3,6}2,2 (v: 12, e: 36, f: 24) |
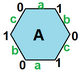 {6,3}1,0 (v: 2, e: 3, f: 1) |  {6,3}1,1 (v: 6, e: 9, f: 3) |  {6,3}2,0 (v: 8, e: 8, f: 4) |  {6,3}2,1 (v: 14, e: 21, f: 7) |  {6,3}2,2 (v: 24, e: 36, f: 12) |
Кәдімгі карталар беткі қабатына оралған евклидті плиткалардың ақырғы бөліктері сияқты, торедрлік полиэдра түрінде болады. дуоцилиндр сияқты жалпақ тор. Олар {4,4} деп белгіленгенб,c байланысты шаршы плитка, {4,4}.[3] {3,6}б,c байланысты үшбұрышты плитка, {3,6} және {6,3}б,c байланысты алты бұрышты плитка, {6,3}. б және c болып табылады бүтін сандар.[4] 2 ерекше жағдай бар (б, 0) және (б,б) шағылысатын симметриямен, ал жалпы жағдайлар хираль жұптарында болады (б,c) және (c,б).
{4,4} формасының тұрақты карталарым,0 ақырлы ретінде ұсынылуы мүмкін кәдімгі қиғаш полиэдр {4,4 | м}, а-ның квадрат беттері ретінде көрінеді м×м дуопризм 4 өлшемді.
Мысал {4,4}8,0 а ретінде жазықтықта бейнеленген шахмат тақтасы цилиндр бөліміне торусқа дейін. Цилиндрден торусқа дейінгі проекция геометрияны 3 өлшемде бұрмалайды, бірақ 4 өлшемде бұрмалаусыз жасауға болады.

| χ | ж | Шлафли | Vert. | Шеттер | Жүздер | Топ | Тапсырыс | Ескертулер |
|---|---|---|---|---|---|---|---|---|
| 0 | 1 | {4,4}б,0 n=б2 | n | 2n | n | [4,4](б,0) | 8n | Тегіс тороидты полиэдра {4,4 | сияқты б} |
| 0 | 1 | {4,4}б,б n=2б2 | n | 2n | n | [4,4](б,б) | 8n | Тегіс тороидты полиэдра Ректирленген {4,4 | сияқты б} |
| 0 | 1 | {4,4}б,c n=б2+c2 | n | 2n | n | [4,4]+ (б,c) | 4n | Тегіс хиральды тороидты полиэдра |
| 0 | 1 | {3,6}б,0 т=б2 | т | 3т | 2т | [3,6](б,0) | 12т | Тегіс тороидтық полиэдра |
| 0 | 1 | {3,6}б,б т=2б2 | т | 3т | 2т | [3,6](б,б) | 12т | Тегіс тороидты полиэдра |
| 0 | 1 | {3,6}б,c т=б2+б.з.д.+c2 | т | 3т | 2т | [3,6]+ (б,c) | 6т | Тегіс хиральды тороидты полиэдра |
| 0 | 1 | {6,3}б,0 т=б2 | 2т | 3т | т | [3,6](б,0) | 12т | Тегіс тороидты полиэдра |
| 0 | 1 | {6,3}б,б т=2б2 | 2т | 3т | т | [3,6](б,б) | 12т | Тегіс тороидты полиэдра |
| 0 | 1 | {6,3}б,c т=б2+б.з.д.+c2 | 2т | 3т | т | [3,6]+ (б,c) | 6т | Тегіс хиральды тороидты полиэдра |
Жалпы тороидальды полиэдрада {б,q}б,c егер болса, анықтауға болады б немесе q біркелкі, дегенмен жоғарыда тек эвклидтіктер 4 өлшемді тороидальды полиэдра ретінде өмір сүре алады. {2б,q}, жолдар (б,c) түзу сызықтармен беткейлік-беткейлік қадам ретінде анықталуы мүмкін, ал қосарланған {б,2q} пішіндер жолдарды көреді (б,c) түзу сызықтардағы шың-шеті-шыңы ретінде.
Сондай-ақ қараңыз
- Топологиялық графикалық теория
- Абстрактілі политоп
- Пландық график
- Тороидтық график
- Графикалық ендіру
- Үнемі плитка төсеу
- Платондық қатты зат
- Платондық график
Әдебиеттер тізімі
- ^ Коксетер (1980)
- ^ а б Секвин, Карло. «Бағытталмаған тұрақты карталардың симметриялы батырылуы» (PDF). Беркли университеті.
- ^ Коксетер 1980, 8.3 Торастағы {4,4} типті карталар.
- ^ Коксетер 1980, 8.4 Торастағы {3,6} немесе {6,3} типті карталар.
- ^ Коксетер және Мозер, Дискретті топтар үшін генераторлар мен қатынастар1957 ж., 8 тарау, Кәдімгі карталар, 8.3 Торуста {4,4} типті карталар, 8.4 Тораста {3,6} немесе {6,3} типті карталар
- Коксетер, H. S. M.; Мозер, W. O. J. (1980), Дискретті топтар үшін генераторлар мен қатынастар, Ergebnisse der Mathematik und ihrer Grenzgebiete, 14 (4-ші басылым), Springer Verlag, ISBN 978-0-387-09212-6.
- ван Вайк, Джарке Дж. (2009), «Жабық беттерге симметриялық плитка салу: тұрақты карталарды визуализациялау» (PDF), Proc. СИГРАФ (Графика бойынша ACM транзакциялары), 28 (3): 12, дои:10.1145/1531326.1531355, мұрағатталған түпнұсқа (PDF ) 2011-06-09.
- Кондер, Марстон; Добчании, Питер (2001), «Шағын тұқымдастардың барлық тұрақты карталарын анықтау», Комбинаторлық теория журналы, В сериясы, 81 (2): 224–242, дои:10.1006 / jctb.2000.2008.
- Недела, Роман (2007), Карталар, гипермарталар және басқа тақырыптар (PDF).
- Винс, Эндрю (2004), «Карталар», Графикалық теорияның анықтамалығы.
- Брем, Ульрих; Шульте, Эгон (2004), «Полиэдралды карталар», Дискретті және есептеу геометриясының анықтамалығы.










