Langleys адвентитивті бұрыштары - Langleys Adventitious Angles - Wikipedia

Лэнглидің адвенттік бұрыштары математикалық есеп болып табылады Эдвард Манн Лэнгли жылы Математикалық газет 1922 ж.[1][2]
Мәселесі
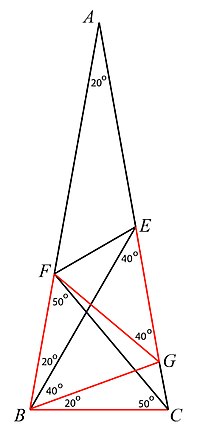
Мәселе өзінің бастапқы түрінде келесідей болды:
- болып табылады тең бүйірлі үшбұрыш.
- кезінде дейін кесу жылы
- кезінде дейін кесу жылы
Шешім
Шешімін әзірледі Джеймс Мерсер 1923 ж.[2] Бұл шешімге қосымша бір сызық сызу, содан кейін үшбұрыштың ішкі бұрыштарының 180 ° дейін қосылуын бірнеше рет пайдаланып, үлкен үшбұрыштың ішіне сызылған бірнеше үшбұрыштардың барлығы тең қабырғалы екенін дәлелдеу керек.
- Сурет салу кезінде дейін қиылысу кезінде және сурет салыңыз (Төменгі оң жақтағы суретті қараңыз.)
- Бастап және содан кейін және үшбұрыш тең бүйірлі болып табылады
- Бастап және содан кейін және үшбұрыш тең бүйірлі болып табылады
- Бастап және содан кейін үшбұрыш болып табылады тең жақты.
- Бастап және содан кейін және үшбұрыш тең бүйірлі болып табылады
- Сондықтан суреттегі барлық қызыл сызықтар тең.
- Бастап үшбұрыш тең бүйірлі болып табылады
- Сондықтан
Көптеген басқа шешімдер мүмкін. Түйіндер тізімін бірдей 80-80-20 үшбұрышымен, бірақ ішкі бұрыштары әр түрлі он екі шешімді және бірнеше балама есептерді қиып алыңыз.[4]
Жалпылау
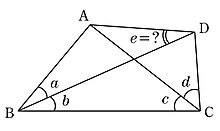
BCEF сияқты төртбұрыш ан деп аталады төртбұрыш оның диагональдары мен қабырғалары арасындағы бұрыштар барлық рационалды бұрыштар болған кезде береді рационал сандар бүкіл шеңбер рационалды сан болатын градуспен немесе басқа бірліктермен өлшенгенде. Лэнглидің басқатырғыштарындағыдан басқа көптеген төртбұрыштар салынған. Олар бірнеше шексіз отбасылар мен қосымша саналы мысалдар жиынтығын құрайды.[5]
Төрт бұрышты жіктеу (бұлар дөңес болмауы керек) барлық көпбұрыштардағы диагональдардың үштік қиылыстарын жіктеуге тең келеді. Бұл шешілді Геррит Бол 1936 жылы (Beantwoording van prijsvraag № 17, Ниеу-Архиф Вискунда 18, 14-66 беттер). Ол шынымен де көпбұрыштардағы диагональдардың барлық бірнеше қиылыстарын (бірнеше қателіктермен болса да) жіктеді. Оның нәтижелері (барлығы қолмен жасалынған) компьютермен расталды және қателер 1998 жылы Бьорн Пунен мен Майкл Рубинштейнмен түзетілді.[6] Мақалада мәселенің тарихы және тұрақты бейнеленген сурет бар триаконтагон және оның диагональдары.
2015 жылы белгісіз жапондық әйел «аэрил ре» лақап атын қолданып, төртбұрыш мәселесінің ерекше сыныбы үшін қарапайым геометрияда дәлелдеу үшін алғашқы белгілі әдісті жариялады (3 айналма әдіс).[7][8][9] Бұл жұмыс Ригбидің 1978 жылғы мақаласында келтірілген үш шешілмеген мәселенің біріншісін шешеді.[5]
Әдебиеттер тізімі
- ^ а б Лэнгли, Э.М. (1922), «Мәселе 644», Математикалық газет, 11: 173.
- ^ а б в Дарлинг, Дэвид (2004), Математиканың әмбебап кітабы: Абракадабрадан Зенон парадокстарына дейін, Джон Вили және ұлдары, б. 180.
- ^ Трипп, Колин (1975), «Қатерлі бұрыштар», Математикалық газет, 59: 98–106, JSTOR 3616644.
- ^ Богомольный, Александр. «80-80-20 үшбұрышы». www.cut-the-knot.org. Алынған 2018-06-03.
- ^ а б Ригби, Дж. Ф. (1978), «Қатерлі төртбұрыштар: геометриялық тәсіл», Математикалық газет, 62 (421): 183–191, дои:10.2307/3616687, МЫРЗА 0513855.
- ^ Пунен, Бьорн; Рубинштейн, Майкл (1998), «Тұрақты көпбұрыштың диагональдары жасаған қиылысу нүктелерінің саны» (PDF), Дискретті математика бойынша SIAM журналы, 11 (1): 135–156.
- ^ Сайто, Хироси (2016), «Адвентитивті төртбұрыштар толығымен қарапайым шешіммен шешілді», Гендайсūгаку (現代 数学) (жапон тілінде), 49 (590): 66–73, ISSN 2187-6495.
- ^ aerile_re (2015-10-27), Ұлы Геометриядан соңғы шақыру (жапон тілінде), мұрағатталған түпнұсқа 2016-04-16.
- ^ Сайто, Хироси (2016-12-11), «3 циркулятор әдісін» енгізу - мақаланың ағылшын тіліндегі аудармасы Гендайзугаку (現代 数学).
Сыртқы сілтемелер
- Бұрыштық Angst, MathPages




































