Эйлер - Бернулли сәулесінің теориясы - Euler–Bernoulli beam theory

Бұл мақала үшін қосымша дәйексөздер қажет тексеру. Өтінемін көмектесіңіз осы мақаланы жақсарту арқылы дәйексөздерді сенімді дерек көздеріне қосу. Ресурссыз материалға шағым жасалуы және алынып тасталуы мүмкін. Дереккөздерді табу: «Эйлер-Бернулли сәулесінің теориясы»  – жаңалықтар  · газеттер  · кітаптар  · ғалым  · JSTOR (Қараша 2008 ж) (Бұл шаблон хабарламасын қалай және қашан жою керектігін біліп алыңыз)

Бұл дірілдейтін шыны сәуле үдеуі, сызықтық тығыздығы, айнымалы қимасының модулі, диссипацияның қандай-да бір түрі, серіппелі ұшымен жүктеме және бос ұшында мүмкін нүктелік масса бар консольды сәуле ретінде модельденуі мүмкін.

Эйлер - Бернулли сәулесінің теориясы (сонымен бірге инженер сәулесінің теориясы немесе классикалық сәулелер теориясы)^[1] жеңілдету болып табылады серпімділіктің сызықтық теориясы жүктемені есептеу құралын ұсынады және ауытқу сипаттамалары сәулелер. Бұл а-ның кішігірім ауытқуларына арналған жағдайды қамтиды сәуле тек бүйірлік жүктемелерге ұшырайды. Бұл ерекше жағдай Тимошенконың сәулелік теориясы. Бұл шамамен 1750 ж.,^[2] дамығанға дейін кең көлемде қолданылмады Эйфель мұнарасы және Айналма дөңгелек 19 ғасырдың аяғында. Осы сәтті демонстрациялардан кейін ол тез арада инженерліктің негізіне айналды және мүмкіндік берді Екінші өнеркәсіптік революция.

Қосымша математикалық модельдер сияқты әзірленді пластина теориясы, бірақ сәуле теориясының қарапайымдылығы оны ғылымдардағы маңызды құралға айналдырады, әсіресе құрылымдық және механикалық инженерия.

Тарих

Нейтралды осьті көрсететін иілген сәуленің көлденең қимасының схемасы.

Алдыңғы консенсус - бұл Галилео Галилей сәулелер теориясын жасауға алғашқы әрекеттерді жасады, бірақ соңғы зерттеулер бұл туралы айтады Леонардо да Винчи бірінші болып шешуші бақылаулар жасады. Да Винчи жетіспеді Гук заңы және есептеу теорияны аяқтау үшін, ал Галилей өзінің дұрыс емес жорамалымен ұсталды.^[3]

Бернулли сәулесі есімімен аталады Джейкоб Бернулли, кім маңызды жаңалық ашты. Леонхард Эйлер және Даниэль Бернулли бірінші болып пайдалы теорияны 1750 ж. жинады.^[4]Сол кезде ғылым және инженерлік Әдетте, бұл өте нақты салалар ретінде қарастырылды және академияның математикалық өніміне қауіпсіздіктің практикалық қосымшаларына сенуге болатындығына күмән көп болды. Көпірлер мен ғимараттар 19 ғасырдың соңына дейін прецедент бойынша жобаланған Эйфель мұнарасы және Айналма дөңгелек теорияның дұрыстығын үлкен ауқымда көрсетті.

Статикалық сәуленің теңдеуі

Эйлер - Бернулли теңдеуі сәуленің арасындағы байланысты сипаттайды ауытқу және қолданылатын жүктеме:^[5]

${ displaystyle { frac { mathrm {d} ^ {2}} { mathrm {d} x ^ {2}}} left (EI { frac { mathrm {d} ^ {2} w} { mathrm {d} x ^ {2}}} оң) = q ,}$

Қисық ${ displaystyle w (x)}$ сәулесінің ауытқуын сипаттайды ${ displaystyle z}$ бағытта ${ displaystyle x}$ (сәуле бір өлшемді объект ретінде модельденгенін еске түсіріңіз). ${ displaystyle q}$ - бұл бөлінген жүктеме, басқаша айтқанда ұзындық бірлігіне келетін күш (аналогы қысым бір ауданға күш болу); функциясы болуы мүмкін ${ displaystyle x}$, ${ displaystyle w}$немесе басқа айнымалылар. ${ displaystyle E}$ болып табылады серпімді модуль және ${ displaystyle I}$ болып табылады ауданның екінші сәті сәуленің көлденең қимасының. ${ displaystyle I}$ көлденең қиманың центроиды арқылы өтетін және қолданылатын жүктеуге перпендикуляр болатын оське қатысты есептелуі керек.^{[N 1]} Айқын, осі бойымен бағытталған сәуле үшін х бірге жүктеу з, сәуленің көлденең қимасы yz жазықтық, ал ауданның тиісті екінші моменті болып табылады

${ displaystyle I = iint z ^ {2} ; dy ; dz,}$

мұнда көлденең қиманың центроиды орын алады деп болжанған ж = з = 0.

Көбінесе, өнім ${ displaystyle EI}$ (ретінде белгілі иілу қаттылығы ) тұрақты болып табылады, сондықтан

${ displaystyle EI { frac { mathrm {d} ^ {4} w} { mathrm {d} x ^ {4}}} = q (x). ,}$

Бірқалыпты, статикалық сәуленің ауытқуын сипаттайтын бұл теңдеу инженерлік практикада кеңінен қолданылады. Ауытқуға арналған кестелік өрнектер ${ displaystyle w}$ жалпы сәулелік конфигурацияларды инженерлік нұсқаулықтан табуға болады. Күрделі жағдайлар үшін ауытқуды Эйлер-Бернулли теңдеуін шешу арқылы анықтауға болады. «тікелей интеграция ", "Маколей әдісі ", "сәттің ауданы әдісі, "конъюгат сәулесінің әдісі ", "виртуалды жұмыс принципі ", "Кастильяноның әдісі ", "икемділік әдісі ", "көлбеу ауытқу әдісі ", "моментті бөлу әдісі «, немесе»тікелей қаттылық әдісі ".

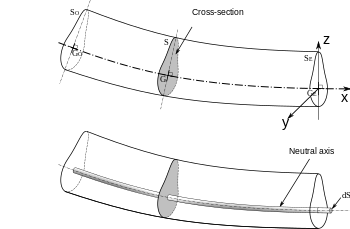
Мұнда белгілердің конвенциялары анықталған, өйткені әдебиеттерде әртүрлі конвенцияларды табуға болады.^[5] Бұл мақалада а оң қол координаттар жүйесі суретте көрсетілгендей қолданылады, Эйлер-Бернулли сәулесінің иілуі. . Бастап ${ displaystyle mathbf {e_ {z}} times mathbf {e_ {x}} = mathbf {e_ {y}}}$ қайда ${ displaystyle mathbf {e_ {x}}}$, ${ displaystyle mathbf {e_ {y}}}$, және ${ displaystyle mathbf {e_ {z}}}$ сәйкесінше х, у және z осьтерінің бағыты бойынша бірлік векторлар болып табылады, y осінің бағыты суретте орналасқан. Позитивті әрекет ететін күштер ${ displaystyle x}$ және ${ displaystyle z}$ бағыттар оң қабылданады. Иілу сәтінің белгісі ${ displaystyle M}$ кесіндінің оң жағындағы иілу моментімен байланысты крутящий вектор оң y бағытта болғанда оң болады (яғни оң мәні ${ displaystyle M}$ төменгі талшықтарда қысу кернеуіне әкеледі). Иілу сәтін осы таңдау арқылы конвенцияға қол жеткізу керек ${ displaystyle dM = Qdx}$, ығысу күші қажет ${ displaystyle Q}$ моменттердің статикалық тепе-теңдігіне қол жеткізу үшін қиманың оң жағында әрекет ету z бағытында оң болады. -Мен күш тепе-теңдігі болуы керек ${ displaystyle dQ = qdx}$, жүктеу қарқындылығы ${ displaystyle q}$ теріс z бағытында оң болуы керек. Скалярлық шамаларға арналған осы белгілік шарттардан басқа, біз кейде векторларды қолданамыз, онда векторлардың бағыттары бірлік векторларды қолдану арқылы айқын болады, ${ displaystyle mathbf {e_ {x}}}$, ${ displaystyle mathbf {e_ {y}}}$, және ${ displaystyle mathbf {e_ {z}}}$.

Ауытқудың дәйекті туындылары ${ displaystyle w}$ маңызды физикалық мағыналары бар: ${ displaystyle dw / dx}$ - сәуленің көлбеуі,

${ displaystyle M = -EI { frac {d ^ {2} w} {dx ^ {2}}}}$

болып табылады иілу сәті сәуледе және

${ displaystyle Q = - { frac {d} {dx}} солға (EI { frac {d ^ {2} w} {dx ^ {2}}} оңға)}$

болып табылады ығысу күші сәуледе.

Эйлер-Бернулли сәулесінің иілуі. Әрбір сәуленің көлденең қимасы бейтарап осіне 90 градусқа тең.

Берілген жүктемеге байланысты ауытқу анықталғаннан кейін сәуледегі кернеулерді жоғарыдағы өрнектерден есептеуге болады.

Иілу теңдеуін шығару

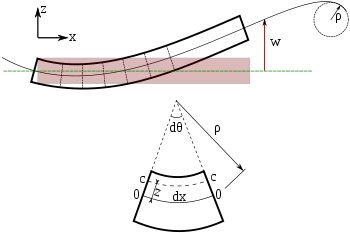
Иілу моменті теңдеуінің машина жасаудағы негізгі мәні болғандықтан, біз қысқа шығаруды қамтамасыз етеміз. Біз полярлық координаттарға ауысамыз. Суреттегі бейтарап осьтің ұзындығы ${ displaystyle rho d theta.}$ Радиалды қашықтықтағы талшықтың ұзындығы ${ displaystyle z}$ бейтарап осінің астында орналасқан ${ displaystyle ( rho + z) d theta.}$ Сондықтан, бұл талшықтың штаммы болып табылады

${ displaystyle { frac { сол жақ ( rho + z- rho оң) d theta} { rho d theta}} = { frac {z} { rho}}.}$

Бұл талшықтың күйзелісі ${ displaystyle E { tfrac {z} { rho}}}$ қайда ${ displaystyle E}$ болып табылады серпімді модуль сәйкес Гук заңы. Дифференциал күш векторы, ${ displaystyle d mathbf {F},}$ осы стресстен туындайтын,

${ displaystyle d mathbf {F} = E { frac {z} { rho}} dA mathbf {e_ {x}}.}$

Бұл суретте көрсетілген қиманың оң жағында қолданылатын дифференциалды күш векторы. Біз оның екенін білеміз ${ displaystyle mathbf {e_ {x}}}$ бағыт, өйткені суретте төменгі жартыдағы талшықтар шиеленісіп тұрғандығы айқын көрінеді. ${ displaystyle dA}$ - талшықтың орналасқан жеріндегі ауданның дифференциалды элементі. Дифференциалды иілу моментінің векторы, ${ displaystyle d mathbf {M}}$ байланысты ${ displaystyle d mathbf {F}}$ арқылы беріледі

${ displaystyle d mathbf {M} = -z mathbf {e_ {z}} times d mathbf {F} = - mathbf {e_ {y}} E { frac {z ^ {2}} { rho}} dA.}$

Бұл өрнек сәуленің төменгі жартысындағы талшықтарға жарамды. Сәуленің жоғарғы жартысындағы талшықтардың өрнегі ұқсас болады, тек момент векторы оң z бағытта болады, ал күш векторы -х бағытта болады, өйткені жоғарғы талшықтар қысылып тұр. Алынған иілу моментінің векторы содан бері -y бағытында болады ${ displaystyle mathbf {e_ {z}} times - mathbf {e_ {x}} = - mathbf {e_ {y}}.}$ Сондықтан, біз сәуленің бүкіл көлденең қимасы бойынша интеграцияланып, аламыз ${ displaystyle mathbf {M}}$ өрнектің оң көлденең қимасына иілу моментінің векторы

${ displaystyle mathbf {M} = int d mathbf {M} = - mathbf {e_ {y}} { frac {E} { rho}} int {z ^ {2}} dA = - mathbf {e_ {y}} { frac {EI} { rho}},}$

қайда ${ displaystyle I}$ болып табылады ауданның екінші сәті. Есептеуден біз қашан екенін білеміз ${ displaystyle { tfrac {dw} {dx}}}$ ол Эйлер-Бернулли сәулесі үшін кішкентай, ${ displaystyle { tfrac {1} { rho}} = { tfrac {d ^ {2} w} {dx ^ {2}}}}$ (${ displaystyle rho}$ болып табылады қисықтық радиусы ). Сондықтан,

${ displaystyle mathbf {M} = - mathbf {e_ {y}} EI {d ^ {2} w over dx ^ {2}}.}$

Бұл векторлық теңдеуді иілу бірлігінің векторлық анықтамасында бөлуге болады (М ey ретінде бағытталған) және иілу теңдеуінде:

${ displaystyle M = -EI {d ^ {2} w over dx ^ {2}}.}$

Динамикалық сәуленің теңдеуі

Соңғы элемент әдісі кең фланецті сәуленің дірілінің моделі (Мен- сәуле ).

Динамикалық сәуленің теңдеуі болып табылады Эйлер – Лагранж теңдеуі келесі әрекет үшін

${ displaystyle S = int _ {t_ {1}} ^ {t_ {2}} int _ {0} ^ {L} left [{ frac {1} {2}} mu left ({ frac { жарым-жартылай w} { жартылай t}} оңға) ^ {2} - { frac {1} {2}} EI солға ({ frac { жарым-жартылай ^ {2} w} { жартылай x ^ {2}}} right) ^ {2} + q (x) w (x, t) right] dxdt.}$

Бірінші мүше кинетикалық энергияны білдіреді ${ displaystyle mu}$ - бұл ұзындық бірлігіндегі масса; екіншісі ішкі күштердің әсерінен болатын потенциалды энергияны (теріс таңбамен қарастырғанда), ал үшінші мүше сыртқы жүктеменің әсерінен потенциалды энергияны білдіреді ${ displaystyle q (x)}$. The Эйлер – Лагранж теңдеуі функционалды минимизациялайтын функцияны анықтау үшін қолданылады ${ displaystyle S}$. Динамикалық Эйлер-Бернулли сәулесі үшін Эйлер-Лагранж теңдеуі болады

${ displaystyle { cfrac { жарым-жартылай ^ {2}} { жартылай x ^ {2}}} сол жаққа (EI { cfrac { жарым-жартылай ^ {2} w} { жартылай x ^ {2}}} оң) = - mu { cfrac { ішіндегі ^ {2} w} { ішінара t ^ {2}}} + q (x)}$

Бөренелерге арналған Эйлер-Лагранж теңдеуін шығару

Бастап Лагранж болып табылады ${ displaystyle { mathcal {L}}: = { tfrac {1} {2}} mu сол жақ ({ frac { жартылай w} { ішінара t}} оңға) ^ {2} - { tfrac {1} {2}} EI солға ({ frac { жартылай ^ {2} w} { жартылай x ^ {2}}} оңға) ^ {2} + q (x) w (x) , t) = { tfrac { mu} {2}} { dot {w}} ^ {2} - { tfrac {EI} {2}} w_ {xx} ^ {2} + qw equiv { mathcal {L}} (x, t, w, { dot {w}}, w_ {xx})}$ сәйкес Эйлер – Лагранж теңдеуі болып табылады ${ displaystyle { cfrac { жарым-жартылай { mathcal {L}}} { жартылай w}} - { frac { жартылай} { жартылай t}} солға ({ frac { жартылай { mathcal {) L}}} { ішінара { нүкте {w}}}} оң) + { frac { жартылай ^ {2}} { жартылай x ^ {2}}} солға ({ frac { жартылай { mathcal {L}}} { ішінара w_ {xx}}} оң) = 0}$ Енді, ${ displaystyle { cfrac { жарым-жартылай { mathcal {L}}} { жартылай w}} = q ~; ~~ { frac { жарым-жартылай { mathcal {L}}} { жартылай { нүкте { w}}}} = mu { dot {w}} ~; ~~ { frac { жарым-жартылай { mathcal {L}}} { жартылай w_ {xx}}} = - EIw_ {xx} ~. }$ Эйлер-Лагранж теңдеуіне қосылуға болады ${ displaystyle q- mu { ddotot {w}} - (EIw_ {xx}) _ {xx} = 0}$ немесе, ${ displaystyle { cfrac { жарым-жартылай ^ {2}} { жартылай x ^ {2}}} сол жаққа (EI { cfrac { жарым-жартылай ^ {2} w} { жартылай x ^ {2}}} оң) = - mu { cfrac { ішіндегі ^ {2} w} { жартылай t ^ {2}}} + q}$ бұл Эйлер-Бернулли сәулесінің динамикасының басқарушы теңдеуі.

Сәуле біртекті болған кезде, ${ displaystyle E}$ және ${ displaystyle I}$ тәуелді емес ${ displaystyle x}$және сәуленің теңдеуі қарапайым:

${ displaystyle EI { cfrac { жарым-жартылай ^ {4} w} { жартылай x ^ {4}}} = - mu { cfrac { жарым-жартылай ^ {2} w} { жартылай t ^ {2} }} + q ,.}$

Еркін діріл

Көлденең жүктеме болмаған кезде, ${ displaystyle q}$, бізде бар еркін діріл теңдеу. Бұл теңдеуді форманың гармоникалық тербелістерінің қосындысына ығысудың Фурье декомпозициясы арқылы шешуге болады.

${ displaystyle w (x, t) = { text {Re}} [{ hat {w}} (x) ~ e ^ {- i omega t}]}$

қайда ${ displaystyle omega}$ - тербеліс жиілігі. Содан кейін, жиіліктің әрбір мәні үшін қарапайым дифференциалдық теңдеуді шеше аламыз

${ displaystyle EI ~ { cfrac { mathrm {d} ^ {4} { hat {w}}} { mathrm {d} x ^ {4}}} - mu omega ^ {2} { қалпақ {w}} = 0 ,.}$

Жоғарыда келтірілген теңдеудің жалпы шешімі мынада

${ displaystyle { hat {w}} = A_ {1} cosh ( beta x) + A_ {2} sinh ( beta x) + A_ {3} cos ( beta x) + A_ {4 } sin ( beta x) quad { text {with}} quad beta: = left ({ frac { mu omega ^ {2}} {EI}} right) ^ {1 / 4}}$

қайда ${ displaystyle A_ {1}, A_ {2}, A_ {3}, A_ {4}}$ тұрақты болып табылады. Бұл тұрақтылар берілген шекаралық шарттардың жиынтығы үшін ерекше. Алайда, орын ауыстырудың шешімі ерекше емес және ол жиілікке байланысты. Бұл шешімдер әдетте келесі түрде жазылады

${ displaystyle { hat {w}} _ {n} = A_ {1} cosh ( beta _ {n} x) + A_ {2} sinh ( beta _ {n} x) + A_ {3 } cos ( beta _ {n} x) + A_ {4} sin ( beta _ {n} x) quad { text {with}}} quad beta _ {n}: = left ( { frac { mu omega _ {n} ^ {2}} {EI}} right) ^ {1/4} ,.}$

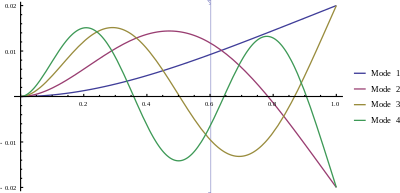
Шамалар ${ displaystyle omega _ {n}}$ деп аталады табиғи жиіліктер сәуленің Ауыстыру шешімдерінің әрқайсысы а деп аталады режимі ал ығысу қисығының пішіні деп аталады режим пішіні.

Мысал: консольды сәуле

Тербелмелі консоль сәулесінің алғашқы төрт режимінің режимі.

Ұзындықтың консольды сәулесінің шекаралық шарттары ${ displaystyle L}$ (бекітілген ${ displaystyle x = 0}$) болып табылады

${ displaystyle { begin {aligned} & { hat {w}} _ {n} = 0 ~, ~~ { frac {d { hat {w}} _ {n}} {dx}} = 0 quad { text {at}} ~~ x = 0 & { frac {d ^ {2} { hat {w}} _ {n}} {dx ^ {2}}} = 0 ~, ~~ { frac {d ^ {3} { hat {w}} _ {n}} {dx ^ {3}}} = 0 quad { text {at}} ~~ x = L ,. end {aligned}}}$

Егер біз осы шарттарды қолданатын болсақ, тривиальды емес шешімдер тек қана болған жағдайда ғана болады${ displaystyle cosh ( beta _ {n} L) , cos ( beta _ {n} L) + 1 = 0 ,.}$Бұл сызықтық емес теңдеуді сандық түрде шешуге болады. Алғашқы тамырлар β₁ L / π = 0.59686..., β₂ L / π = 1.49418..., β₃ L / π = 2.50025..., β₄ L / π = 3.49999..., ...

Дірілдің сәйкес табиғи жиіліктері болып табылады

${ displaystyle omega _ {1} = beta _ {1} ^ {2} { sqrt { frac {EI} { mu}}} = { frac {3.5161} {L ^ {2}}} { sqrt { frac {EI} { mu}}} ~, ~~ нүктелер}$

Шектік шарттарды ығысуға арналған шешімнен режим формаларын анықтау үшін де қолдануға болады:

${ displaystyle { hat {w}} _ {n} = A_ {1} { Bigl [} ( cosh beta _ {n} x- cos beta _ {n} x) + { frac { cos beta _ {n} L + cosh beta _ {n} L} { sin beta _ {n} L + sinh beta _ {n} L}} ( sin beta _ {n} x - sinh beta _ {n} x) { Bigr]}}$

Белгісіз тұрақты (әрқайсысы үшін тұрақты болатындай тұрақты) ${ displaystyle n}$), ${ displaystyle A_ {1}}$, жалпы алғанда күрделі, бастапқы шарттармен анықталады ${ displaystyle t = 0}$ сәуленің жылдамдығы мен орын ауыстыруы туралы. Әдетте мәні ${ displaystyle A_ {1} = 1}$ режим фигураларын салу кезінде қолданылады. Өткізілмеген мәжбүрлі мәселенің шешімдері қозғалыс жиілігі мен табиғи жиілікке сәйкес келгенде шексіз орын ауыстыруларға ие ${ displaystyle omega _ {n}}$, яғни сәуле алады резонанс. Сәуленің табиғи жиіліктері сол жиіліктерге сәйкес келеді резонанс орын алуы мүмкін.

Мысалы: қолдау көрсетілмеген (еркін) сәуле

Эйлер-Бернулли сәулесінің дірілдеуінің алғашқы төрт режимі.

Еркін сәуле - бұл тіректерсіз сәуле.^[6] Ұзындықтың еркін сәулесінің шекаралық шарттары L бастап созылып жатыр х= 0-ден х= L келесі түрде беріледі:

${ displaystyle { frac {d ^ {2} { hat {w}} _ {n}} {dx ^ {2}}} = 0 ~, ~~ { frac {d ^ {3} { hat {w}} _ {n}} {dx ^ {3}}} = 0 quad { text {at}} ~~ x = 0 , { text {and}} , L ,.}$

Егер біз осы шарттарды қолданатын болсақ, тривиальды емес шешімдер тек қана болған жағдайда ғана болады${ displaystyle cosh ( beta _ {n} L) , cos ( beta _ {n} L) -1 = 0 ,.}$

Бұл сызықтық емес теңдеуді сандық түрде шешуге болады. Алғашқы тамырлар β₁ L / π = 1.50562..., β₂ L / π = 2.49975..., β₃ L / π = 3.50001..., β₄ L / π = 4.50000...

Дірілдің сәйкес табиғи жиіліктері:

${ displaystyle omega _ {1} = beta _ {1} ^ {2} { sqrt { frac {EI} { mu}}} = { frac {22.3733} {L ^ {2}}} { sqrt { frac {EI} { mu}}} ~, ~~ нүктелер}$

Шектік шарттарды ығысуға арналған шешімнен режим формаларын анықтау үшін де қолдануға болады:

${ displaystyle { hat {w}} _ {n} = A_ {1} { Bigl [} ( cos beta _ {n} x + cosh beta _ {n} x) - { frac { cos beta _ {n} L- cosh beta _ {n} L} { sin beta _ {n} L- sinh beta _ {n} L}} ( sin beta _ {n} x + sinh beta _ {n} x) { Bigr]}}$

Консольді сәуле сияқты, белгісіз тұрақтылар at бастапқы шарттарымен анықталады ${ displaystyle t = 0}$ сәуленің жылдамдығы мен орын ауыстыруы туралы. Сондай-ақ, шешілмеген мәжбүрлі мәселені шешу кезінде қозғалыс жиілігі мен табиғи жиілікке сәйкес келген кезде шектеусіз орын ауыстырулар болады ${ displaystyle omega _ {n}}$.

Стресс

Ауытқудан басқа сәуленің теңдеуі сипаттайды күштер және сәттер және осылайша сипаттау үшін қолдануға болады стресс. Осы себепті Эйлер-Бернулли сәулесінің теңдеуі кең қолданылады инженерлік иілу кезіндегі арқалықтардың беріктігін (сонымен қатар ауытқуын) анықтау үшін, әсіресе азаматтық және механикалық.

Екі иілу сәті және ығысу күші сәуледе стресс тудыруы мүмкін. Ығысу күшінің әсерінен болатын кернеу бейтарап ось сәуленің (сәуленің ені, t, сәуленің көлденең қимасы бойынша тұрақты болғанда; әйтпесе бірінші момент пен сәуленің енін қамтитын интегралды нақты көлденең қимада бағалау керек) және максималды созылу кернеуі не жоғарғы, не төменгі беттерде орналасқан. Осылайша максимум негізгі стресс сәуледе жер бетінде де, орталықта да емес, жалпы аймақта болуы мүмкін. Алайда, ығысу күшінің кернеулері ең қарапайым сәулелерден басқаларының иілу моментінің кернеулерімен салыстырғанда шамалы, сонымен қатар стресс концентрациясы әдетте беттерде пайда болады, яғни сәуледе максималды кернеу беткі қабатта болуы мүмкін.

Қарапайым немесе симметриялы иілу

Бүктелген сәуленің элементі: талшықтар концентрлі доғаларды құрайды, жоғарғы талшықтар сығылған және төменгі талшықтар созылған.

Бейтарап жазықтыққа перпендикуляр жазықтыққа симметриялы болатын көлденең қималар үшін сәуленің әсерінен болатын созылу кернеуі келесі түрде көрсетілуі мүмкін:

${ displaystyle sigma = { frac {Mz} {I}} = - zE ~ { frac { mathrm {d} ^ {2} w} { mathrm {d} x ^ {2}}}. ,}$

Мұнда, ${ displaystyle z}$ - бейтарап осьтен қызығушылық нүктесіне дейінгі қашықтық; және ${ displaystyle M}$ иілу сәті. Бұл теңдеу соны меңзейтінін ескеріңіз таза иілу (оң белгісі) бейтарап осінде нөлдік, сәуленің «жоғарғы жағында» оң (созылу) кернеуін, ал сәуленің төменгі жағында теріс (қысу) кернеу тудырады; сонымен қатар максималды кернеу жоғарғы қабатта, ал төменгі деңгей төменгі деңгейде болатындығын білдіреді. Бұл иілу кернеуі осьтік берілген кернеулермен қабаттасуы мүмкін, бұл бейтарап (нөлдік кернеулер) осінің жылжуын тудырады.

Көлденең қимадағы максималды кернеулер

Сәуленің кесінді модулін анықтауда қолданылатын шамалар.

Көлденең қимадағы созылудың максималды кернеуі орналасқан жерінде болады ${ displaystyle z = c_ {1}}$ және максималды қысу кернеуі орналасқан жерде болады ${ displaystyle z = -c_ {2}}$ онда көлденең қиманың биіктігі ${ displaystyle h = c_ {1} + c_ {2}}$. Бұл стресстер

${ displaystyle sigma _ {1} = { cfrac {Mc_ {1}} {I}} = { cfrac {M} {S_ {1}}} ~; ~~ sigma _ {2} = - { cfrac {Mc_ {2}} {I}} = - { cfrac {M} {S_ {2}}}}$

Шамалар ${ displaystyle S_ {1}, S_ {2}}$ болып табылады бөлім модульдері^[5] және ретінде анықталады

${ displaystyle S_ {1} = { cfrac {I} {c_ {1}}} ~; ~~ S_ {2} = { cfrac {I} {c_ {2}}}}$

Қима модулі сәуленің қимасы туралы барлық маңызды геометриялық ақпаратты бір шамада біріктіреді. Сәуле екі есе симметриялы болған жағдайда, ${ displaystyle c_ {1} = c_ {2}}$ және бізде бір бөлім модулі бар ${ displaystyle S = I / c}$.

Эйлер-Бернулли сәулесіндегі штамм

Бізге өрнек керек штамм бейтарап беттің ауытқуы бойынша Эйлер-Бернулли сәулесіндегі кернеулерді ауытқумен байланыстыру керек. Бұл өрнекті алу үшін біз деформация кезінде бейтарап бетке нормальдар қалыпты болып қалады және ауытқулар аз болады деген болжамды қолданамыз. Бұл болжамдар сәуленің радиус шеңберінің доғасына иілуін білдіреді ${ displaystyle rho}$ (1-суретті қараңыз) және деформация кезінде бейтарап бетінің ұзындығы өзгермейтіндігін.^[5]

Келіңіздер ${ displaystyle mathrm {d} x}$ деформацияланған күйдегі бейтарап бет элементінің ұзындығы. Шағын ауытқулар үшін элемент иілгеннен кейін ұзындығын өзгертпейді, бірақ радиус шеңберінің доғасына айналады ${ displaystyle rho}$. Егер ${ displaystyle mathrm {d} theta}$ - бұл осы доға арқылы түсірілген бұрыш, содан кейін ${ displaystyle mathrm {d} x = rho ~ mathrm {d} theta}$.

Енді элементтің тағы бір сегментін қашықтықта қарастырайық ${ displaystyle z}$ бейтарап бетінен жоғары. Бұл элементтің бастапқы ұзындығы ${ displaystyle mathrm {d} x}$. Алайда, иілгеннен кейін элементтің ұзындығы айналады ${ displaystyle mathrm {d} x '= ( rho -z) ~ mathrm {d} theta = mathrm {d} x-z ~ mathrm {d} theta}$. Сәуленің сол сегментіндегі штамм арқылы беріледі

${ displaystyle varepsilon _ {x} = { cfrac { mathrm {d} x '- mathrm {d} x} { mathrm {d} x}} = - { cfrac {z} { rho} } = - kappa ~ z}$

қайда ${ displaystyle kappa}$ болып табылады қисықтық сәуленің Бұл бізге бейтарап бетінен қашықтыққа байланысты сәуленің осьтік кернеуін береді. Дегенмен, бізге қисықтық радиусы мен сәуленің ауытқуы арасындағы байланысты табу керек ${ displaystyle w}$.

Қисықтық пен сәуленің ауытқуы арасындағы байланыс

Р сәуленің бейтарап бетіндегі қашықтықтағы нүкте болсын ${ displaystyle x}$ шығу тегінен ${ displaystyle (x, z)}$ координаттар жүйесі. Сәуленің көлбеуі бейтарап бетпен жасалған бұрышқа шамамен тең ${ displaystyle x}$- сәуле теориясында кездесетін кішігірім бұрыштарға арналған. Сондықтан, осы жуықтаумен,

${ displaystyle theta (x) = { cfrac { mathrm {d} w} { mathrm {d} x}}}$

Сондықтан, шексіз элемент үшін ${ displaystyle mathrm {d} x}$, қатынас ${ displaystyle mathrm {d} x = rho ~ mathrm {d} theta}$ деп жазуға болады

${ displaystyle { cfrac {1} { rho}} = { cfrac { mathrm {d} theta} { mathrm {d} x}} = { cfrac { mathrm {d} ^ {2} w} { mathrm {d} x ^ {2}}} = kappa}$

Демек, сәуленің штаммы келесі түрде көрсетілуі мүмкін

${ displaystyle varepsilon _ {x} = - z kappa}$

Стресс-деформация қатынастары

Біртекті үшін изотропты сызықтық серпімді материал, стресс штамммен байланысты ${ displaystyle sigma = E varepsilon}$, қайда ${ displaystyle E}$ болып табылады Янг модулі. Демек, Эйлер-Бернулли сәулесіндегі кернеулер келесідей болады

${ displaystyle sigma _ {x} = - zE { cfrac { mathrm {d} ^ {2} w} { mathrm {d} x ^ {2}}}}$

Жоғарыда көрсетілген қатынас осьтік кернеу мен иілу моменті арасындағы қатынаспен салыстырғанда, әкелетінін ескеріңіз

${ displaystyle M = -EI { cfrac { mathrm {d} ^ {2} w} { mathrm {d} x ^ {2}}}}$

Ығысу күші берілгендіктен ${ displaystyle Q = mathrm {d} M / mathrm {d} x}$, бізде де бар

${ displaystyle Q = -EI { cfrac { mathrm {d} ^ {3} w} { mathrm {d} x ^ {3}}}}$

Шектік ойлар

Сәулелік теңдеуде төртінші ретті туынды бар ${ displaystyle x}$. Бірегей шешім табу ${ displaystyle w (x, t)}$ бізге төрт шекаралық шарт қажет. Шектік шарттар әдетте модельдейді тіректер, сонымен қатар олар нүктелік жүктемелерді, үлестірілген жүктемелер мен моменттерді модельдей алады. The қолдау немесе орын ауыстырудың шекаралық шарттары орын ауыстыру мәндерін бекіту үшін қолданылады (${ displaystyle w}$) және айналулар (${ displaystyle mathrm {d} w / mathrm {d} x}$) шекарада. Мұндай шекаралық шарттар деп те аталады Дирихлеттің шекаралық шарттары. Жүктеме мен моменттің шекаралық шарттары жоғары туындыларды қамтиды ${ displaystyle w}$ және ұсыну импульс ағыны. Ағынның шекаралық шарттары деп те аталады Неймандық шекаралық шарттар.

Мысал ретінде а консоль көршілес суретте көрсетілгендей бір ұшында кіріктірілген, ал екінші жағында бос сәуле. Кіріктірілген сәуленің соңында сәуленің жылжуы немесе айналуы болмайды. Бұл сол жақта иілу де, көлбеу де нөлге тең болатындығын білдіреді. Сәуленің бос ұшында сыртқы иілу моменті қолданылмайтындықтан, сол жерде иілу моменті нөлге тең. Сонымен қатар, егер сәулеге сыртқы күш әсер етпесе, бос ұшындағы ығысу күші де нөлге тең болады.

Қабылдау ${ displaystyle x}$ сол жақ ұшының координаты ${ displaystyle 0}$ және оң жақ соңы ${ displaystyle L}$ (сәуленің ұзындығы), бұл тұжырымдар келесі шекаралық шарттардың жиынтығына айналады (делік ${ displaystyle EI}$ тұрақты):

${ displaystyle w | _ {x = 0} = 0 quad; quad { frac { жарым-жартылай w} { жартылай x}} { bigg |} _ {x = 0} = 0 qquad { mbox {(белгіленген соңы)}} ,}$

Консольды сәуле.

${ displaystyle { frac { жарым-жартылай ^ {2} w} { жартылай x ^ {2}}} { bigg |} _ {x = L} = 0 quad; quad { frac { qism ^ {3} w} { жартылай x ^ {3}}} { bigg |} _ {x = L} = 0 qquad { mbox {(бос аяғы)}} ,}$

Қарапайым тіреуіш (түйреуіш немесе ролик) пучкадағы нүктелік күшке тең, ол сәуленің сол жерде орналасуын бекітетін етіп реттеледі. Бекітілген тіреуіш немесе қапсырма, нүктенің күші мен нүктенің айналу моментінің тіркесіміне тең, ол дәл сол сәтте сәуленің орналасуын және көлбеуін бекітетін етіп реттеледі. Нүктелік күштер мен моменттер, тіректерден болсын немесе тікелей қолданылған болса да, сәулені сегменттердің жиынтығына бөледі, олардың арасында сәуленің теңдеуі сегіздіктің әр соңында екі шекаралық шартты ескере отырып, үздіксіз шешім береді. Өнім деп есептесек EI тұрақты және анықтаушы болып табылады ${ displaystyle lambda = F / EI}$ қайда F - нүктелік күштің шамасы және ${ displaystyle tau = M / EI}$ қайда М - нүктелік моменттің шамасы, кейбір жалпы жағдайларға сәйкес шекаралық шарттар төмендегі кестеде келтірілген. Нақты туындысының өзгеруі w шекара арқылы х ұлғаюы арқылы белгіленеді ${ displaystyle Delta}$ содан кейін сол туынды Мысалға, ${ displaystyle Delta w '' = w '' (x +) - w '' (x-)}$ қайда ${ displaystyle w '(x +)}$ мәні болып табылады ${ displaystyle w ''}$ жоғарғы сегменттің төменгі шекарасында, ал ${ displaystyle w '(x-)}$ мәні болып табылады ${ displaystyle w ''}$ төменгі сегменттің жоғарғы шекарасында. Егер белгілі бір туынды мәндері шекара бойынша үзіліссіз ғана емес, сонымен қатар тұрақты болса, шекаралық шарт жазылады, мысалы, ${ displaystyle Delta w '' = 0 ^ {*}}$ ол екі бөлек теңдеуді құрайды (мысалы, ${ displaystyle w '(x -) = w' '(x +)}$ = бекітілген).

Шекара	${ displaystyle w '' '}$	${ displaystyle w ''}$	${ displaystyle w '}$	${ displaystyle w}$
Қысқыш			${ displaystyle Delta w '= 0 ^ {*}}$	${ displaystyle Delta w = 0 ^ {*}}$
Қарапайым қолдау		${ displaystyle Delta w '' = 0}$	${ displaystyle Delta w '= 0}$	${ displaystyle Delta w = 0 ^ {*}}$
Нүктелік күш	${ displaystyle Delta w '' '= lambda}$	${ displaystyle Delta w '' = 0}$	${ displaystyle Delta w '= 0}$	${ displaystyle Delta w = 0}$
Нүктелік момент	${ displaystyle Delta w '' '= 0}$	${ displaystyle Delta w '' = tau}$	${ displaystyle Delta w '= 0}$	${ displaystyle Delta w = 0}$
Тегін аяғы	${ displaystyle w '' '= 0}$	${ displaystyle w '' = 0}$
Соңында қысқыш			${ displaystyle w '}$ тұрақты	${ displaystyle w}$ тұрақты
Қарапайым қолдау		${ displaystyle w '' = 0}$		${ displaystyle w}$ тұрақты
Соңындағы нүктелік күш	${ displaystyle w '' '= pm lambda}$	${ displaystyle w '' = 0}$
Соңындағы моментті көрсетіңіз	${ displaystyle w '' '= 0}$	${ displaystyle w '= = pm tau}$

Нүктелік күштер мен моменттер екі сегменттің арасында орналасқан бірінші жағдайларда төрт шекаралық шарт бар, екеуі төменгі сегмент үшін, ал екеуі жоғарғы үшін. Күштер мен моменттер сәуленің бір ұшына түскенде, сол шетте қолданылатын екі шекаралық шарт бар. Соңындағы нүктелік күштер мен моменттердің белгісі төменгі ұшына оң, жоғарғы ұшына теріс болады.

Ойлар жүктелуде

Қолданылатын жүктемелер шекаралық шарттар арқылы немесе функция арқылы ұсынылуы мүмкін ${ displaystyle q (x, t)}$ бұл сыртқы үлестірілген жүктемені білдіреді. Таратылған жүктемені пайдалану көбінесе қарапайымдылыққа қолайлы. Шекаралық жағдайлар, алайда, көбінесе контекстке байланысты жүктемелерді модельдеу үшін қолданылады; бұл тәжірибе әсіресе дірілді талдау кезінде жиі кездеседі.

Табиғат бойынша бөлінген жүктеме көбінесе бөлік түрінде ұсынылады, өйткені іс жүзінде жүктеме әдетте үздіксіз функция болып табылмайды. Нүктелік жүктемелерді көмегімен модельдеуге болады Dirac delta функциясы. Мысалы, ұзындықтағы статикалық біркелкі консольды сәулені қарастырайық ${ displaystyle L}$ жоғары нүктелік жүктеме арқылы ${ displaystyle F}$ ақыр соңында қолданылады. Шектік шарттарды қолдана отырып, оны екі жолмен модельдеуге болады. Бірінші тәсілде берілген нүктелік жүктеме бос ұшында қолданылатын ығысу күшімен жуықталады. Бұл жағдайда басқару теңдеуі мен шекаралық шарттар:

${ displaystyle { begin {aligned} & EI { frac { mathrm {d} ^ {4} w} { mathrm {d} x ^ {4}}} = 0 & w | _ {x = 0} = 0 quad; quad { frac { mathrm {d} w} { mathrm {d} x}} { bigg |} _ {x = 0} = 0 quad; quad { frac { mathrm {d} ^ {2} w} { mathrm {d} x ^ {2}}} { bigg |} _ {x = L} = 0 quad; quad -EI { frac { mathrm { d} ^ {3} w} { mathrm {d} x ^ {3}}} { bigg |} _ {x = L} = F , end {aligned}}}$

Сонымен қатар, біз Dirac функциясы арқылы нүктелік жүктемені үлестірім ретінде ұсына аламыз. Бұл жағдайда теңдеу және шекаралық шарттар болады

${ displaystyle { begin {aligned} & EI { frac { mathrm {d} ^ {4} w} { mathrm {d} x ^ {4}}} = F delta (xL) & w | _ {x = 0} = 0 quad; quad { frac { mathrm {d} w} { mathrm {d} x}} { bigg |} _ {x = 0} = 0 quad; quad { frac { mathrm {d} ^ {2} w} { mathrm {d} x ^ {2}}} { bigg |} _ {x = L} = 0 , end {aligned}}}$

Ығысу күшінің шекаралық шарты (үшінші туынды) жойылғанын ескеріңіз, әйтпесе қайшылықтар туындауы мүмкін. Бұлар баламалы шекаралық есептер және екеуі де шешім береді

${ displaystyle w = { frac {F} {6EI}} (3Lx ^ {2} -x ^ {3}) , ~.}$

Әр түрлі жерлерде бірнеше нүктелік жүктемелерді қолдану әкеледі ${ displaystyle w (x)}$ біртіндеп функция. Dirac функциясын қолдану мұндай жағдайларды айтарлықтай жеңілдетеді; әйтпесе сәулені бөліктерге бөлуге тура келеді, олардың әрқайсысы төрт шекаралық шартты бөлек шешеді. Жақсы ұйымдастырылған функциялар отбасы Сингулярлық функциялары Dirac функциясы үшін стенография ретінде жиі қолданылады, оның туынды және оның антидеривативтер.

Динамикалық құбылыстар жүктемені бөлудің сәйкес формаларын таңдау арқылы статикалық сәулелік теңдеуді қолдану арқылы модельдеуге болады. Мысал ретінде, ақысыз діріл жүктеме функциясын қолдану арқылы сәуленің есебін жүргізуге болады:

${ displaystyle q (x, t) = mu { frac { ішіндегі ^ {2} w} { жартылай t ^ {2}}} ,}$

қайда ${ displaystyle mu}$ болып табылады массаның тығыздығы міндетті түрде тұрақты емес. Осы уақытқа тәуелді жүктеме кезінде сәулелік теңдеу а болады дербес дифференциалдық теңдеу:

${ displaystyle { frac { жарымын ^ {2}} { жартылай x ^ {2}}} сол (EI { frac { жартылай ^ {2} w} { жартылай x ^ {2}}} оң) = - mu { frac { ішіндегі ^ {2} w} { жартылай t ^ {2}}}.}$

Тағы бір қызықты мысал константамен айналатын сәуленің ауытқуын сипаттайды бұрыштық жиілік туралы ${ displaystyle omega}$:

${ displaystyle q (x) = mu omega ^ {2} w (x) ,}$

Бұл центрге тарту күші тарату. Бұл жағдайда, ${ displaystyle q}$ орын ауыстыру функциясы (тәуелді айнымалы), ал сәулелік теңдеу автономды болады қарапайым дифференциалдық теңдеу.

Мысалдар

Үш нүктелі иілу

The үш нүктелік иілу сынағы механикадағы классикалық эксперимент. Бұл екі білік тіректеріне тірелген және сәуленің ортасында шоғырланған жүктеме түсіретін сәуленің жағдайын білдіреді. Қайшы абсолютті мәнде тұрақты: бұл орталық жүктеменің жартысы, P / 2. Ол сәуленің ортасында белгісін өзгертеді. Иілу моменті бір шетінен сызықты түрде өзгереді, мұнда ол 0, ал оның абсолюттік мәні PL / 4 болатын центр - үзілу қаупі ең маңызды жерде, сәуленің деформациясы үшінші дәрежелі полиноммен сипатталады. иілу сәттері (жартысы симметриялы).${ displaystyle M}$), ығысу күштері (${ displaystyle Q}$) және ауытқулар (${ displaystyle w}$) орталық нүктелік жүктеме әсер ететін сәуле үшін және асимметриялық нүктелік жүктеме төмендегі кестеде келтірілген.^[5]

Тарату	Макс. мәні
Орталық жүктемесі бар қарапайым арқалық
${ displaystyle M (x) = { begin {case} { frac {Px} {2}}, & { mbox {for}} 0 leq x leq { tfrac {L} {2}} { frac {P (Lx)} {2}}, & { mbox {for}} { tfrac {L} {2}}$	${ displaystyle M_ {L / 2} = { tfrac {PL} {4}}}$
${ displaystyle Q (x) = { begin {case} { frac {P} {2}}, & { mbox {for}} 0 leq x leq { tfrac {L} {2}} { frac {-P} {2}}, & { mbox {for}} { tfrac {L} {2}}$	${ displaystyle | Q_ {0} | = | Q_ {L} | = { tfrac {P} {2}}}$
${ displaystyle w (x) = { begin {case} - { frac {Px (4x ^ {2} -3L ^ {2})} {48EI}}, & { mbox {for}} 0 leq x leq { tfrac {L} {2}} { frac {P (xL) (L ^ {2} -8Lx + 4x ^ {2})} {48EI}}, & { mbox {for }} { tfrac {L} {2}}$	${ displaystyle w_ {L / 2} = { tfrac {PL ^ {3}} {48EI}}}$
Асимметриялық жүктемесі бар қарапайым арқалық
${ displaystyle M (x) = { begin {case} { tfrac {Pbx} {L}}, & { mbox {for}} 0 leq x leq a { tfrac {Pbx} {L }} - P (xa) = { tfrac {Pa (Lx)} {L}}, & { mbox {for}} a$	${ displaystyle M_ {B} = { tfrac {Pab} {L}}}$
${ displaystyle Q (x) = { begin {case} { tfrac {Pb} {L}}, & { mbox {for}} 0 leq x leq a { tfrac {Pb} {L }} - P, & { mbox {for}} a$	${ displaystyle Q_ {A} = { tfrac {Pb} {L}}}$ ${ displaystyle Q_ {C} = { tfrac {Pa} {L}}}$
${ displaystyle w (x) = { begin {case} { tfrac {Pbx (L ^ {2} -b ^ {2} -x ^ {2})} {6LEI}}, & 0 leq x leq a { tfrac {Pbx (L ^ {2} -b ^ {2} -x ^ {2})} {6LEI}} + { tfrac {P (xa) ^ {3}} {6EI}} , & a$	${ displaystyle w _ { mathrm {max}} = { tfrac {{ sqrt {3}} Pb (L ^ {2} -b ^ {2}) ^ { frac {3} {2}}} { 27LEI}}}$ кезінде ${ displaystyle x = { sqrt { tfrac {L ^ {2} -b ^ {2}} {3}}}}$

Консоль арқалықтары

Мәселелердің тағы бір маңызды класы жатады консоль сәулелер. Иілу сәттері (${ displaystyle M}$), ығысу күштері (${ displaystyle Q}$) және ауытқулар (${ displaystyle w}$) консольдік сәуле үшін бос ұшында нүктелік жүктеме және біркелкі үлестірілген жүктеме төмендегі кестеде келтірілген.^[5]

Тарату	Макс. мәні
Соңғы жүктемесі бар консольды арқалық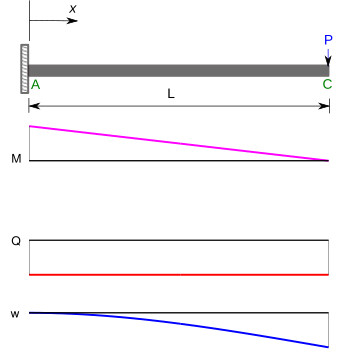
${ displaystyle M (x) = P (L-x)}$	${ displaystyle M_ {A} = PL}$
${ displaystyle Q (x) = P}$	${ displaystyle Q _ { mathrm {max}} = P}$
${ displaystyle w (x) = { tfrac {Px ^ {2} (3L-x)} {6EI}}}$	${ displaystyle w_ {C} = { tfrac {PL ^ {3}} {3EI}}}$
Біркелкі үлестірілген жүктеме бар консольды арқалық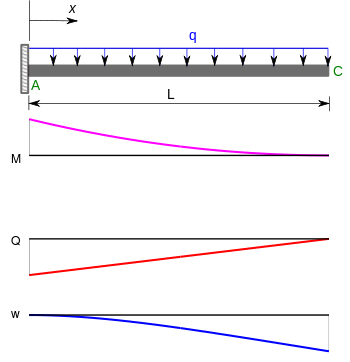
${ displaystyle M (x) = - { tfrac {q (L ^ {2} -2Lx + x ^ {2})} {2}}}$	${ displaystyle M_ {A} = { tfrac {qL ^ {2}} {2}}}$
${ displaystyle Q (x) = q (L-x),}$	${ displaystyle Q_ {A} = qL}$
${ displaystyle w (x) = { tfrac {qx ^ {2} (6L ^ {2} -4Lx + x ^ {2})} {24EI}}}$	${ displaystyle w_ {C} = { tfrac {qL ^ {4}} {8EI}}}$

Бірнеше жиі кездесетін конфигурацияларға арналған шешімдер материалдардың механикасы оқулықтарында және инженерлік оқулықтарда қол жетімді.

Статикалық анықталмаған сәулелер

The иілу сәттері және ығысу күштері Эйлер-Бернулли сәулелерін көбінесе статикалық тепе-теңдікті қолдану арқылы анықтауға болады күштер және сәттер. Алайда, белгілі бір шекаралық шарттар үшін реакциялар саны тәуелсіз тепе-теңдік теңдеулерінен асып кетуі мүмкін.^[5] Мұндай сәулелер деп аталады статикалық тұрғыдан анықталмаған.

Төмендегі суретте көрсетілген кіріктірілген сәулелер статикалық түрде анықталмаған. To determine the stresses and deflections of such beams, the most direct method is to solve the Euler–Bernoulli beam equation with appropriate boundary conditions. But direct analytical solutions of the beam equation are possible only for the simplest cases. Therefore, additional techniques such as linear superposition are often used to solve statically indeterminate beam problems.

The superposition method involves adding the solutions of a number of statically determinate problems which are chosen such that the boundary conditions for the sum of the individual problems add up to those of the original problem.

(a) Uniformly distributed load q.	(b) Linearly distributed load with maximum q0
${displaystyle M_{mathrm {max} }={cfrac {qL^{2}}{12}}~;~~w_{mathrm {max} }={cfrac {qL^{4}}{384EI}}}$	${displaystyle M_{mathrm {max} }={cfrac {qL^{2}}{300}}[3{sqrt {30}}-10]~;~~w_{mathrm {max} }={cfrac {qL^{4}}{2500EI}}[75-7{sqrt {105}}]}$
(c) Concentrated load P	(d) Moment M0

Another commonly encountered statically indeterminate beam problem is the cantilevered beam with the free end supported on a roller.^[5] The bending moments, shear forces, and deflections of such a beam are listed below:

Тарату	Макс. мәні
${displaystyle M(x)=-{ frac {q}{8}}(L^{2}-5Lx+4x^{2})}$	${displaystyle {egin{aligned}M_{B}&=-{ frac {9qL^{2}}{128}}{mbox{ at }}x={ frac {5L}{8}}M_{A}&={ frac {qL^{2}}{8}}end{aligned}}}$
${displaystyle Q(x)=-{ frac {q}{8}}(8x-5L)}$	${displaystyle Q_{A}=-{ frac {5qL}{8}}}$
${displaystyle w(x)={ frac {qx^{2}}{48EI}}(3L^{2}-5Lx+2x^{2})}$	${displaystyle w_{mathrm {max} }={ frac {(39-55{sqrt {33}})}{65,536}}{ frac {qL^{4}}{EI}}{mbox{ at }}x={ frac {15-{sqrt {33}}}{16}}L}$

Кеңейтімдер

The kinematic assumptions upon which the Euler–Bernoulli beam theory is founded allow it to be extended to more advanced analysis. Simple superposition allows for three-dimensional transverse loading. Using alternative құрылтай теңдеулері can allow for жабысқақ немесе пластик beam deformation. Euler–Bernoulli beam theory can also be extended to the analysis of curved beams, beam buckling, composite beams, and geometrically nonlinear beam deflection.

Euler–Bernoulli beam theory does not account for the effects of transverse қайшы штамм. As a result, it underpredicts deflections and overpredicts natural frequencies. For thin beams (beam length to thickness ratios of the order 20 or more) these effects are of minor importance. For thick beams, however, these effects can be significant. More advanced beam theories such as the Тимошенконың сәулелік теориясы (developed by the Russian-born scientist Стивен Тимошенко ) have been developed to account for these effects.

Large deflections

Euler–Bernoulli beam

The original Euler–Bernoulli theory is valid only for infinitesimal strains and small rotations. The theory can be extended in a straightforward manner to problems involving moderately large rotations provided that the strain remains small by using the фон Карман штамдар.^[7]

The Euler–Bernoulli hypotheses that plane sections remain plane and normal to the axis of the beam lead to displacements of the form

${displaystyle u_{1}=u_{0}(x)-z{cfrac {mathrm {d} w_{0}}{mathrm {d} x}}~;~~u_{2}=0~;~~u_{3}=w_{0}(x)}$

Using the definition of the Lagrangian Green strain from finite strain theory, we can find the von Karman strains for the beam that are valid for large rotations but small strains. These strains have the form

${displaystyle {egin{aligned}varepsilon _{11}&={cfrac {mathrm {d} u_{0}}{dx}}-z{cfrac {mathrm {d} ^{2}w_{0}}{mathrm {d} x^{2}}}+{frac {1}{2}}left[left({cfrac {mathrm {d} u_{0}}{mathrm {d} x}}-z{cfrac {mathrm {d} ^{2}w_{0}}{mathrm {d} x^{2}}} ight)^{2}+left({cfrac {mathrm {d} w_{0}}{mathrm {d} x}} ight)^{2} ight]varepsilon _{22}&=0varepsilon _{33}&={frac {1}{2}}left({cfrac {mathrm {d} w_{0}}{mathrm {d} x}} ight)^{2}varepsilon _{23}&=0varepsilon _{31}&={frac {1}{2}}left({cfrac {mathrm {d} w_{0}}{mathrm {d} x}}-{cfrac {mathrm {d} w_{0}}{mathrm {d} x}} ight)-{frac {1}{2}}left[left({cfrac {mathrm {d} u_{0}}{mathrm {d} x}}-z{cfrac {mathrm {d} ^{2}w_{0}}{mathrm {d} x^{2}}} ight)left({cfrac {mathrm {d} w_{0}}{mathrm {d} x}} ight) ight]varepsilon _{12}&=0end{aligned}}}$

Бастап виртуалды жұмыс принципі, the balance of forces and moments in the beams gives us the equilibrium equations

${displaystyle {egin{aligned}{cfrac {mathrm {d} N_{xx}}{mathrm {d} x}}+f(x)&=0{cfrac {mathrm {d} ^{2}M_{xx}}{mathrm {d} x^{2}}}+q(x)+{cfrac {mathrm {d} }{mathrm {d} x}}left(N_{xx}{cfrac {mathrm {d} w_{0}}{mathrm {d} x}} ight)&=0end{aligned}}}$

қайда ${ displaystyle f (x)}$ is the axial load, ${ displaystyle q (x)}$ is the transverse load, and

${displaystyle N_{xx}=int _{A}sigma _{xx}~mathrm {d} A~;~~M_{xx}=int _{A}zsigma _{xx}~mathrm {d} A}$

To close the system of equations we need the құрылтай теңдеулері that relate stresses to strains (and hence stresses to displacements). For large rotations and small strains these relations are

${displaystyle {egin{aligned}N_{xx}&=A_{xx}left[{cfrac {mathrm {d} u_{0}}{dx}}+{frac {1}{2}}left({cfrac {mathrm {d} w_{0}}{mathrm {d} x}} ight)^{2} ight]-B_{xx}{cfrac {mathrm {d} ^{2}w_{0}}{mathrm {d} x^{2}}}M_{xx}&=B_{xx}left[{cfrac {du_{0}}{mathrm {d} x}}+{frac {1}{2}}left({cfrac {mathrm {d} w_{0}}{mathrm {d} x}} ight)^{2} ight]-D_{xx}{cfrac {mathrm {d} ^{2}w_{0}}{mathrm {d} x^{2}}}end{aligned}}}$

қайда

${displaystyle A_{xx}=int _{A}E~mathrm {d} A~;~~B_{xx}=int _{A}zE~mathrm {d} A~;~~D_{xx}=int _{A}z^{2}E~mathrm {d} A~.}$

Саны ${ displaystyle A_ {xx}}$ болып табылады extensional stiffness,${displaystyle B_{xx}}$ is the coupled extensional-bending stiffness, және ${displaystyle D_{xx}}$ болып табылады иілу қаттылығы.

For the situation where the beam has a uniform cross-section and no axial load, the governing equation for a large-rotation Euler–Bernoulli beam is

${displaystyle EI~{cfrac {mathrm {d} ^{4}w}{mathrm {d} x^{4}}}-{frac {3}{2}}~EA~left({cfrac {mathrm {d} w}{mathrm {d} x}} ight)^{2}left({cfrac {mathrm {d} ^{2}w}{mathrm {d} x^{2}}} ight)=q(x)}$

Сондай-ақ қараңыз

• Қолданбалы механика
• Иілу
• Иілу сәті
• Буклет
• Иілгіш қаттылық
• Generalised beam theory
• Пластиналар теориясы
• Сэндвич теориясы
• Ығысу және момент диаграммасы
• Сингулярлық функциясы
• Штамм (материалтану)
• Тимошенконың сәулелік теориясы
• Үш сәт теоремасы (Clapeyron's theorem)
• Үш нүктелік иілу сынағы

Ескертулер

Әдебиеттер тізімі

• E. A. Witmer (1991–1992). "Elementary Bernoulli-Euler Beam Theory". MIT Unified Engineering Course Notes. pp. 5–114 to 5–164.

Сыртқы сілтемелер

• Beam stress & deflection, beam deflection tables