Жою орнатылды - Delone set
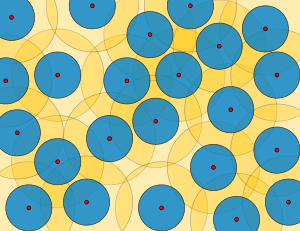
Математикалық теориясында метрикалық кеңістіктер, ε-торлар, ε-орамдар, ε жабындар, біркелкі дискретті жиынтықтар, салыстырмалы тығыз жиынтықтар, және Жою жиындары (атымен Борис Делоне ) нүктелер жиынтығының бірнеше өзара байланысты анықтамалары және орау радиусы және жабу радиусы бұл жиынтықтар олардың қаншалықты жақсы орналасқандығын өлшейді. Бұл жиынтықтардың қосымшалары бар кодтау теориясы, жуықтау алгоритмдері, және теориясы квазикристалдар.
Анықтамалар
Егер (М,г.) - бұл метрикалық кеңістік, және X ішкі бөлігі болып табылады М, содан кейін орау радиусы туралы X тең жартысы шексіз мүшелерінің арасындағы қашықтық X. Егер орау радиусы р, содан кейін радиустың шарлары ашық р нүктелерінде орналасқан X барлығы бір-бірінен бөлінеді, және әрбір ашық доп нүктелердің біреуіне бағытталған X радиусы 2р қалғандарынан бөлінеді X. The жабу радиусы туралы X сандардың шексіздігі р әрбір нүктесі М қашықтықта орналасқан р кем дегенде бір ұпай X; яғни, ең кіші радиус, сол нүктенің центрінде орналасқан осы радиустың жабық шарлары X барлығында бар М олардың бірлестігі ретінде. Ан ε- орау жиынтық X ing орау радиусыε/ 2 (баламалы, минималды арақашықтық ≥ ε), ан ε жабыны жиынтық X жабу радиусы ≤ε, және net-тор жиынтығы болып табылады ε-бума және ан ε- жабу. Жиынтық біркелкі дискретті егер оның нөлдік емес орау радиусы болса және салыстырмалы түрде тығыз егер оның соңғы жабу радиусы болса. A Жою орнатылды бұл біркелкі дискретті және салыстырмалы түрде тығыз жиынтық; осылайша, әрқайсысы ε-net Delone, бірақ керісінше емес.[1][2]
Торлардың құрылысы
Жоғарыдағы анықтамалардың ішіндегі ең шектеу ретінде As-торларды құру, ең болмағанда, ε-орамалар, ε-жабындар және Delone жиынтықтары сияқты қиын. Алайда, кез келген уақытта М бар жақсы тапсырыс беру, трансфиниттік индукция ε-тор құруға болатындығын көрсетеді N, қосу арқылы N тапсырыс кезіндегі алдыңғы нүктелер жиынтығына дейінгі арақашықтықтардың шегі кем дегенде every болатын әр нүкте. Шектелген өлшемді эвклид кеңістігіндегі ақырғы нүктелер жиынтығы үшін әр нүктені тұрақты уақытта оны диаметрі cells ұяшықтар торына түсіру арқылы және хэш-кесте жақын орналасқан ұяшықтардың қайсысының нүктелері бар екенін тексеру үшін N; осылайша, бұл жағдайда ε-торын құруға болады сызықтық уақыт.[3][4]
Неғұрлым жалпы ақырғы немесе ықшам метрикалық кеңістіктер, баламалы алгоритмі Тео Гонсалес негізінде ең алыс жүру ақырлы ε-тор құру үшін пайдалануға болады. Бұл алгоритм желіні баптандырады N бос болуы керек, содан кейін бірнеше рет қосады N ең алыс нүкте М бастап N, байланыстарды ерікті түрде бұзу және барлық нүктелер болған кезде тоқтатуМ distance қашықтықта орналасқанN.[5] Жылы екі еселенетін өлшемді кеңістіктер, Гонсалестің алгоритмін O (n журналn) нүктелердің жиынтығы үшін олардың ең алыс және жақын арақашықтықтары арасындағы полиномдық қатынасы бар және ерікті нүктелер жиынтығына бірдей уақыт аралығында жуықталған уақыт.[6]
Қолданбалар
Кодтау теориясы
Теориясында қателерді түзететін кодтар, a болатын метрикалық кеңістік блок коды C айталық, бекітілген ұзындықтағы жіптерден тұрады n, өлшемді алфавитті қабылдады q (деп ойлауға болады векторлар ), бірге Химинг метрикасы. Бұл кеңістікті деп белгілейді . Бұл метрикалық кеңістіктің жабу радиусы мен орау радиусы кодтың қателерді түзету мүмкіндігімен байланысты.
Жақындау алгоритмдері
Хар-Пелед және Райхель (2013) жобалау үшін «тор және қара өрік» деп атайтын алгоритмдік парадигманы сипаттаңыз жуықтау алгоритмдері нүктелер жиынтығында анықталған геометриялық оңтайландыру есептерінің жекелеген түрлері үшін Евклид кеңістігі. Осы типтегі алгоритм келесі әрекеттерді орындау арқылы жұмыс істейді:
- Кездейсоқ нүктені таңдаңыз б нүктеден бастап, жақын көршісін табыңыз q, және ε арасындағы қашықтыққа орнатыңыз б және q.
- Ε шешімнің оңтайлы мәнінен (шамамен) үлкен немесе кіші екенін тексеріңіз (шешіліп жатқан оңтайландырудың белгілі бір проблемасына тән техниканы қолданып)
- Егер ол үлкенірек болса, кірістен жақын көршісі ε-ден алыс нүктелерді алып тастаңыз
- Егер ол кішірек болса, ε-тор құрыңыз N, кірмейтін нүктелерді алып тастаңыз N.
Екі жағдайда да, қалған ұпайлардың болжамды саны тұрақты коэффициентке азаяды, сондықтан уақыт тестілеу қадамымен басым болады. Олар көрсеткендей, бұл парадигманы жылдам жуықтау алгоритмдерін құру үшін пайдалануға болады k-орталығы кластерлеу, медианалық қашықтықтағы жұп нүктелерді табу және соған байланысты бірнеше есептер.
А деп аталатын торлардың иерархиялық жүйесі ағаш, қолданылуы мүмкін екі еселенетін өлшемді кеңістіктер салу жақсы бөлінген жұптық ыдырау, геометриялық кілттер, және шамамен жақын көршілер.[6][7]
Кристаллография
Үшін ұпайлар үшін Евклид кеңістігі, жиынтық X Бұл Мейер жиналды егер ол салыстырмалы түрде тығыз болса және оның айырмашылық жиынтығы X − X біркелкі дискретті. Эквивалентті, X егер бұл екеуі де болса Meyer жиынтығы X және X − X Delone. Мейер жиынтықтары аталған Ив Мейер, кім оларды енгізді (негізінде әр түрлі, бірақ эквивалентті анықтама бар гармоникалық талдау ) үшін математикалық модель ретінде квазикристалдар. Оларға нүктелер жиынтығы кіреді торлар, Пенроздың плиткалары, және Минковский сомалары осы жиындардан ақырғы жиындар.[8]
The Вороной жасушалары симметриялы Delone жиындарының формасы кеңістікті толтыратын полиэдра деп аталады плезиоэдра.[9]
Сондай-ақ қараңыз
Пайдаланылған әдебиеттер
- ^ Кларксон, Кеннет Л. (2006), «Үшбұрыштарды қолдану арқылы құру ε-желілер «, STOC'06: Есептеулер теориясы бойынша жыл сайынғы 38-ші ACM симпозиумының материалдары, Нью-Йорк: ACM, 326–335 б., дои:10.1145/1132516.1132564, ISBN 1595931341, МЫРЗА 2277158.
- ^ Кейбір дереккөздер пайдаланады «ε-нет «мұнда» деп аталатыны үшін «ε-қаптау »; қараңыз, мысалы. Сазерленд, В. (1975), Метрикалық және топологиялық кеңістіктермен таныстыру, Oxford University Press, б. 110, ISBN 0-19-853161-3, Zbl 0304.54002.
- ^ Хар-Пелед, С. (2004), «Кластерлік қозғалыс», Дискретті және есептеу геометриясы, 31 (4): 545–565, дои:10.1007 / s00454-004-2822-7, МЫРЗА 2053498.
- ^ Хар-Пелед, С .; Raichel, B. (2013), «Net and prune: Евклидтік қашықтыққа арналған есептердің алгоритмі», STOC'13: Есептеу теориясы бойынша 45-ші ACM симпозиумының материалдары, 605-614 б., arXiv:1409.7425.
- ^ Гонсалес, Т. Ф. (1985), «Максимумаралық аралықты барынша азайту үшін кластерлеу», Теориялық информатика, 38 (2–3): 293–306, дои:10.1016/0304-3975(85)90224-5, МЫРЗА 0807927.
- ^ а б Хар-Пелед, С .; Мендель, М. (2006), «Төмен өлшемді метрикалардағы торлардың жылдам құрылысы және олардың қолданылуы», Есептеу бойынша SIAM журналы, 35 (5): 1148–1184, arXiv:cs / 0409057, дои:10.1137 / S0097539704446281, МЫРЗА 2217141.
- ^ Кравтхамер, Роберт; Ли, Джеймс Р. (2004), «Навигациялық торлар: жақындықты іздеудің қарапайым алгоритмдері», Дискретті алгоритмдер бойынша 15-ші ACM-SIAM симпозиумының материалдары (SODA '04), Филадельфия, Пенсильвания, АҚШ: Өнеркәсіптік және қолданбалы математика қоғамы, 798–807 б., ISBN 0-89871-558-X.
- ^ Муди, Роберт В. (1997), «Мейер жиынтықтары және олардың дуалдары», Ұзақ диапазондағы апериодтық тәртіптің математикасы (Ватерлоо, ОН, 1995), НАТО-ның жетілдірілген ғылыми институттары, C сериясы: математикалық және физикалық ғылымдар, 489, Дордрехт: Kluwer Academic Publishers, 403–441 б., МЫРЗА 1460032.
- ^ Грюнбаум, Бранко; Шефард, Г. (1980), «Үйлесімді плиткалармен қаптау», Американдық математикалық қоғамның хабаршысы, Жаңа сериялар, 3 (3): 951–973, дои:10.1090 / S0273-0979-1980-14827-2, МЫРЗА 0585178.
Сыртқы сілтемелер
- Жою орнатылды - Tilings энциклопедиясы

