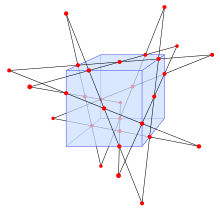
Quadrisecant - Quadrisecant

Жылы геометрия, а квадрисекант немесе квадрисекантты сызық а қисық Бұл түзу қисықтың төрт нүктесі арқылы өтеді.Әр түйінді қисық үш өлшемді Евклид кеңістігі квадрисеканты бар. Квадрисеканттарының саны алгебралық қисық жылы күрделі проекциялық кеңістік арқылы алынған формула бойынша есептеуге болады Артур Кэйли. Quadrisecants қисық сызықтар сонымен бірге байланысты басқарылатын беттер және Шләфли алтыға қосылды конфигурация.
Түйін теориясында
Үшөлшемді Евклид кеңістігі, әрқайсысы тривиальды емес қолға үйрету түйін немесе сілтеме квадрисеканты бар. Бастапқыда түйін болған жағдайда құрылған көпбұрыштар және тегіс түйіндер Эрика Паннвиц,[1]бұл нәтиже түйіндерге дейін кеңейтілген жалпы позиция және нөлдермен байланыстырады сілтеме нөмірі,[2]және кейінірек барлық нейтривиальды қарапайым түйіндер мен сілтемелерге.[3]
Паннвиц тораппен шектелген жергілікті тегіс ашық дискідегі ерекше квадрисексанттардың саны минималды шекара даралықтарының функциясымен төмен болатындығын дәлелдеді.[1][4] Morton & Mond (1982) берілген түйіннің квадрисексанттарының саны әрқашан кем дегенде болады деп болжайды n(n - 1) / 2, қайда n болып табылады қиылысу нөмірі түйін.[2][4] Алайда осы болжамға қарсы мысалдар табылды.[4]
Екі компонентті сілтемелерде квадрисеканттегі нүктелер екі компоненттің кезектесіп пайда болатын квадрисеканты бар,[2] және жеке емес түйіндердің төрт нүктесі бар төрт квадрисеканты бар, циклдік түрде тапсырыс берді сияқты а,б,c,г. торапта ретімен пайда болады а,c,б,г. квадрисекант бойымен.[5] Осы ауыспалы квадрисексанттардың болуы туралы айту үшін қолдануға болады Фари-Милнор теоремасы, а төменгі шекара үстінде жалпы қисықтық ерекше емес түйін.[5] Quadrisecants сонымен қатар төменгі шекараларды табу үшін қолданылған арқан ұзындығы түйіндер.[6]
Алгебралық геометрияда
Артур Кэйли ан квадрисеканты санының формуласын шығарды алгебралық қисық үш өлшемді күрделі проекциялық кеңістік, оның функциясы ретінде дәрежесі және түр.[7] Дәреженің қисығы үшін г. және тұқым ж, квадрисеканттардың саны[8]
Қисық сызықтар
Үшөлшемді Евклид кеңістігі, төрт жиынтығы қисық сызықтар жылы жалпы позиция немесе екі квадрисеканты бар (сонымен бірге осы тұрғыда аталады) көлденең ) немесе жоқ. Төрт жолдың кез-келген үшеуі а-ны анықтайды екі еселенген үстіңгі қабат, онда басқарылатын жолдардың екі жиынтығының бірінде берілген үш жол бар, ал екінші ереже берілген жолдарға арналған трисеканттардан тұрады. Егер берілген сызықтардың төртіншісі осы бетті тесіп өтсе, оның екі қиылысу нүктесі екі квадрисекантада орналасады; егер ол жер бетінен бөлінген болса, онда квадрисеканттар болмайды.[9]
Сызық жиынтығының квадрисексанттары құрылыста маңызды рөл атқарады Шләфли алтыға қосылды, а конфигурация 30 қиылыста өзара қиылысатын он екі сызық. Егер бес жол болса амен (үшін мен = 1,2,3,4,5) үш өлшемді кеңістікте берілген, осылайша бесеуі де жалпы сызықпен қиылысады б6 бірақ жалпы жағдайда, содан кейін сызықтардың төрт төрттіктерінің әрқайсысы орналасады амен екінші квадрисеканты бар бменжәне бес жол бмен осылайша түзілгендердің барлығы ортақ сызықпен қиылысады а6. Бұл он екі сызық пен қиылыстың 30 нүктесі аменбj қос алтылықты құрайды.[10][11]
Әдебиеттер тізімі
- ^ а б Паннвиц, Эрика (1933), «Eine elementargeometrische Eigenschaft von Verschlingungen und Knoten», Mathematische Annalen, 108 (1): 629–672, дои:10.1007 / BF01452857.
- ^ а б c Мортон, Хью Р.; Mond, David M. Q. (1982), «Квадрисеканты жоқ тұйық қисықтар», Топология, 21: 235–243, дои:10.1016/0040-9383(82)90007-6, МЫРЗА 0649756.
- ^ Куперберг, Грег (1994), «тораптар мен сілтемелердің квадрисеканты», Түйін теориясы журналы және оның рамификасы, 3: 41–50, arXiv:математика / 9712205, дои:10.1142 / S021821659400006X, МЫРЗА 1265452.
- ^ а б c Джин, Джо Таек (2005), «Шағын қиылысқан тораптардың квадрисеканты», Түйін теориясындағы физикалық және сандық модельдер (PDF), Сер. Бәрі, 36, Әлемдік ғылыми. Publ., Сингапур, 507–523 бет, дои:10.1142/9789812703460_0025, МЫРЗА 2197955.
- ^ а б Денне, Элизабет Джейн (2004), Түйіндердің ауыспалы квадрисеканты, Ph.D. тезис, Урбан-Шампейндегі Иллинойс университеті, arXiv:математика / 0510561, Бибкод:2005 ж. ..... 10561D.
- ^ Денне, Элизабет; Дяо, Юанан; Салливан, Джон М. (2006), «Quadrisecants тораптың ұзындығына жаңа төменгі шектер береді», Геометрия және топология, 10: 1–26, arXiv:математика / 0408026, дои:10.2140 / gt.2006.10.1, МЫРЗА 2207788.
- ^ Кейли, Артур (1863), Лондон Корольдік қоғамының философиялық операциялары, 153, 453-483 бет, JSTOR 108806.
- ^ Гриффитс, Филлип; Харрис, Джозеф (2011), Алгебралық геометрияның принциптері, Wiley Classics кітапханасы, 52, Джон Вили және ұлдары, б. 296, ISBN 9781118030776.
- ^ Хилберт, Дэвид; Кон-Воссен, Стефан (1952), Геометрия және қиял (2-ші басылым), Нью-Йорк: Челси, б. 164, ISBN 978-0-8284-1087-8.
- ^ Шлафли, Людвиг (1858), Кейли, Артур (ред.), «Үшінші реттің бетіндегі жиырма жеті сызықты анықтауға және жер бетіндегі сызықтардың шындығына сүйене отырып, осындай беттерді түрлерден алуға тырысу», Тоқсан сайынғы таза және қолданбалы математика журналы, 2: 55–65, 110–120.
- ^ Коксетер, H. S. M. (2006), «Өзара жанасатын төрт шеңбердің абсолютті қасиеті», Евклидтік емес геометриялар, Математика. Қолдану. (N. Y.), 581, Нью-Йорк: Спрингер, 109–114 б., дои:10.1007/0-387-29555-0_5, МЫРЗА 2191243. Коксетер Шлафлидің құрылысын қайталайды және оның дұрыстығының жеңілдетілген дәлелдеріне бірнеше сілтемелер келтіреді.