Қиылысу - Intersection

Бұл мақала кең математикалық ұғым туралы. Жолдар түйісетін жерді қараңыз Жол қиылысы. Басқа мақсаттар үшін қараңыз Қиылыс (айыру).
The шеңбер (қара) қиылысады түзу (күлгін) екі нүктеде (қызыл). Диск (сары) ішіндегі сызықты қиып өтеді сызық сегменті екі қызыл нүкте арасында.
Екі дискінің қиылысы (қызыл) (ақ және қызыл қара шекаралары бар).
D және E қиылысы сұрғылт күлгін түсте көрсетілген. A, B, C, D немесе E кез келгенімен қиылысы - бұл бос жиын.

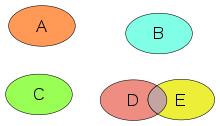
Жылы математика, қиылысу екі немесе одан да көп объектілер басқа, әдетте «кішірек» объект болып табылады. Барлық объектілер белгілі бір жалпыға жатады деп болжануда ғарыш ішінен басқа жиынтық теориясы, мұнда ерікті жиындардың қиылысы анықталады. Қиылысу - бұл негізгі ұғымдардың бірі геометрия. Интуитивті түрде екі немесе одан да көп қиылысу нысандар - бұл әрбір бастапқы объектілерде жатқан жаңа объект. Қиылысу әртүрлі болуы мүмкін геометриялық фигуралар, бірақ а нүкте а-да ең көп кездеседі жазықтық геометриясы.

Анықтамалар әр түрлі жағдайда әр түрлі болады: жиынтық теориясы кішігірім объект үлкен объектіде жатыр деген ойды рәсімдейді қосу, және жиындардың қиылысы қалыптасады элементтер барлық қиылысатын жиындарға жатады. Бұл әрдайым анықталған, бірақ болуы мүмкін бос. Түсу геометриясы қиылысын анықтайды (әдетте, пәтерлер ) төменгі объект ретінде өлшем Бұл оқиға әрбір түпнұсқа объектілерге. Бұл тәсілде қиылысу кейде анықталмаған болуы мүмкін, мысалы параллель түзулер. Екі жағдайда да қиылысу ұғымы сенім артады логикалық байланыс.

Алгебралық геометрия қиылыстарды өзіндік тәсілмен анықтайды қиылысу теориясы.Евклидтік геометрия жазық және қатты пішіндердің қиылысуларымен айналысады.

Бірегейлік

Қиылысты құрайтын нүктелер (жоғарыдағы суретте) сияқты бірнеше қарабайыр объект болуы мүмкін. Қиылысты ортақ объектілердің барлығына бірдей қарауға болады (яғни қиылысу) жұмыс нәтижелері а орнатылды немесе мүмкін) бірнеше қиылысатын нысандар (мүмкін нөл ).

Жиынтық теорияда

Жолдың барлық орналасу жиынтығына сәйкес келетіндігін ескере отырып, екі жолдың (жасыл, көк) қиылысына (көгілдір) олардың жиынтықтарының қиылысына сәйкес келеді.
Негізгі мақала: Қиылысу (жиындар теориясы)

Екі жиынтықтың қиылысы A және B екеуінде де болатын элементтер жиынтығы A және B. Рәміздерде,

.[1]

Мысалы, егер A = {1, 3, 5, 7} және B = {1, 2, 4, 6} содан кейін A ∩ B = {1}. Неғұрлым егжей-тегжейлі мысал (шексіз жиынтықтарды қамтитын):

A = {х жұп бүтін }
B = {х 3} -ге бөлінетін бүтін сан

Тағы бір мысал ретінде, 5 саны емес жиынының қиылысында қамтылған жай сандар {2, 3, 5, 7, 11,…} және жиынтығы жұп сандар {2, 4, 6, 8, 10,…}, өйткені 5 болғанымен болып табылады жай сан, ол емес тіпті. Шын мәнінде, 2 саны - бұл екі жиынның қиылысуындағы жалғыз сан. Бұл жағдайда қиылысудың математикалық мәні бар: 2 саны жалғыз жай сан болып табылады.

Евклидтік геометрияда

Қосымша ақпарат: Қиылысу (Евклидтік геометрия)

Ескерту

Қиылысу арқылы белгіленеді U + 2229 ∩ ҚИЫЛЫС бастап Юникодты математикалық операторлар.

Таңба U + 2229 ∩ бірінші қолданған Герман Грассманн жылы Die Ausdehnungslehre von 1844 ж қиылысуға мамандандырылмаған жалпы жұмыс белгісі ретінде. Сол жерден оны қолданған Джузеппе Пеано (1858-1932) қиылысы үшін, 1888 ж Calcolo geometrico secondo l'Ausdehnungslehre di H. Grassmann.[2][3]

Джузеппе Пеано 1908 жылы өз кітабында екіден астам кластардың жалпы қиылысы мен бірігуі үшін үлкен белгілерді жасады. Формулярлық математика.[4][5]

Сондай-ақ қараңыз

Әдебиеттер тізімі

  1. ^ Верещагин, Николай Константинович; Шен, Александр (2002-01-01). Негізгі жиынтық теориясы. Американдық математикалық со. ISBN  9780821827314.
  2. ^ Пеано, Джузеппе (1888-01-01). Calcolo geometrico secondo l'Ausdehnungslehre di H. Grassmann: preceduto dalle operazioni della logica deduttiva (итальян тілінде). «Торино»: Фрателли Бокка.
  3. ^ Каджори, Флориан (2007-01-01). Математикалық жазбалардың тарихы. Торино: Cosimo, Inc. ISBN  9781602067141.
  4. ^ Пеано, Джузеппе (1908-01-01). Formulario математикасы, томо V (итальян тілінде). Торино: Edizione cremonese (Факсимиле-Репринттегі Римде, 1960). б. 82. OCLC  23485397.
  5. ^ Жиынтық теориясы мен логикасының шартты белгілерінің алғашқы қолданылуы

Сыртқы сілтемелер