Жасырын аттрактор - Hidden attractor
Осы мақаланың тақырыбы Уикипедияға сәйкес келмеуі мүмкін жалпы ескерту нұсқаулығы. (Тамыз 2020) (Бұл шаблон хабарламасын қалай және қашан жою керектігін біліп алыңыз) |
Ішінде бифуркация теориясы, шектелген тербеліс стационарлық жиынтықтың тұрақтылығын жоғалтпай туатын а деп аталады жасырын тербеліс. Жылы сызықтық емес бақылау теория, шектелген күйлері бар уақыт инвариантты басқару жүйесінде жасырын тербелістің тууы, стационар күйлердің жергілікті тұрақтылығы жаһандық тұрақтылықты білдіретін параметрлер шеңберінде, шекарадан өтуді білдіреді (мысалы, қараңыз). Калманның болжамдары ). Егер жасырын тербеліс (немесе ықшам ішкі жиынын толтыратын осындай жасырын тербелістер жиынтығы болса фазалық кеңістік туралы динамикалық жүйе ) барлық жақын тербелістерді тартады, сонда ол а деп аталады жасырын аттрактор. Үшін динамикалық жүйе жаһандық тартымдылыққа ие бірегей тепе-теңдік нүктесімен жасырын тартқыштың тууы моностаттылықтан екі тұрақтылыққа дейінгі мінез-құлықтың сапалы өзгеруіне сәйкес келеді. Жалпы жағдайда динамикалық жүйе болып шығуы мүмкін көпсатылы және жергілікті өмір сүреді тартқыштар фазалық кеңістікте. Тривиальды тартқыштар кезінде, яғни. тұрақты тепе-теңдік нүктелері, іздеуді аналитикалық немесе сандық жолмен оңай табуға болады мерзімді және ретсіз тартқыштар күрделі проблемаға айналуы мүмкін (мысалы, қараңыз) Гильберттің 16-шы есебінің екінші бөлімі ).
Жергілікті аттракторды физикалық немесе сандық экспериментте анықтау үшін бастапқы жүйенің күйін таңдау керек аттракцион бассейні және өтпелі процесстен кейін жүйенің күйі осы бастапқы күйден бастап, тартқышты қалай елестететінін байқаңыз. The аттракторларды жасырын немесе өздігінен қозғалатын деп жіктеу тартымдылық бассейндерін ашу және жергілікті жерлерді іздеу қиындықтарын бейнелейді тартқыштар ішінде фазалық кеңістік.
Анықтама.[1][2][3] Егер тартылыс бассейні тепе-теңдік нүктелерінің белгілі бір маңайымен қиылыспаса, аттракторды жасырын тартқыш деп атайды; әйтпесе ол өзін-өзі қоздыратын аттрактор деп аталады.
Аттракторлардың жасырын немесе өзін-өзі толғандыратын жіктемесі енгізілген Г.Леонов және Н.Кузнецов жасырынның ашылуына байланысты Chua аттракторы [4][5][6][7]2009 жылы алғаш рет. Сол сияқты, фазалық кеңістіктегі тарту бассейні ретінде міндетті түрде ашық көршілікке ие болмайтын, ерікті шектелген тербеліс өздігінен қозғалатын немесе жасырын тербеліс ретінде жіктеледі.

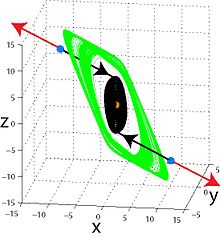

Өзін-өзі қызықтыратын тартқыштар
Өзін-өзі қоздыратын тартқыш үшін оның тартылу бассейні тұрақсыз тепе-теңдікпен байланысты, демек, өзін-өзі қоздыратын аттракторларды стандартты есептеу процедурасы арқылы сандық түрде табуға болады, онда өтпелі процестен кейін траектория көршілес аймақтан басталады. тұрақсыз тепе-теңдік, тербеліс күйіне ауысады, содан кейін оны іздейді (мысалы, қараңыз) өздігінен тербеліс процесс). Осылайша, өзін-өзі қызықтыратын аттракциондар, тіпті жағдайда бірге өмір сүреді көп тұрақтылық, сандық түрде оңай ашылып, бейнеленуі мүмкін. Ішінде Лоренц жүйесі, классикалық параметрлер үшін аттрактор барлық қолданыстағы тепе-теңдікке қатысты өзін-өзі қызықтырады және олардың маңайынан кез-келген траекториямен көрінуі мүмкін; бірақ кейбір басқа параметрлер мәндері үшін хаотикалық тартқышпен қатар өмір сүретін екі тривиальды тартқыш бар, ол тек нөлдік тепе-теңдікке қатысты өзін-өзі қоздырады. Классикалық аттракциондар Ван дер Пол, Белуосов – Жаботинский, Рёслер, Чуа, Хенон динамикалық жүйелер өздігінен қозғалады.
Болжам - бұл өзін-өзі толғандыратын Ляпунов өлшемі тұрақсыз тепе-теңдіктің бірінің Ляпунов өлшемінен аспайды, оның тұрақсыз коллекторы тарту бассейнімен қиылысып, аттракторды көзге елестетеді.[8]
Жасырын аттракциондар
Жасырын аттракторлардың тартымдылық бассейндері бар, олар тепе-теңдікпен байланыссыз және фазалық кеңістіктің бір жерінде «жасырылған». Мысалы, жасырын тартқыштар тепе-теңдіксіз жүйелердегі тартқыштар: мысалы. айналмалы электромеханикалық динамикалық жүйелер Зоммерфельд әсері (1902), тек бір тепе-теңдігі бар жүйелерде тұрақты, мысалы: қарсы мысалдар Айзерманның болжамдары (1949) және Калманның болжамдары (1957) сызықтық емес басқару жүйелерінің моностаттылығы туралы. Бірінші теориялық мәселелердің бірі - екінші бөлігі Гильберттің 16-шы есебінің екінші бөлімі кірістірілген тұрақты шекті циклдар периодты тартқыштар жасырылған екі өлшемді көпмүшелік жүйелердегі шекті циклдердің саны мен өзара орналасуы туралы. Жасырын аттрактор ұғымы көптеген қолданбалы динамикалық модельдерде жасырын тартқыштарды ашудың катализаторына айналды.[1][9][10]
Жалпы, жасырын тартқыштардың проблемасы жүйенің динамикасы үшін мұндай күйлерді бақылау немесе болжау үшін жалпы тікелей әдістердің болмауында (мысалы, қараңыз) [11]). Екі өлшемді жүйелер үшін жасырын тербелістерді аналитикалық әдістер арқылы зерттеуге болады (мысалы, нәтижелерді қараңыз) Гильберттің 16-шы есебінің екінші бөлімі ), тұрақсыздықты және тербелістерді зерттеу үшін сызықтық емес көпөлшемді жүйелерде сандық әдістер жиі қолданылады.Көп өлшемді жағдайда траекторияларды кездейсоқ бастапқы мәліметтермен интеграциялау жасырын тартқыштың оқшаулануын қамтамасыз етуі мүмкін емес, өйткені тарту бассейні мүмкін өте аз болуы керек, ал тартқыш өлшемінің өзі қарастырылатын жүйенің өлшемінен әлдеқайда аз болуы мүмкін, сондықтан көп өлшемді кеңістікте жасырын тартқыштардың сандық локализациясы үшін арнайы аналитикалық-сандық есептеу процедураларын жасау қажет,[1][12][8] бұл жасырын тербелістің тарту аймағында бастапқы деректерді таңдауға мүмкіндік береді (онда тепе-теңдік аудандары жоқ), содан кейін траекториялы есептеуді жүзеге асыруға мүмкіндік береді. гомотопия және сандық жалғасы: ұқсас жүйелер тізбегі құрылады, мысалы, бірінші (бастапқы) жүйе үшін тербелмелі ерітіндіні сандық есептеу үшін бастапқы деректерді аналитикалық жолмен алуға болады, содан кейін осы басталатын тербелісті бір жүйеден екінші жүйеге ауыстыру басқасы сандық түрде жүреді.
Әдебиеттер тізімі
- ^ а б в Леонов Г.А .; Кузнецов Н.В. (2013). «Динамикалық жүйелердегі жасырын тартқыштар. Гильберт-Колмогоров, Айзерман және Кальмандағы жасырын тербелістерден бастап, Чуа тізбегіндегі жасырын хаотикалық аттракторға дейін». Халықаралық қолданбалы ғылымдар мен инженериядағы бифуркация және хаос журналы. 23 (1): 1330002–219. Бибкод:2013 IJBC ... 2330002L. дои:10.1142 / S0218127413300024.
- ^ Брагин В.О .; Вагайцев В.И .; Кузнецов Н.В .; Леонов Г.А. (2011). «Сызықты емес жүйелердегі жасырын тербелістерді табу алгоритмдері. Айзерман және Кальман болжамдары және Чуа тізбектері» (PDF). Халықаралық компьютерлік және жүйелік ғылымдар журналы. 50 (5): 511–543. дои:10.1134 / S106423071104006X. S2CID 21657305.
- ^ Леонов, Г.А .; Кузнецов, Н.В .; Мокаев, Т.Н. (2015). «Конвективті сұйықтық қозғалысын сипаттайтын Лоренцке ұқсас жүйеде гомоклиникалық орбиталар және өздігінен қозғалатын және жасырын тартқыштар». Еуропалық физикалық журналдың арнайы тақырыптары. 224 (8): 1421–1458. arXiv:1505.04729. дои:10.1140 / epjst / e2015-02470-3. S2CID 119227870.
- ^ Кузнецов Н.В .; Леонов Г.А .; Вагайцев В.И. (2010). «Чуаның жалпылама жүйесін тартудың оқшаулауының аналитикалық-сандық әдісі». IFAC материалдарының томдары. 43 (11): 29–33. дои:10.3182 / 20100826-3-TR-4016.00009.
- ^ Леонов Г.А .; Вагайцев В.И .; Кузнецов Н.В. (2011). «Жасырын Чуаның тартқыштарын оқшаулау» (PDF). Физика хаттары. 375 (23): 2230–2233. Бибкод:2011PHLA..375.2230L. дои:10.1016 / j.physleta.2011.04.037.
- ^ Леонов Г.А .; Вагайцев В.И .; Кузнецов Н.В. (2012). «Chua жүйелеріндегі жасырын аттрактор» (PDF). Physica D. 241 (18): 1482–1486. Бибкод:2012PhyD..241.1482L. дои:10.1016 / j.physd.2012.05.016.
- ^ а б Кузнецов, Н.В .; Леонов, Г.А .; Мокаев, Т.Н .; Прасад, А .; Шримали, MD (2018). «Рабинович жүйесінің ақырғы уақыты және жасырын тартқышы». Сызықты емес динамика. 92 (2): 267–285. arXiv:1504.04723. дои:10.1007 / s11071-018-4054-з. S2CID 54706479.
- ^ Кузнецов Н.В .; Леонов Г.А. (2014). «Динамикалық жүйелердегі жасырын аттракторлар: тепе-теңдіктері жоқ жүйелер, көп тұрақтылық және қатар өмір сүретін тартқыштар». IFAC жинағының томдары (IFAC Дүниежүзілік Конгресс материалдары). 47 (3): 5445–5454. дои:10.3182 / 20140824-6-ZA-1003.02501.
- ^ Кузнецов, Н.В .; Леонов, Г.А .; Юлдашев, М.В .; Юлдашев, Р.В. (2017). «Фазалы-бұғатталатын цикл тізбектерінің динамикалық модельдеріндегі жасырын тартқыштар: MATLAB және SPICE-де модельдеудің шектеулері». Сызықтық емес ғылымдағы байланыс және сандық модельдеу. 51: 39–49. Бибкод:2017CNSNS..51 ... 39K. дои:10.1016 / j.cnsns.2017.03.010.
- ^ Чен Г .; Кузнецов, Н.В .; Леонов, Г.А .; Мокаев, Т.Н. (2015). «Бір жолдағы жасырын аттракциондар: Глуховский-Должанский, Лоренц және Рабинович жүйелері». Халықаралық қолданбалы ғылымдар мен инженериядағы бифуркация және хаос журналы. 27 (8): өнер. сан. 1750115. arXiv:1705.06183. дои:10.1142 / S0218127417501152. S2CID 21425647.
